数据结构笔记

作者

主要学习视频是郝斌老师的《数据结构入门》，
其他学习资料以及参考均在文末列出。

目录

数据结构与算法概述

数据结构：我们如何把现实中大量而复杂的问题以特定的数据类型和特定的存储结构保存到主存储器（内存）中，以及在此基础上为实现某个功能（比如查找、删除、排序）而执行的相应操作，这个操作就是算法。

数据的存储分为两部分：个体的存储（可以忽略不计），个体关系的存储（核心）

数据结构 = 个体的存储 + 个体的关系存储
算法 = 对存储数据的操作

算法：解题的方法和步骤
衡量算法的标准：
1)时间复杂度：程序大概要执行的次数，而非执行的时间。(time complexity，这里time是次数的意思而不是时间)
2)空间复杂度：程序执行过程中大概所占用的最大内存空间。
3）难易程度：易于理解。
4） 健壮性：不能容易挂。（鲁棒性（robustness），源自robust这个词，其实就是健壮性）

狭义的算法跟数据存储有关； 广义的算法跟数据存储无关。

泛型： 同一种逻辑结构，无论其内部的物理存储结构是什么样子，都可以对它执行相同的操作。

程序 = 数据的存储 + 数据的操作 + 可以被计算机执行的语言

预备知识

指针

见c笔记。
一般定义指针：p q r

结构体

//定义结构体
 struct Student
 {
     int sid;
     char name[200];
     int age;
 };

image
image
通常使用第二种方式，可以少定义一些变量名
image

malloc()动态分配内存

image
HEU}IWEHPM89Q$K3XLL1QVV
动态分配内存的好处：
1，可以在程序运行过程中，根据用户不同需求动态地分配内存；2，可以在程序运行过程中释放
注意，malloc()动态分配的内存必须通过free()释放。没有释放的话，即使函数终止，内存也还存在，整个程序彻底终止的时候才可能释放。

跨函数使用内存

image
image
image
image
答案：C
一个星的指针存放的是变量的地址。两颗星的指针存放的是指针的地址

typedef

例1：
W94LSAT0%D`Y
C777LRM6B5NWI2K~`)D%J6M
例2：
2TWMA(X(S{{L
例3：两个别名，* 和无 \
image
星号置于两者之间，从前往后看是“的指针”从后往前看是“的指向”。

线性结构

可以用一条直线把所有节点串起来

连续存储：数组

什么叫数组：元素类型相同，大小相等

数组的优缺点
优点：存取速度很快
缺点：事先必须知道数组的长度；插入删除元素很慢；空间通常有限制；需要大块连续的内存块

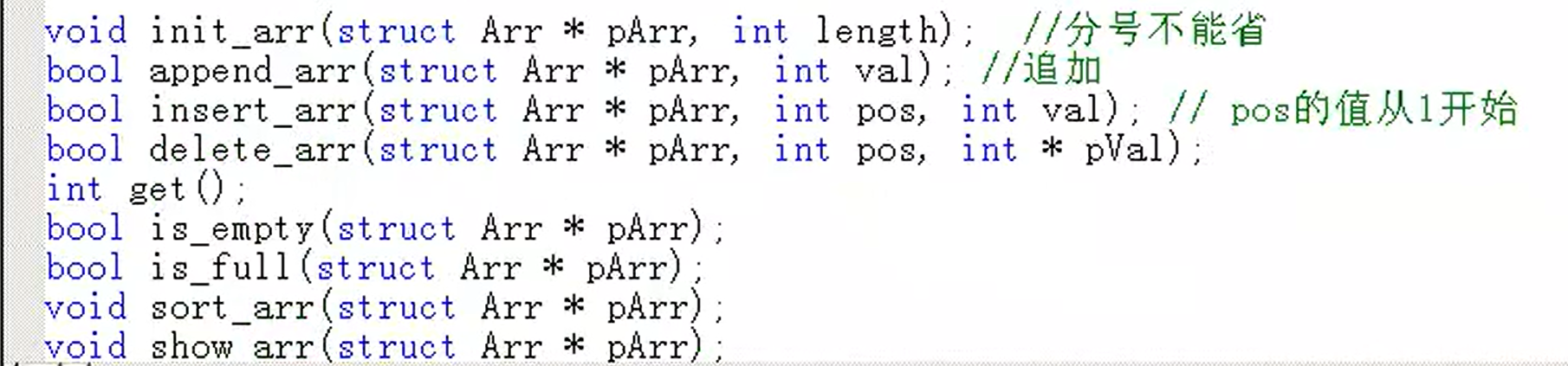
确定一个数组需要几个参数（如果希望通过一个函数来对数组进行处理，我们至少需要接收链表的哪些参数）
1）首地址
2）长度
3）有效元素的个数

<code>G_15Q)(1EO4</code>$~HPMU3I7S
N
$
7
L
$

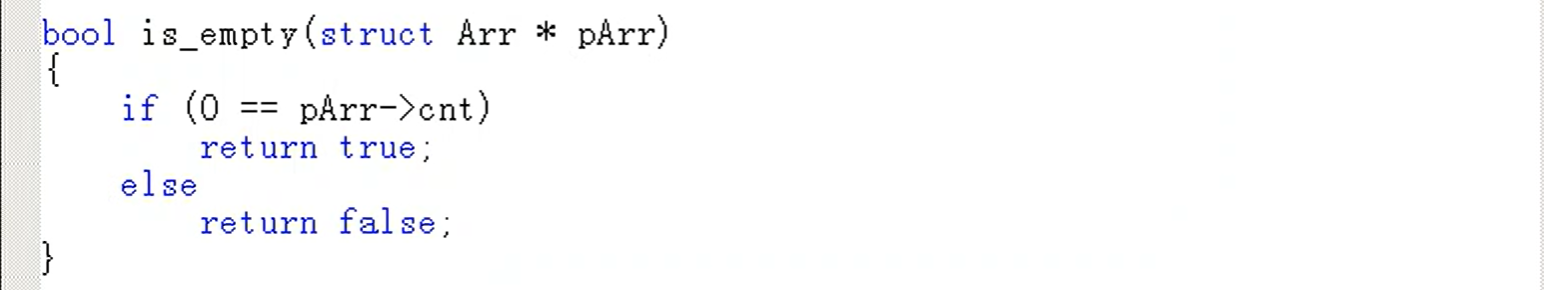
(_K{NZ1M5S9@_H}%GF(3M)L
T
VKCG7F0X_D7QT2O(P81BDG1
G85)}4WU3)~H%8W8C0LG4NF
4
%

JZ8Z(QYZ5$SN74$WE_~RGHO
5A%K52ZCRQZLMZ}Y7CFM_HR

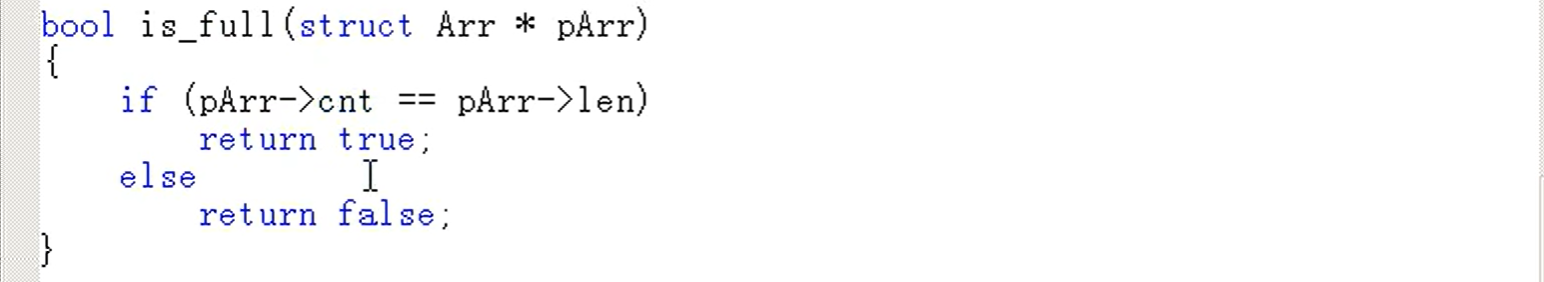
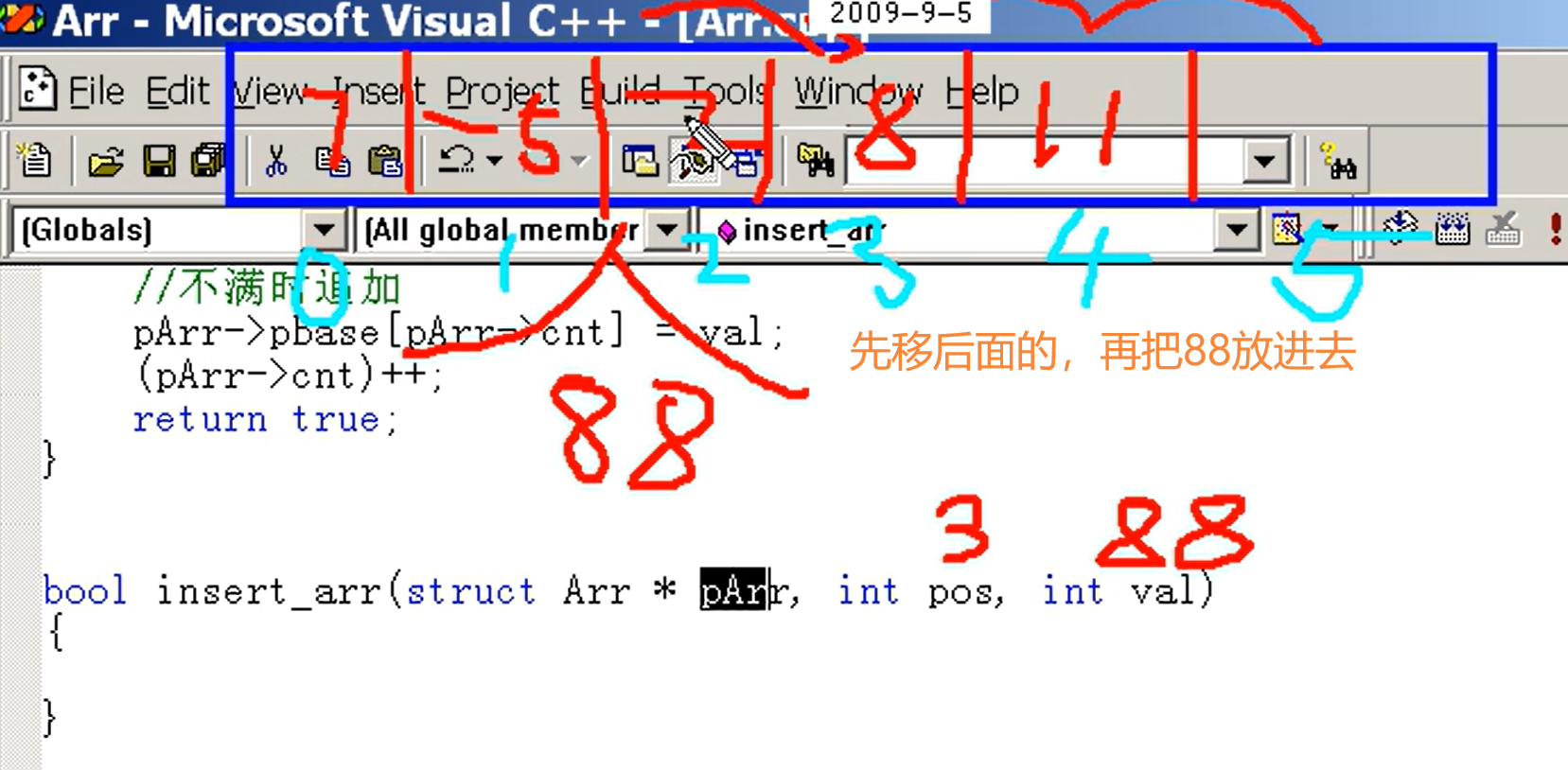
离散结构：链表

概念

定义
（1）n个节点离散分配，（2）彼此通过指针相连，（3）每个节点只有一个前驱节点同时每个节点只有一个后续节点，（4）首节点没有前驱节点，尾节点没有后续节点。

专业术语
1）首节点：存放第一个有效数据的节点。
2）尾节点：存放最后一个有效数据的节点。
3）头结点：位于首节点之前的一个节点，头结点并不存放有效的数据，加头结点的目的主要是为了方便对链表的操作。头节点的数据类型和首节点类型一样。
4）头指针：指向头结点的指针变量（不是指向首节点，不然就叫“首指针”了），是头节点的地址。
5）尾指针：指向尾节点的指针变量。
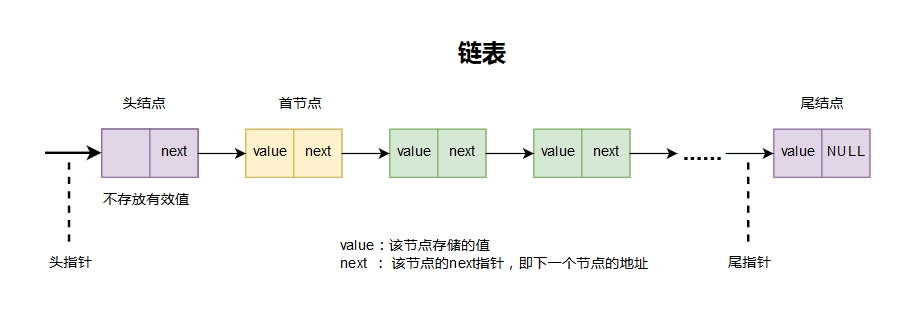
image

确定一个链表需要几个参数（如果希望通过一个函数来对链表进行处理，我们至少需要接收链表的哪些参数）：只需要一个头指针参数，因为我们通过头指针可以推算出链表的其他所有信息。不用头节点是因为不同链表头节点不同，没法确定数据类型，没法确定形参类型。

每个链表节点的数据类型如何表示
image

分类
1）单链表：每一个节点只有一个指针域
2）双链表：每一个节点有两个指针域
image
3）循环链表：能通过任何一个节点找到其他所有的节点。循环链表属于双链表的一种特殊形式，即循环链表是双链表的一个子集。
4）非循环链表：不能通过任何一个节点找到其他所有的节点

链表的优缺点
优点：空间没有限制，插入和删除元素很快
缺点：存取速度很慢

操作（非循环单链表）

算法
遍历，查找，清空，销毁，求长度，排序，删除节点，插入节点

插入

WIJQ
image
K80F
D

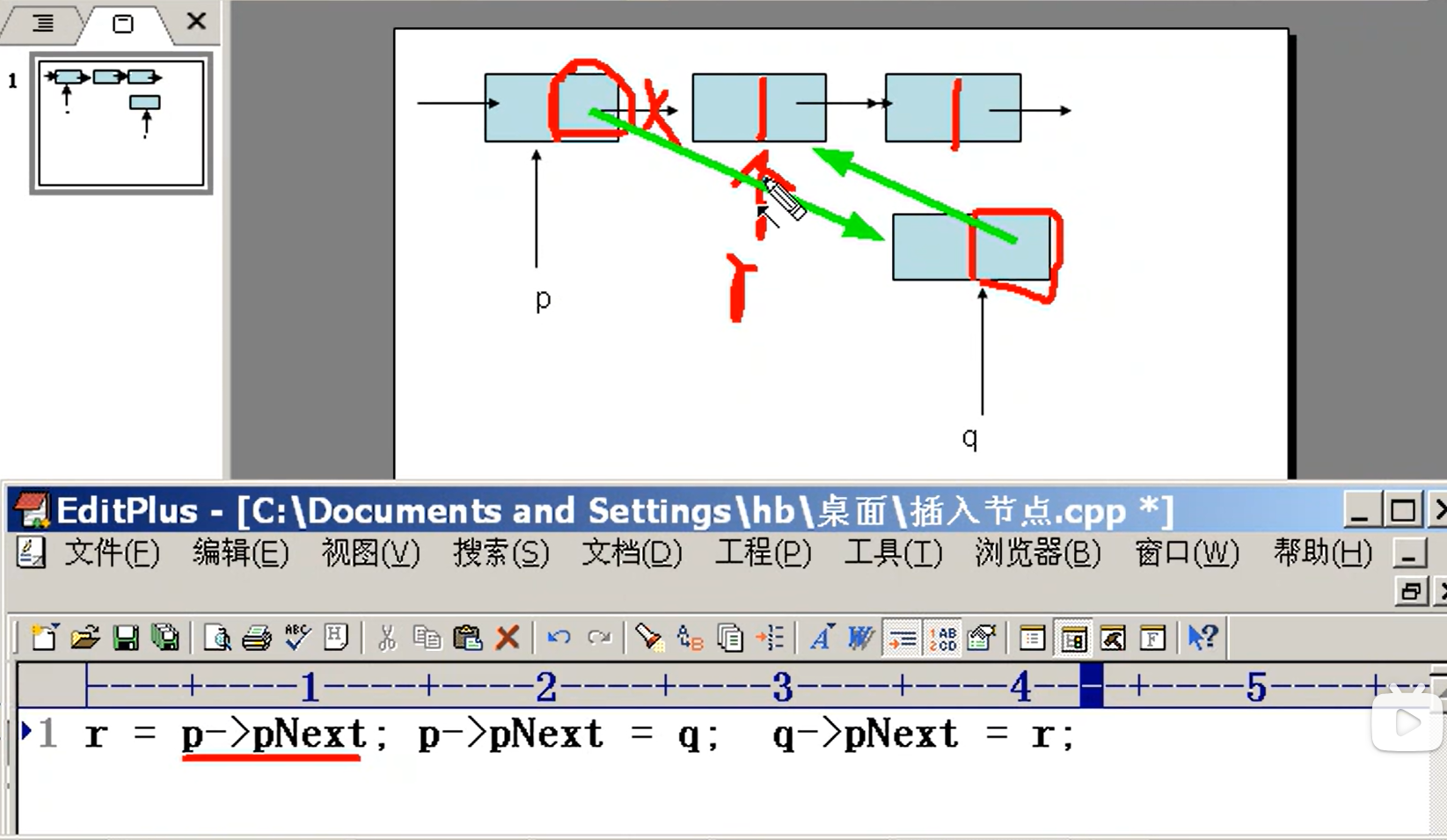
删除


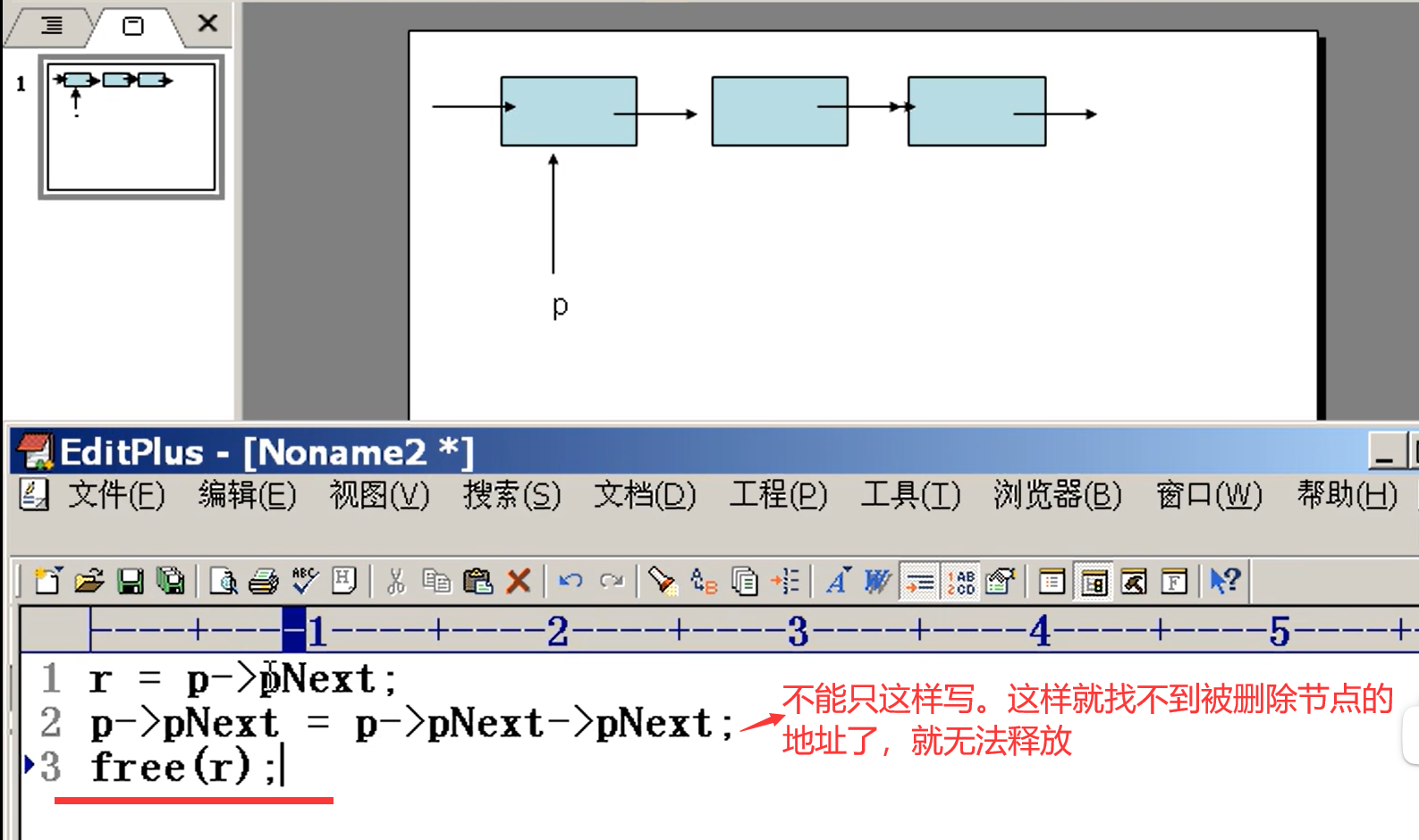
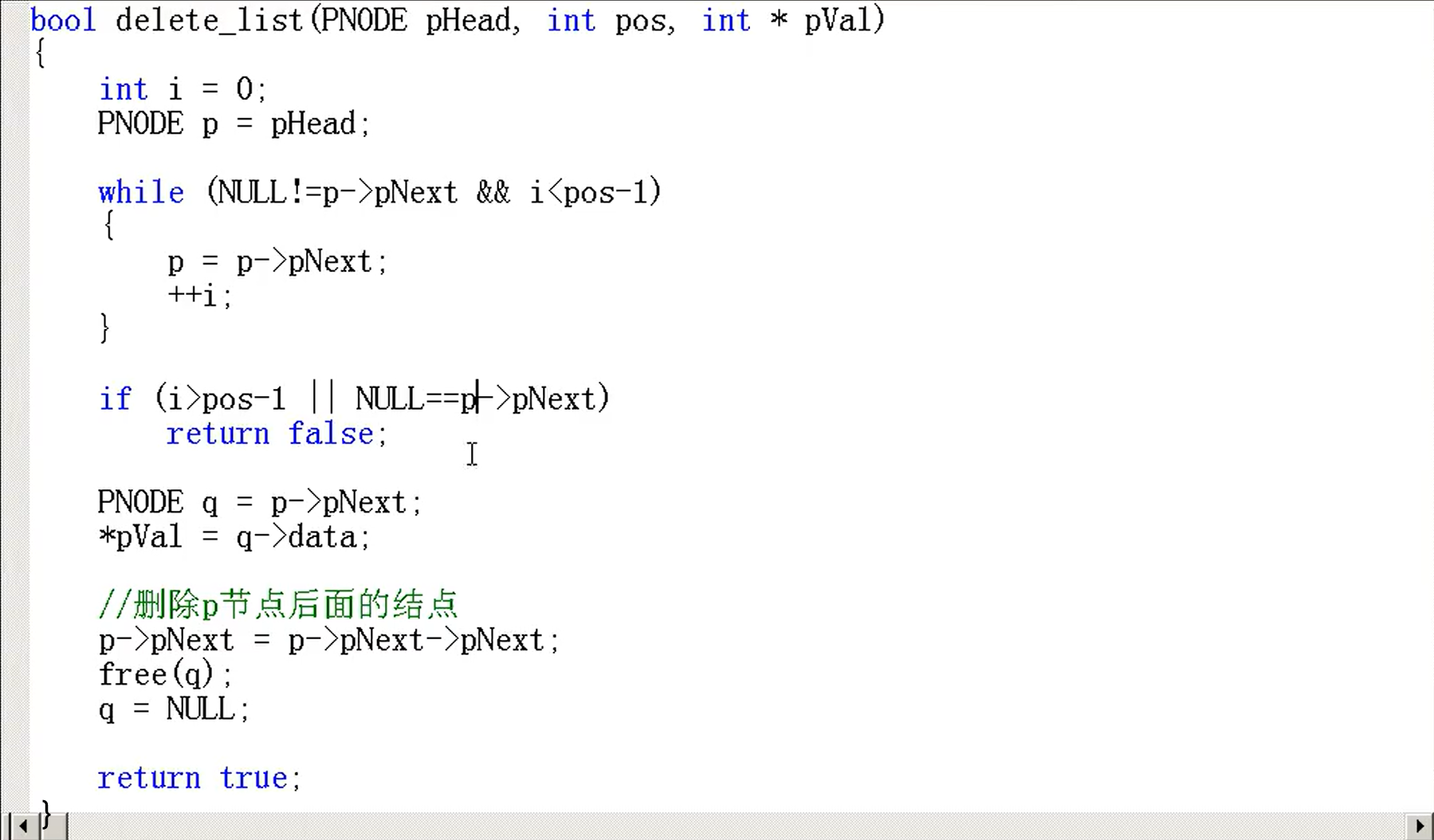
image
想要删除第pos个节点，找到pos-1，删除pos-1后面一个(第pos个)
（这个代码健壮性很好）

创建&遍历

0
G3Z9G
GS248R8L29
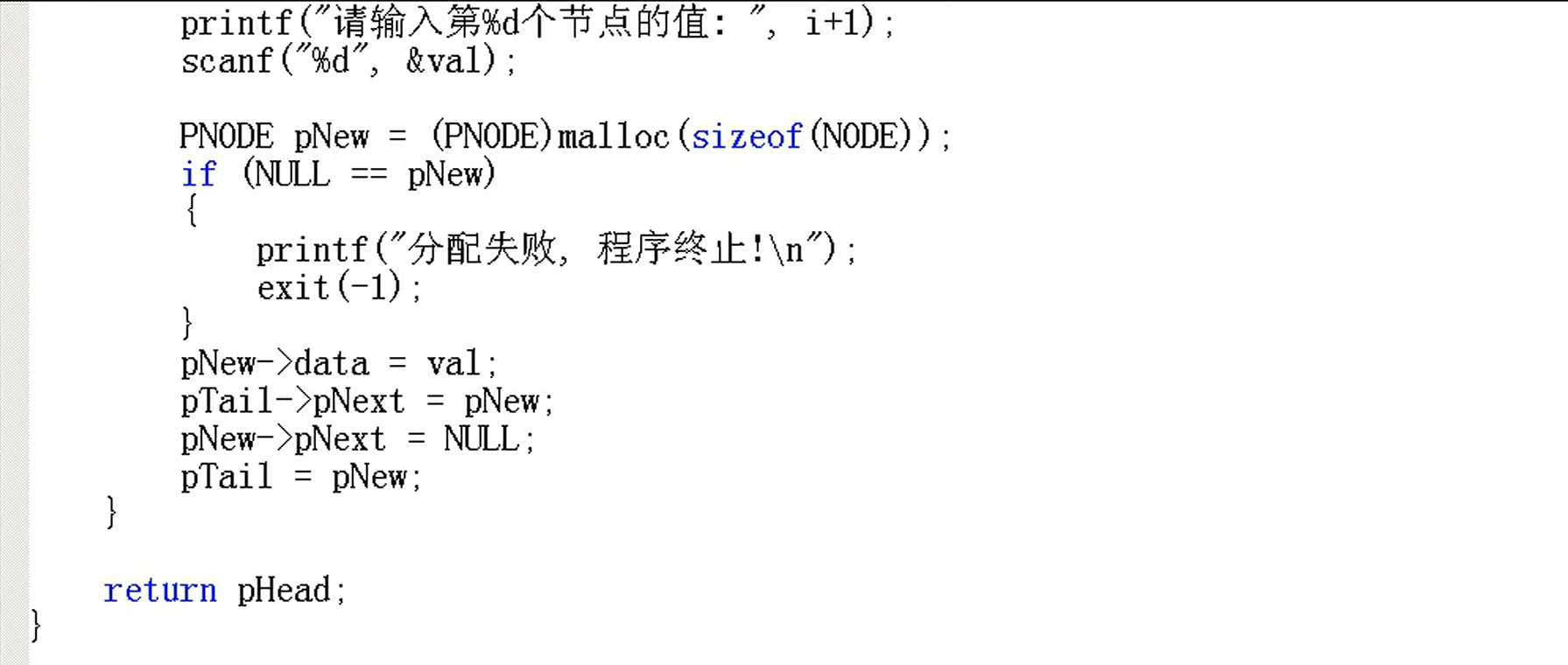
@ODRBTD6L
%TE$OW1@ID

判断链表是否为空

image
image

求链表长度

image

通过链表排序算法的表示

选择排序。狭义上来说与数组的选择排序不一样；从广义上来说，都是线性结构，算法与数组的选择排序一样
image

线性结构的应用一：栈

概念

定义：一种可以实现“先进后出”的存储结构（或称作存储方式），类似于箱子。
静态内存分配在栈中，动态内存分配在堆中
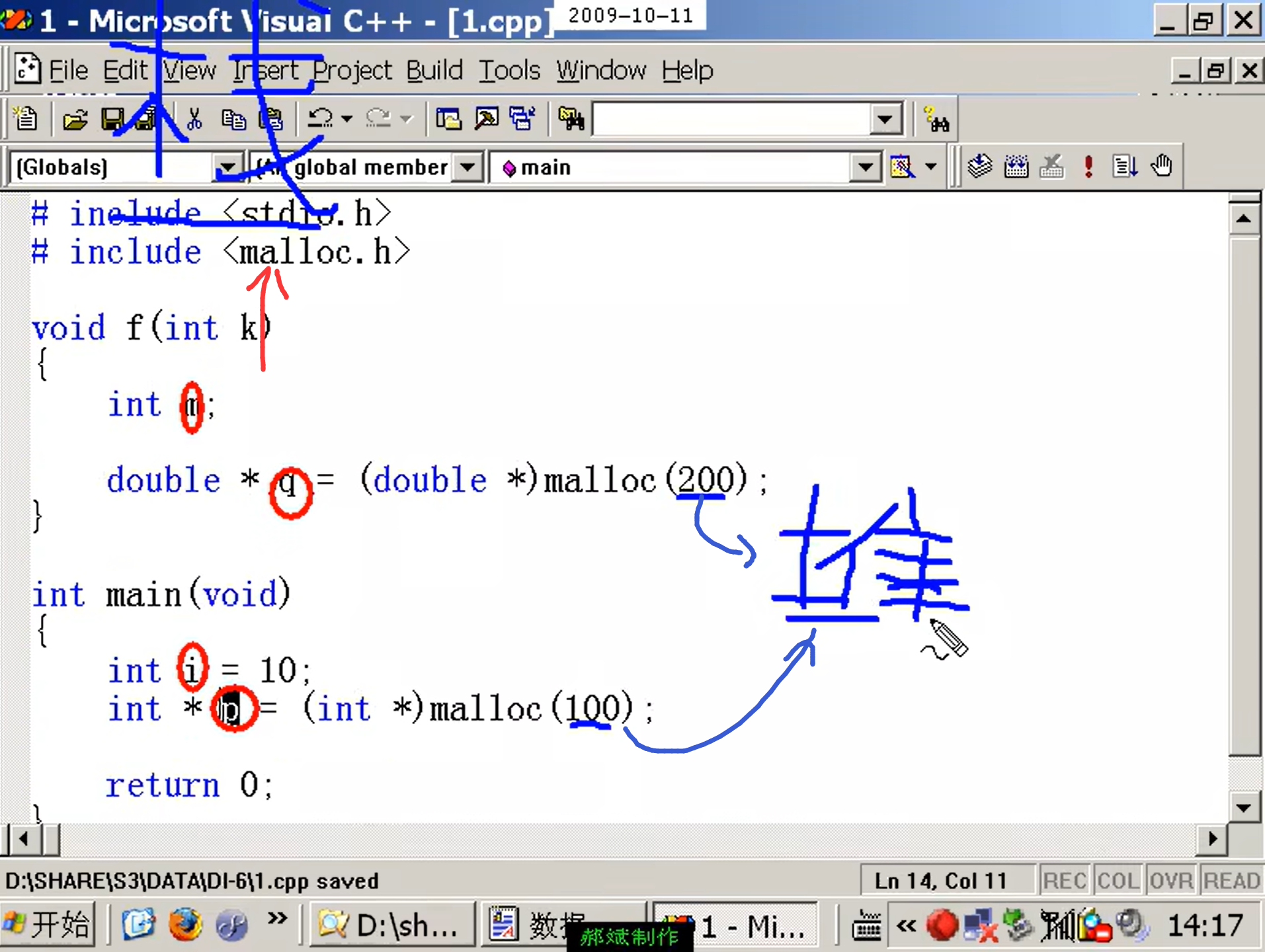
image

分类

1）静态栈：以数组为基本内核
2）动态栈：以链表为基本内核

算法

  • 压栈（入栈）
  • 出栈

动态栈，或说用链表实现的栈，本质是一个操作受限的链表（只能从一个口进出，另一个口封死(像箱子)）。

伪算法
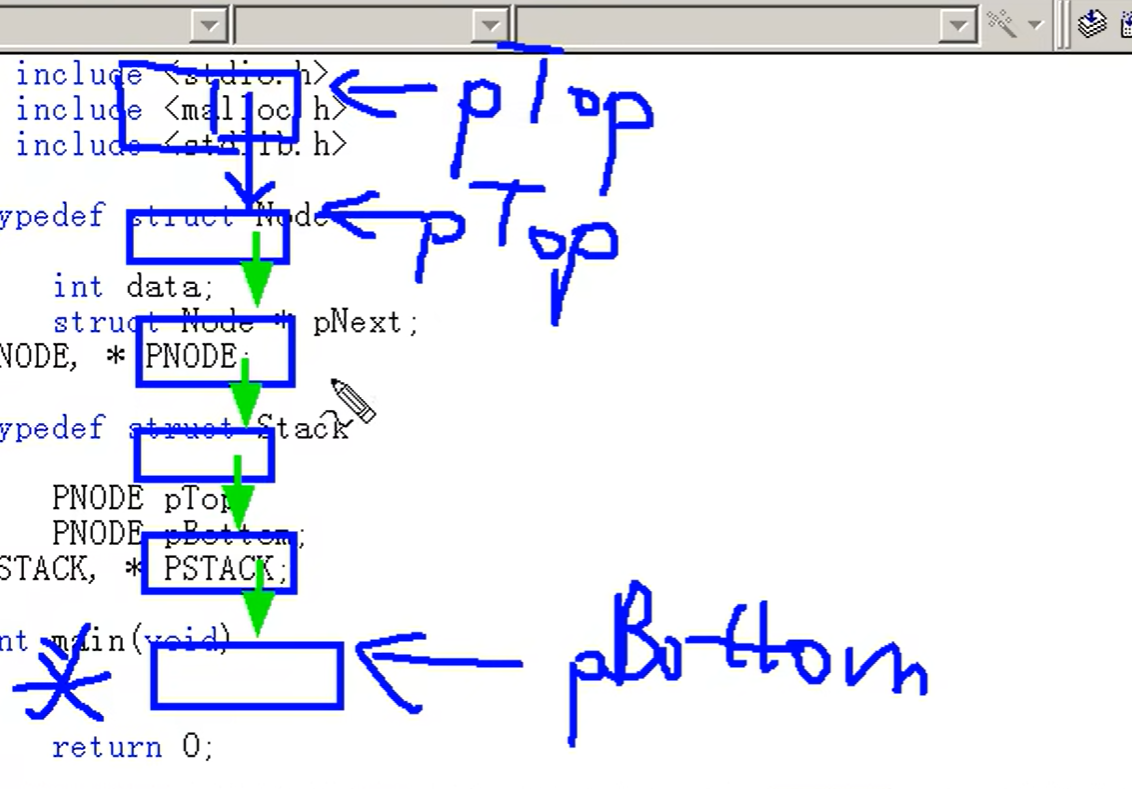imagepB指向最后一个有效元素的下面一个元素，即无实际值的头节点。这里头节点在最“底”下
删除元素时pT下移
判断栈空：pT==pB
链式栈不存在满的问题

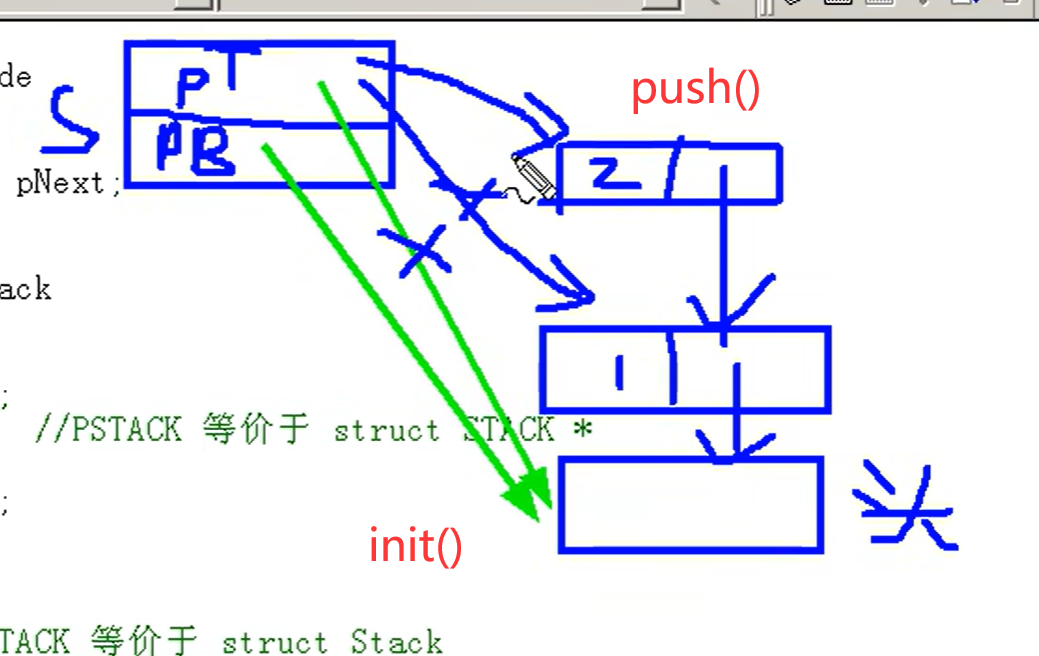
image
添加元素 push()：
在最上面添加一个元素

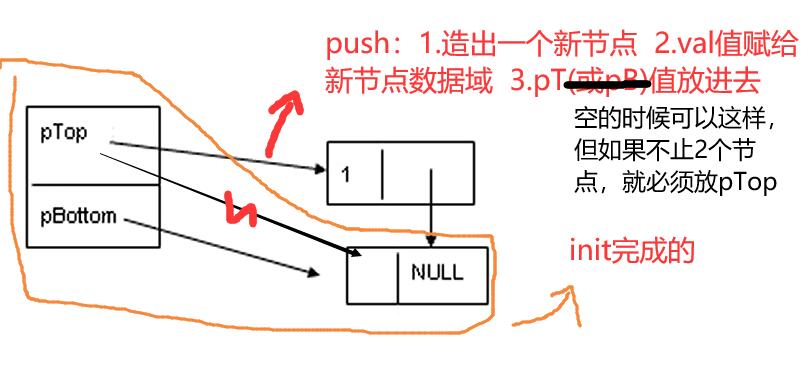
遍历元素 traverse()：
从上开始输出
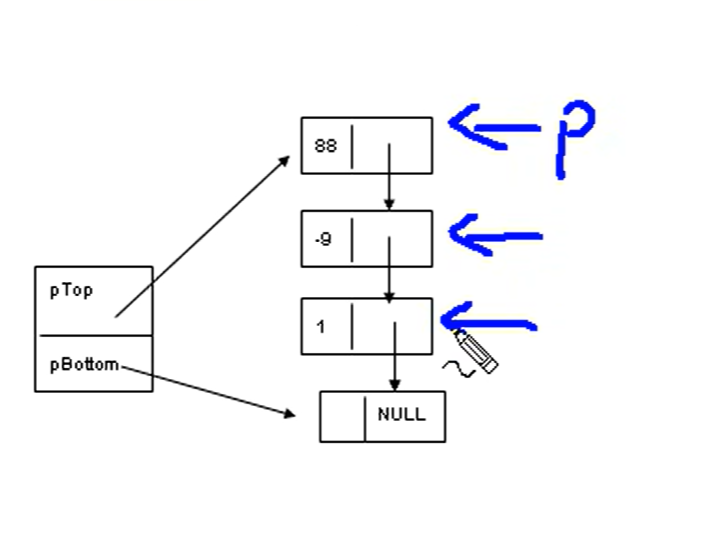
image
出栈 pop()：
删除最上面一个元素
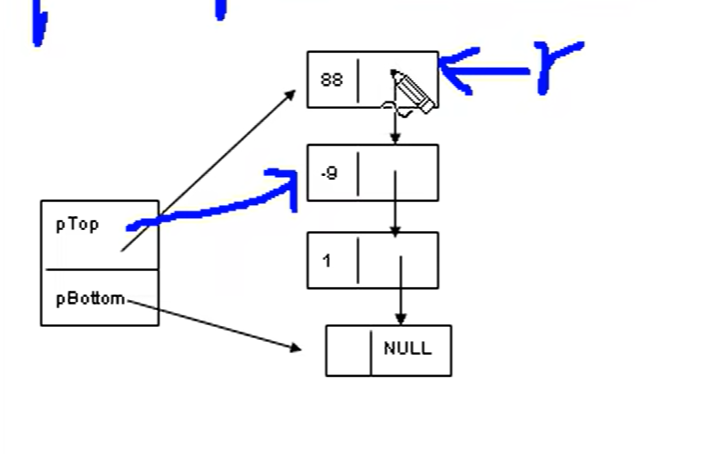
image
清空 clear()：
注意，不是销毁（destroy）。清空只是删除数据，框架还在；销毁是什么都没了。类似数据库中truncate（只删数据）和drop（删整个表）。
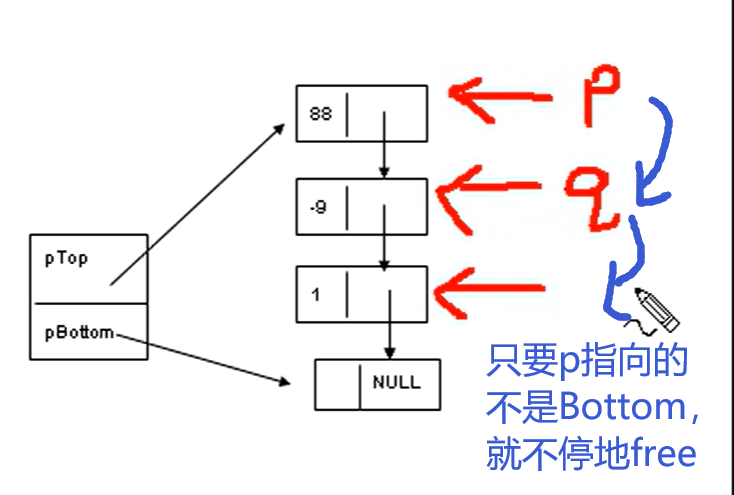
image

代码
N044KAM5JJL4
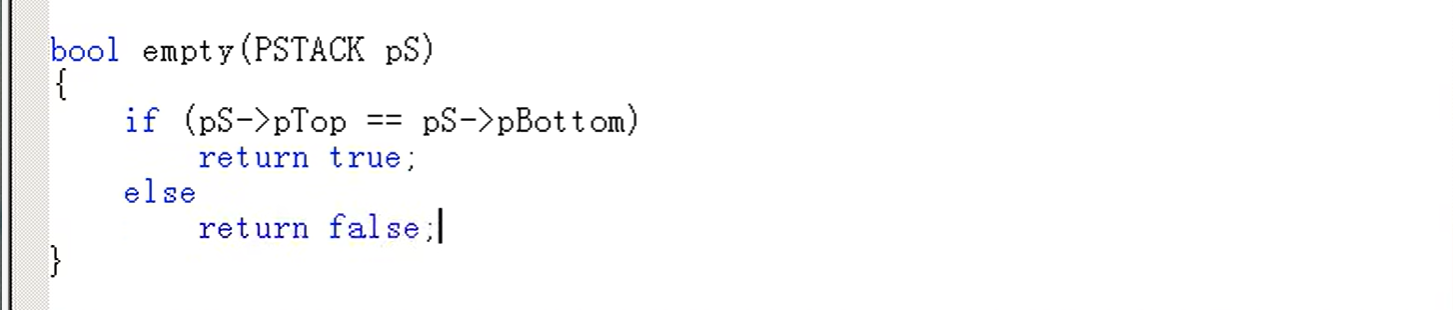
image
C{~SBK%67C{H{BJBDSUEEP@H3N%%EMHFX0C
07GV97311
2KDIG
B0W6
image
E%ESF7S
CR55D

应用

1）函数调用。 f调用g，g调用k； 执行的时候，先执行k，再g再f
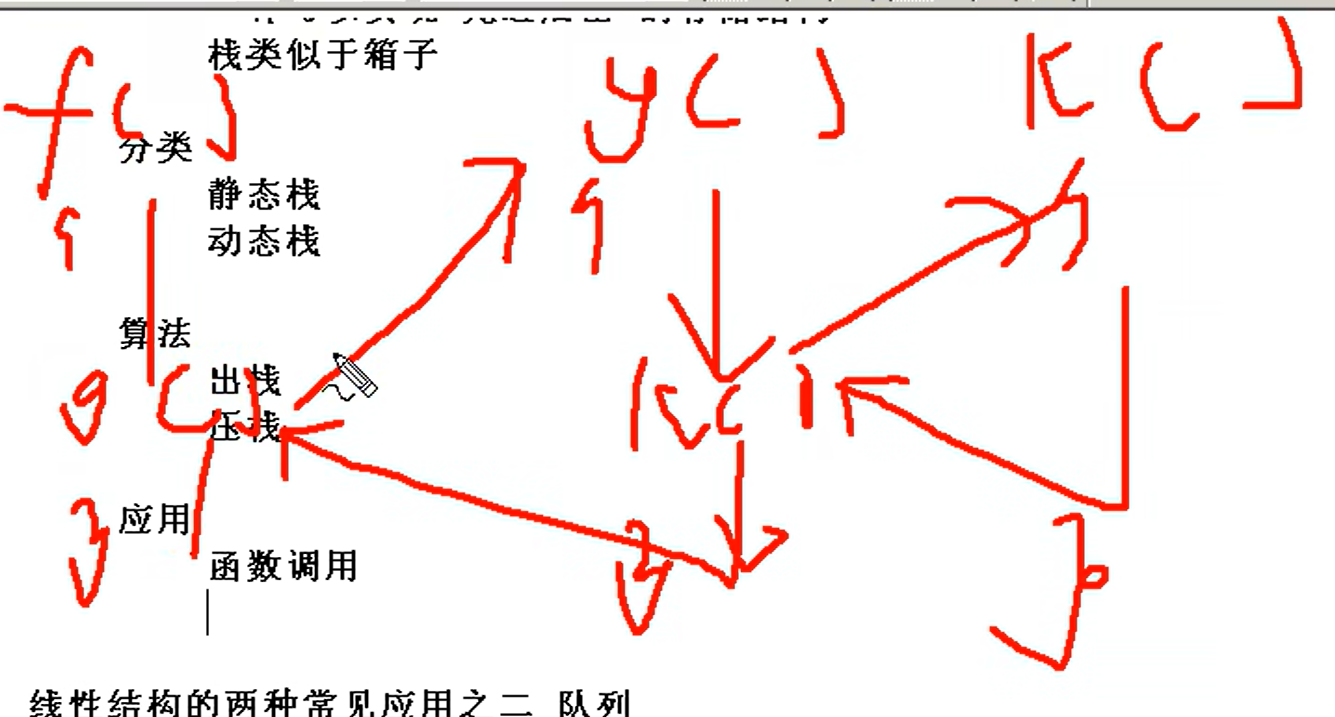
image
2）中断
3）表达式求值 （两个栈可以编写计算器，运算符优先级）
4）内存分配
5）缓冲处理
6）迷宫

线性结构的应用二：队列

定义

队列是一种够可以实现“先进先出”的数据结构。类似于排队
只允许一端出，一端入，且不能对中间元素操作。

和栈区别：栈是一端，队列是两端。
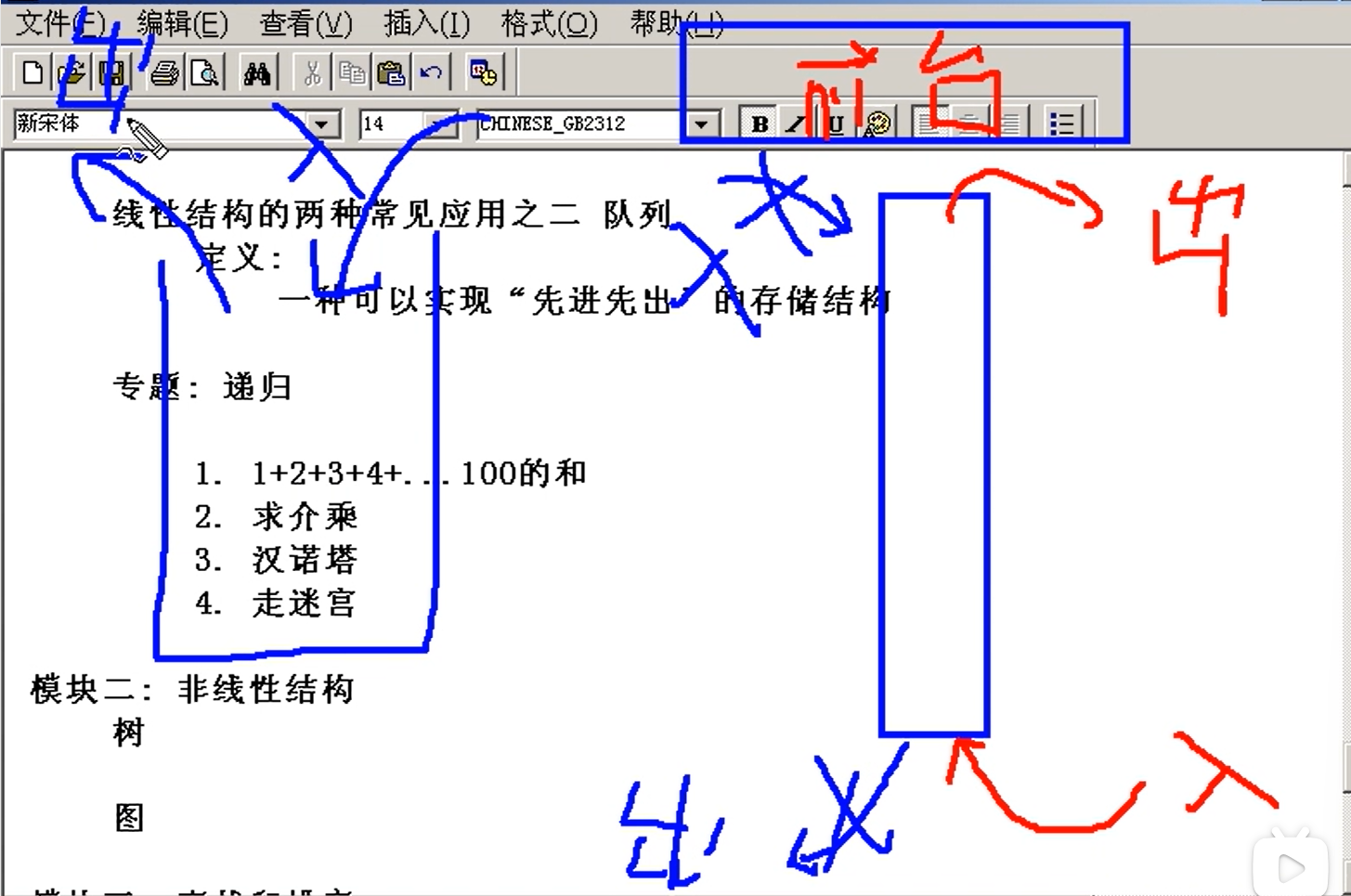
image

分类

1）链式队列：用链表实现
2）静态队列：用数组实现，通常都必须是循环队列

操作

  • 入队（类似压栈）
  • 出队（类似出栈）
    需要两个参数来确定队列（为和链表区分开来）：front（头部），rear（尾部）

链式队列：
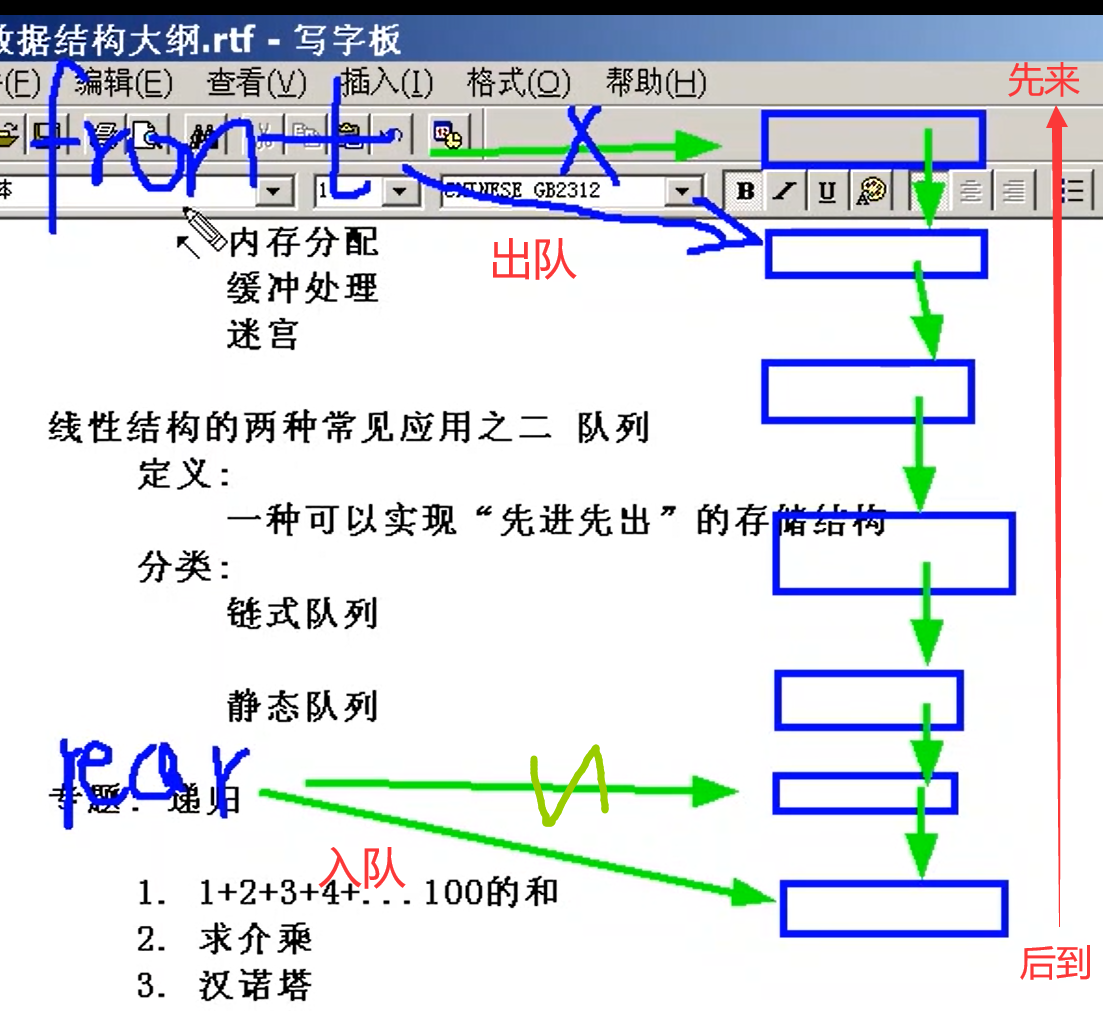
image
静态队列：
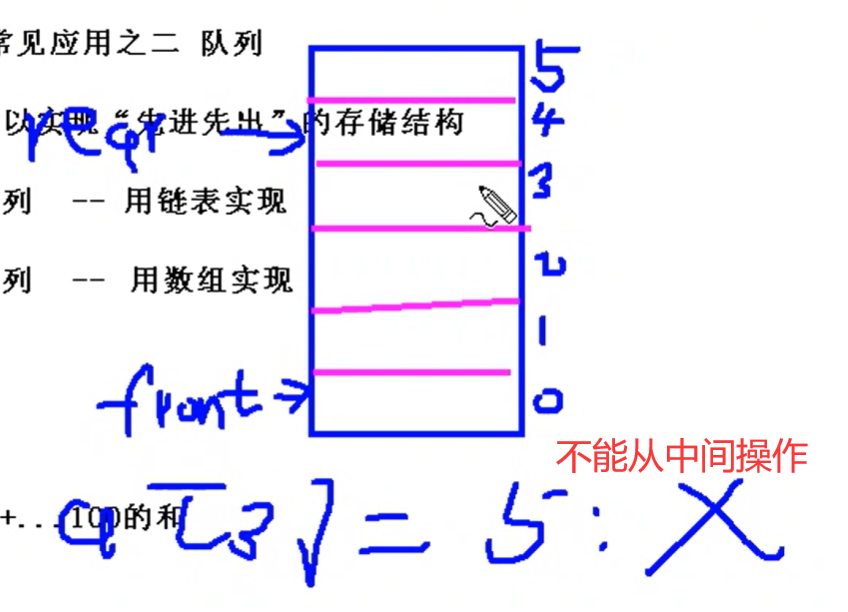
image

循环队列

循环队列需要几个参数来确定

需要两个参数来确定队列，front 和 rear
队列非空时（每种场合下不一样），f指向第一个元素，r指向最后一个元素的后一个
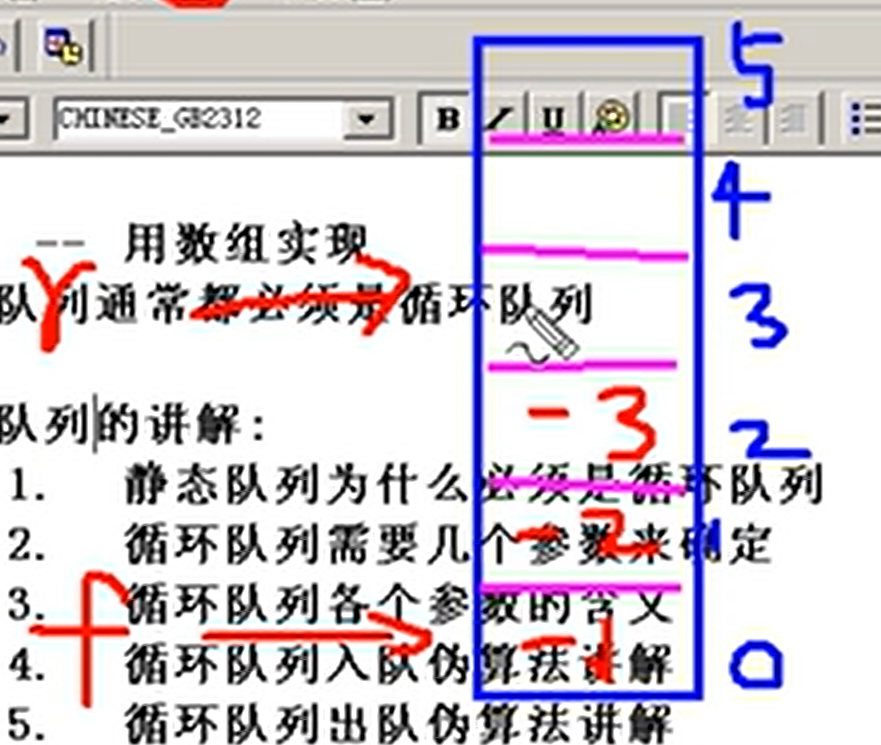
image

循环队列各个参数的含义

有三种场合：
1）队列初始化：front和rear的值都是0
2）队列非空：front代表的是队列的第一个元素，rear代表的是队列的最后一个有效元素的下一个位置
3）队列空：front和rear的值相等，但不一定是0

其实循环队列不能说头尾，只能说先进先出。f和r的下标大小不定。
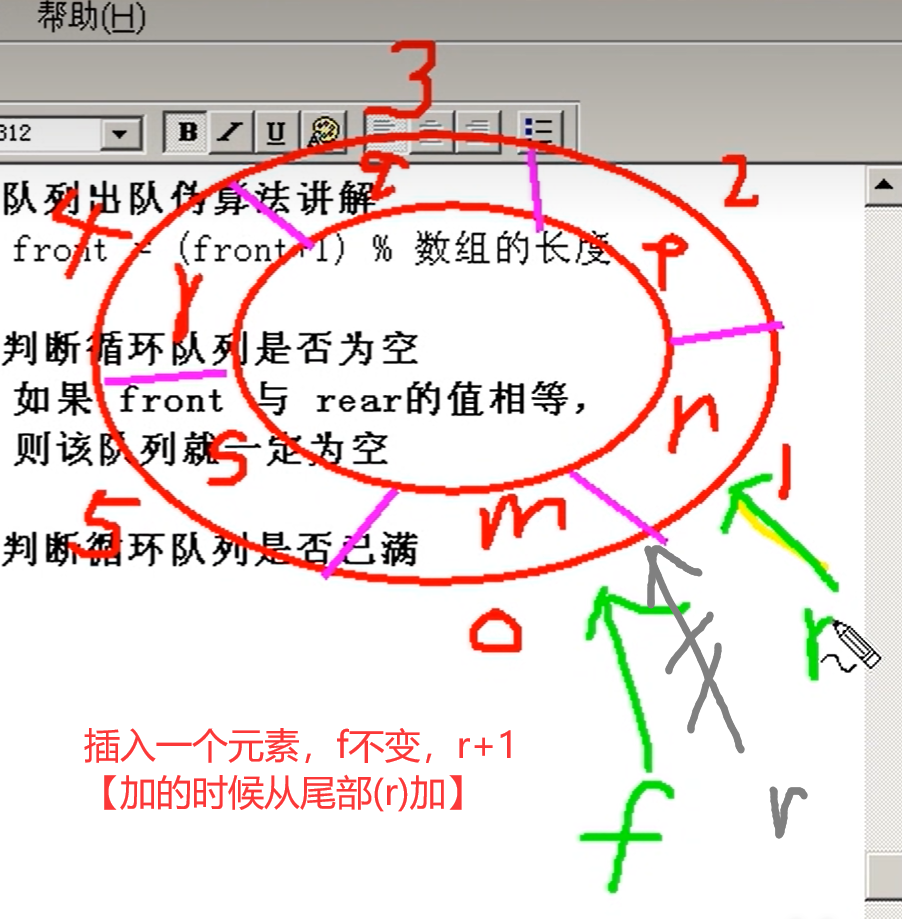
$DCFPAN1
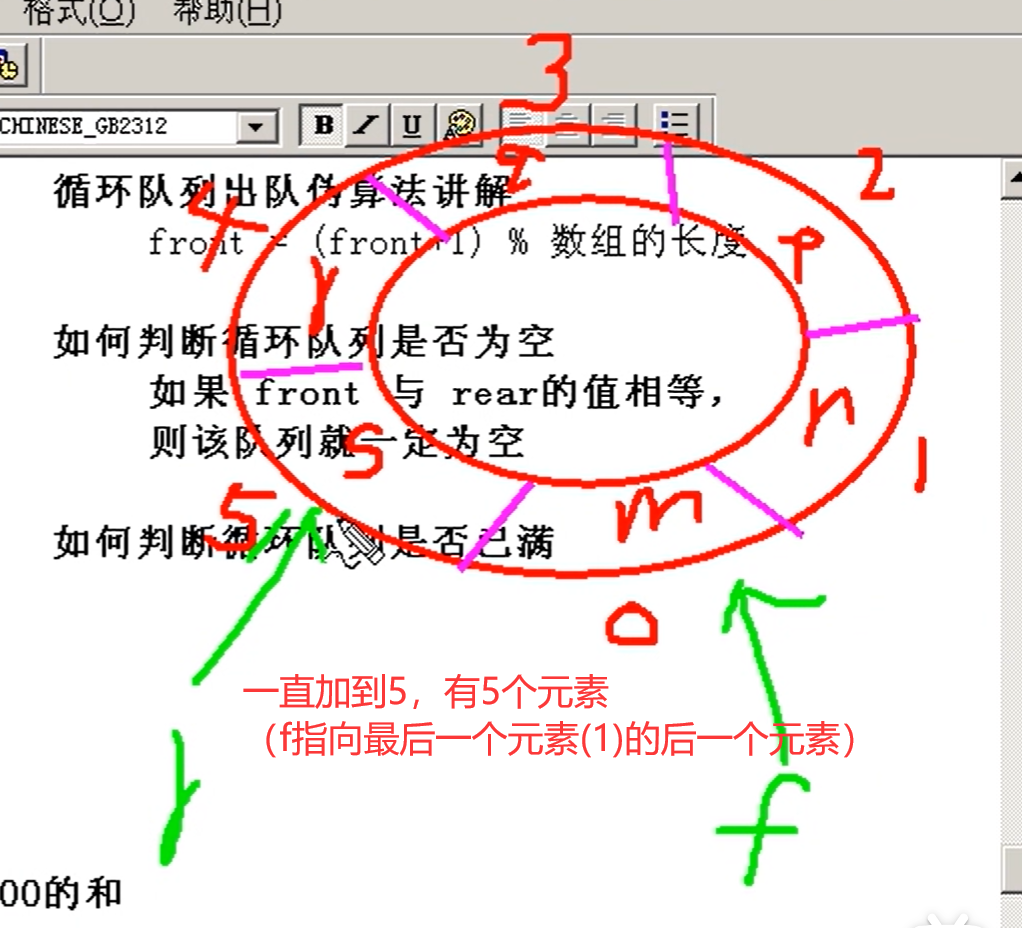
V09LRD87GL
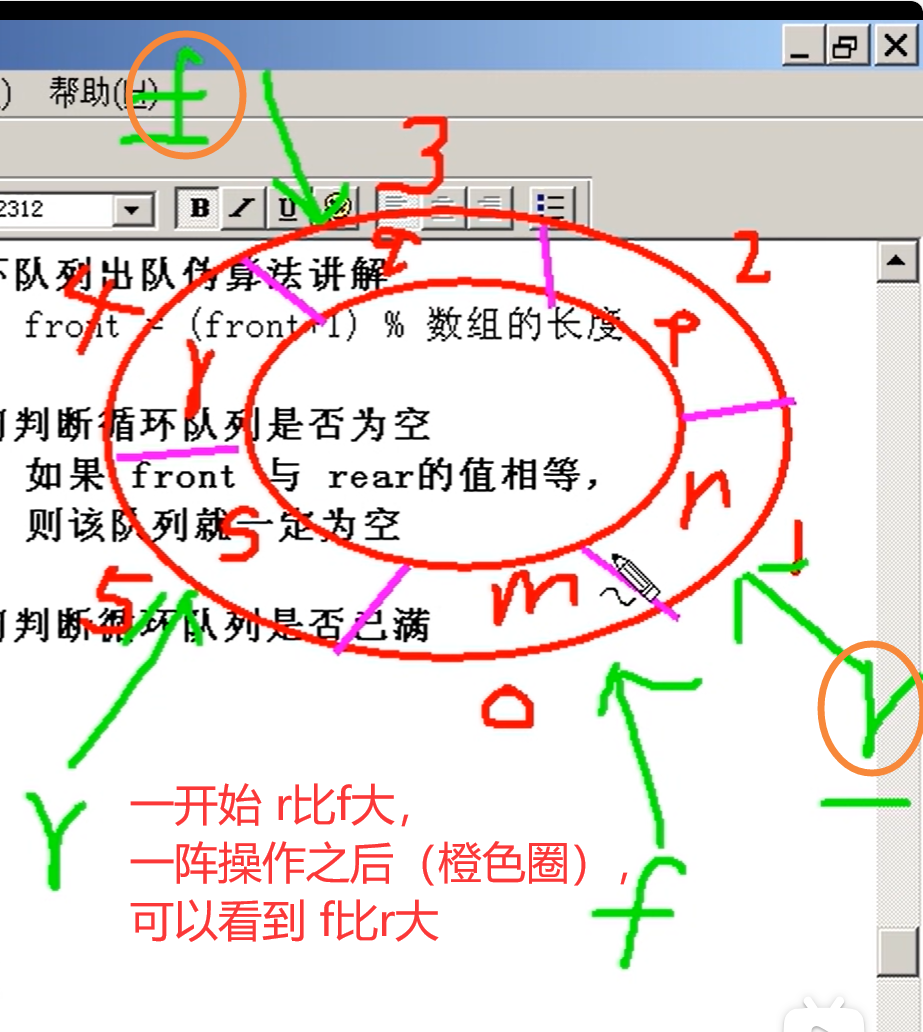
7PI9L

静态队列为什么必须是循环队列

因为是用数组实现的而不是链表
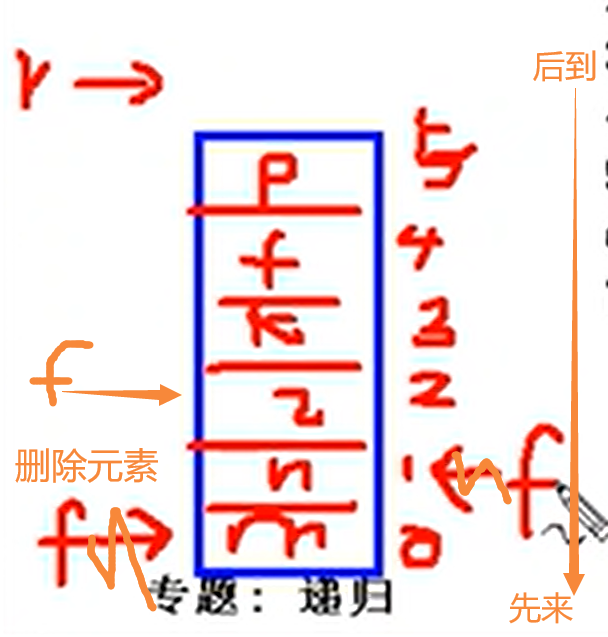
image
要删除的时候f指向后一个元素（出队，f++），如果不是循环队列（传统的数组），被删元素所在的那些位置将永远不被使用，也就是说，队列的前面会空出位置，这些位置就浪费了。
要添加的时候r往后一个（入队，r++），也是同理。
若是循环队列，在添加元素的时候，如果rear已经到顶部，rear可以从上面跳到下面接上去。
循环队列添加元素：
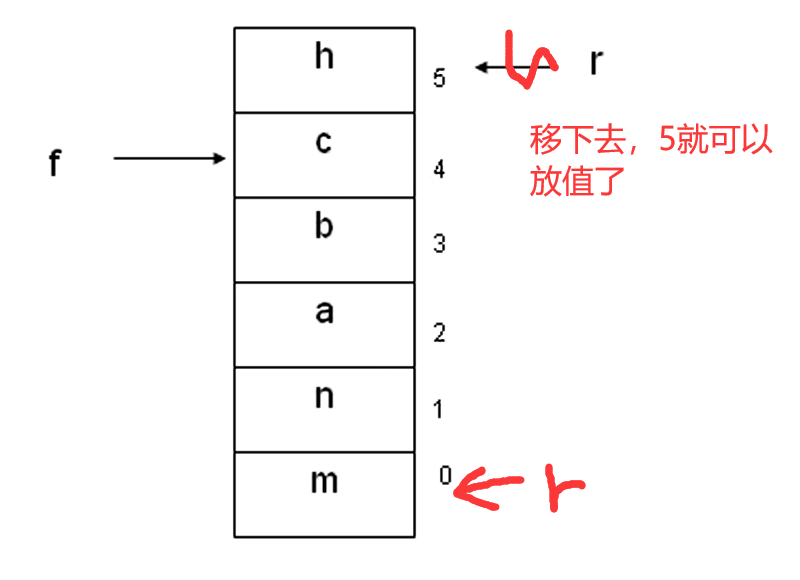
image
循环队列删除元素：
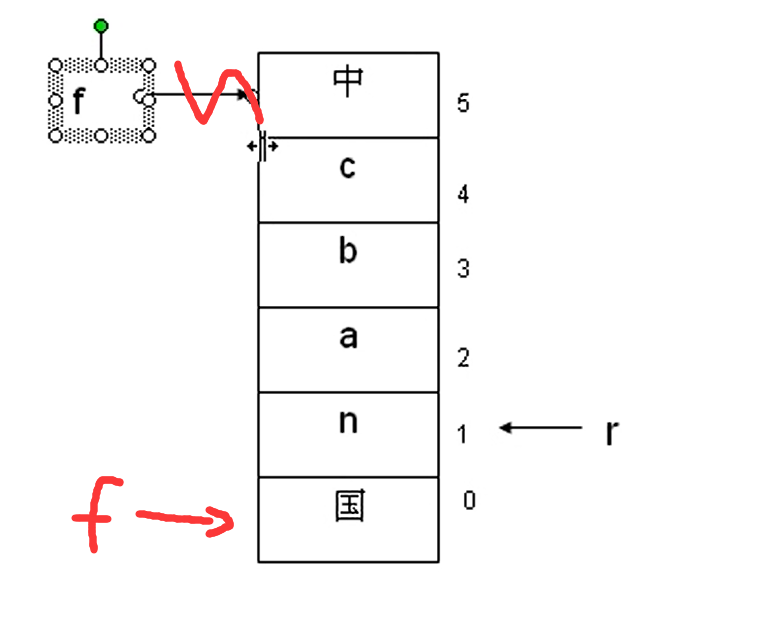
image
若是链式队列，本质是链表，不用担心以上的问题。

循环队列入队伪算法

从尾部入。
步骤：

  1. 将值存入rear所代表的位置
  2. rear = (rear + 1) % 数组的长度
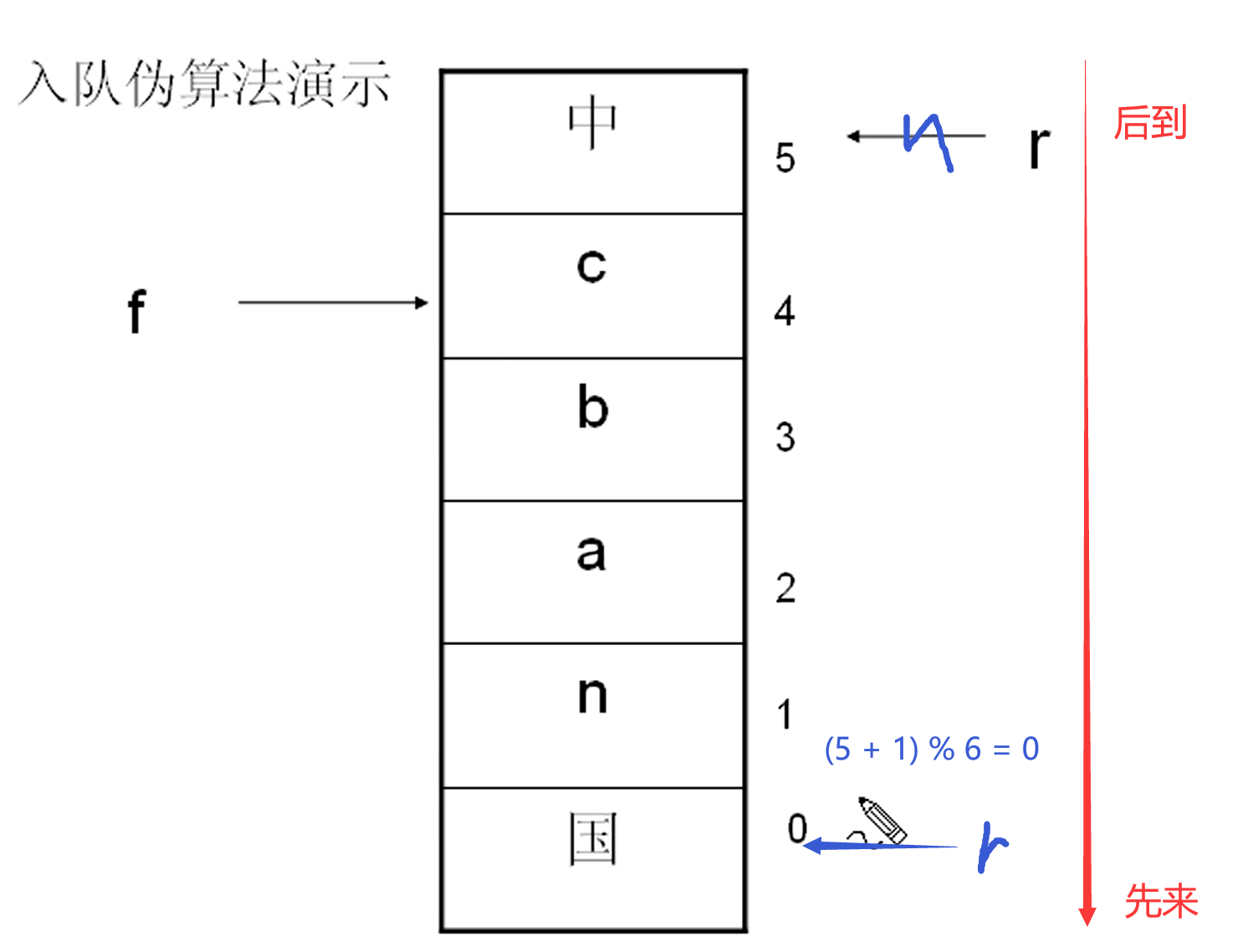
    image

循环队列出队伪算法

front = (front + 1) % 数组的长度
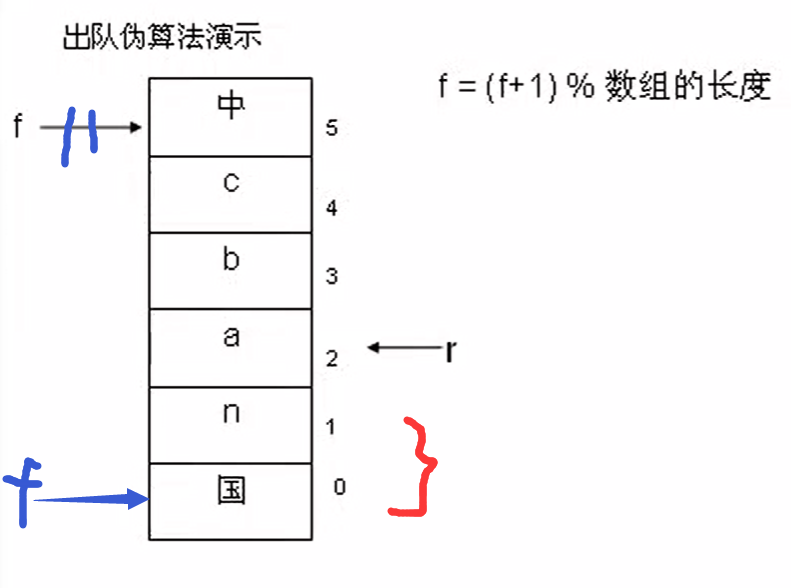
image
注意：入队，出队都是加

如何判断循环队列是否为空

if (front == rear)

如何判断循环队列是否已满

判断 r 的下一个位置是否是 f
两种方法：
1）if ((rear + 1 % 数组的长度) == front)
2）元素个数 = 数组长度 - 1
队列里有一个元素一定不能使用，“头节点”
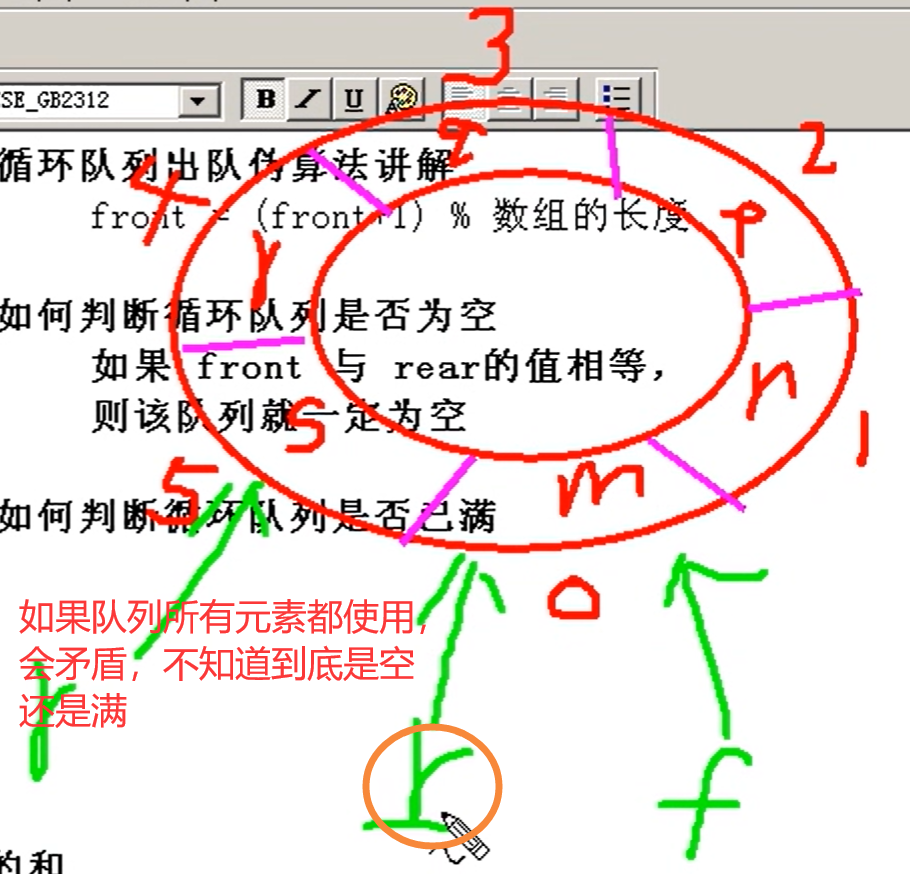
image
有几个元素：从 f 开始数（包括 f)，往大下标走，到 r 结束（不包括r）

代码

OTQ
image
~R
QK
1
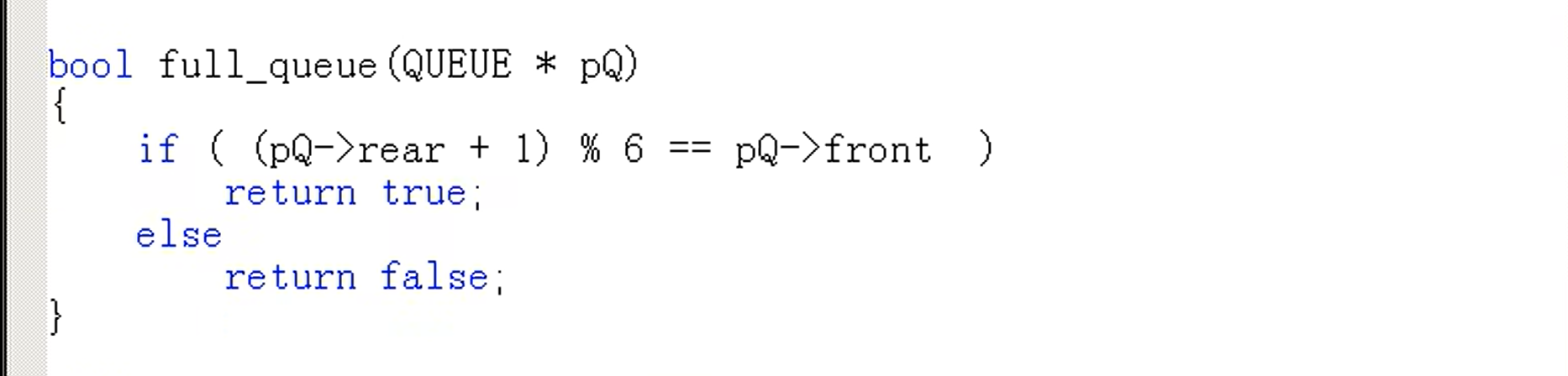
FVIZR
A2
GE
Q5
EUW

应用

所有和时间有关的操作都有队列的影子，需要先进先执行的就用队列。
如OS里“等待队列”、线程中的“执行队列”、“执行队列”。

递归

递归概念

递归的定义
一个函数直接或间接地调用自己

递归要满足的三个条件

  1. 递归必须有一个明确的终止条件
  2. 该函数处理的问题规模必须在递减
  3. 这个转化必须是可解的

如何写递归代码
逆向思维，不要太深究细节操作，千万不要去企图理解递归的每个步骤，拆成小问题就行。
只要：

  1. 写程序告诉电脑“如何分解一个问题”
  2. 写程序告诉电脑“当该问题分解到最简时如何处理”

循环和递归
递归：好理解，运行速度慢（因为要调用函数），存储空间大
循环：不好理解，运行速度快，存储空间小
理论上来说，所有的循环都可以用递归来解决，但用递归能解决的用循环不一定能解决。

递归的例子

1）求阶乘
image
2）求1~n的和
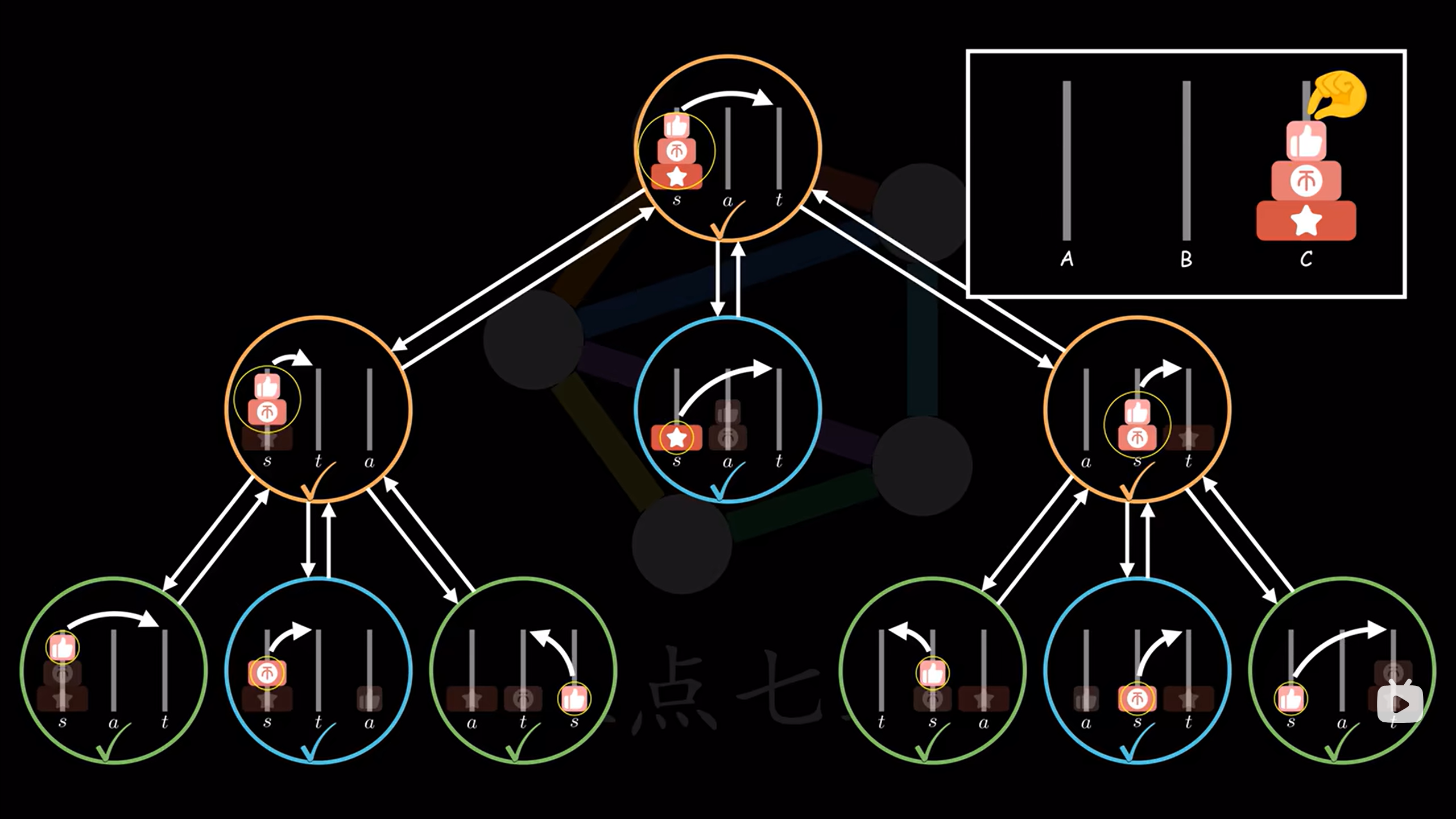
3）汉诺塔：（学会了可以写一下Leetcode 面试题 08.06. 汉诺塔问题）
在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，将所有盘子从第一根柱子移到最后一根柱子。

如何把大象放到冰箱里？开门，放进去，关门。
在汉诺塔中是：先将（n-1）个从初始柱（A)通过目标柱(C)到中间柱(B)，将最后一个移动到目标柱(C)，再将前（n-1）个运到目标柱（C）。
那怎么把（n-1）个盘子运到中间柱？将C柱当作中间柱，再重复上述过程就可以了。

伪算法：
OEDD
WDH

伪代码：

# include <stdio.h>

void hanoi(int n,char A, char B,char C){
    if (1 == n){
        move(A, C);
        printf("编号为%d的盘子：%c-->%c\n", n, A, C);
    }
    else{
        hanoi(n - 1, A, C, B);
        move(A, C);
        printf("编号为%d的盘子：%c-->%c\n", n, A, C);
        hanoi(n - 1, B, A, C);
      //上面的(n-1)个:当前柱 -> 中转柱 (让开)
      //我:当前柱 -> 目标柱（过去）
      //那(n-1)个:中转柱 -> 目标柱(过来)
    }
}

int main(void){
    //柱子编号
    char ch1 = 'A';
    char ch2 = 'B';
    char ch3 = 'C'; //目标柱

    //盘子个数
    int n;
    printf("请输入盘子的个数：");
    scanf("%d", &n);

    hanoi(n, ch1, ch2, ch3);

    return 0;
}

image

4）走迷宫：
把地图变成小格去试。用栈的知识。

递归的应用

1）树、森林
2）树、森林、图的很多算法
3）很多数学公式，如斐波那契数列

函数的调用

当在一个函数的运行期间调用另一个函数时，在运行被调函数之前，系统需要完成三件事：

  1. 将所有的实际参数、返回地址等信息传递给被调函数保存。
  2. 为被调函数的局部变量（也包括行参）分配存储空间。
  3. 将控制转移到被调函数的入口。

从被调函数返回函数之前，系统也要完成三件事：

  1. 保存被调函数的返回结果。
  2. 释放被调函数所占的存储空间。
  3. 依照被调函数保存的返回地址将控制转移到调用函数。

当有多个函数相互调用时，按照“后调用先返回”的原则，上述函数之间信息传递和控制转移必须借助“栈”来实现，即系统将整个程序运行时所需的数据空间安排在一个栈中，每当调用一个函数时，就在栈顶分配一个存储区，进行压栈操作，每当一个函数退出时，就释放它的存储区，就做出栈操作，当前运行的函数永远都在栈顶位置。

A函数调用A函数和A函数调用B函数在计算机看来是没有任何区别的。

非线性结构

树

树的定义

专业定义：
1）有且只有一个称为根的节点
2）有若干个互不相交的子树，这些子树本身也是一颗树

通俗定义：（葡萄...）
1）树是由节点和边（指针）组成
2）每个节点只有一个父节点但可以有多个子节点
3）但有一个节点例外（最上面那个），该节点没有父节点，此节点称为根节点

专业术语：
1）节点，父节点，子节点
2）子孙（下面的都是），堂兄弟
3）深度：从根节点到最底层节点的层数称之为深度，根节点算第一层
4）叶子节点：没有子节点的节点（最下面的节点）
5）非终端节点：实际就是非叶子节点
注：根节点可以是叶子节点也可以是非叶子节点，根节点和叶子节点是不一样的判断标准。
6）度：子节点的个数，有几个孩子就是几度。整个树的度是子节点中最大的度

树的分类

1）一般树：任意一个节点的子节点的个数都不受限制

2）二叉树：任意一个节点的子节点个数最多两个，且子节点的位置不可更改
①一般二叉树
②满二叉树：在不增加树层数的前提下，无法再多添加一个节点的二叉树就是满二叉树（除了最下面一层，所有节点的子节点个数都是2，没有子节点个数为1的）
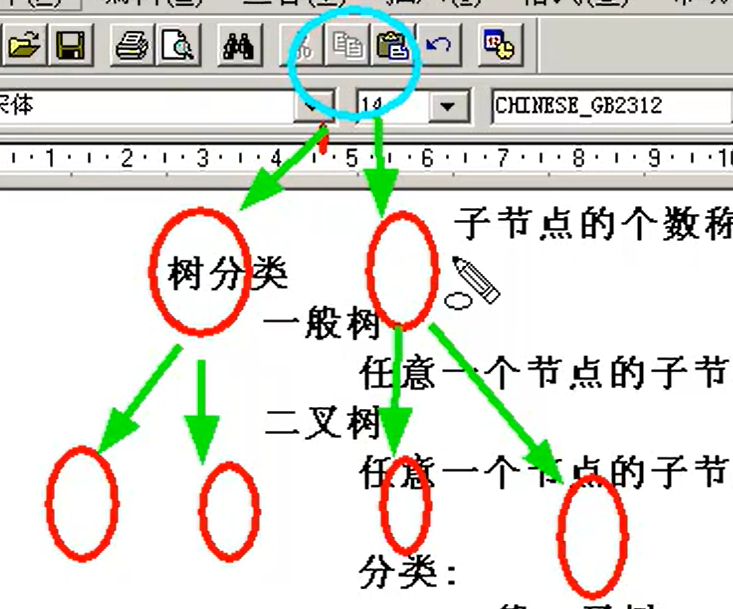
image
③完全二叉树：如果只是删除了满二叉树最底层最右边的连续若干个节点，这样形成的二叉树就是完全二叉树。（满二叉树是完全二叉树的一个特例，即满二叉树一定是完全二叉树，反之不成立）
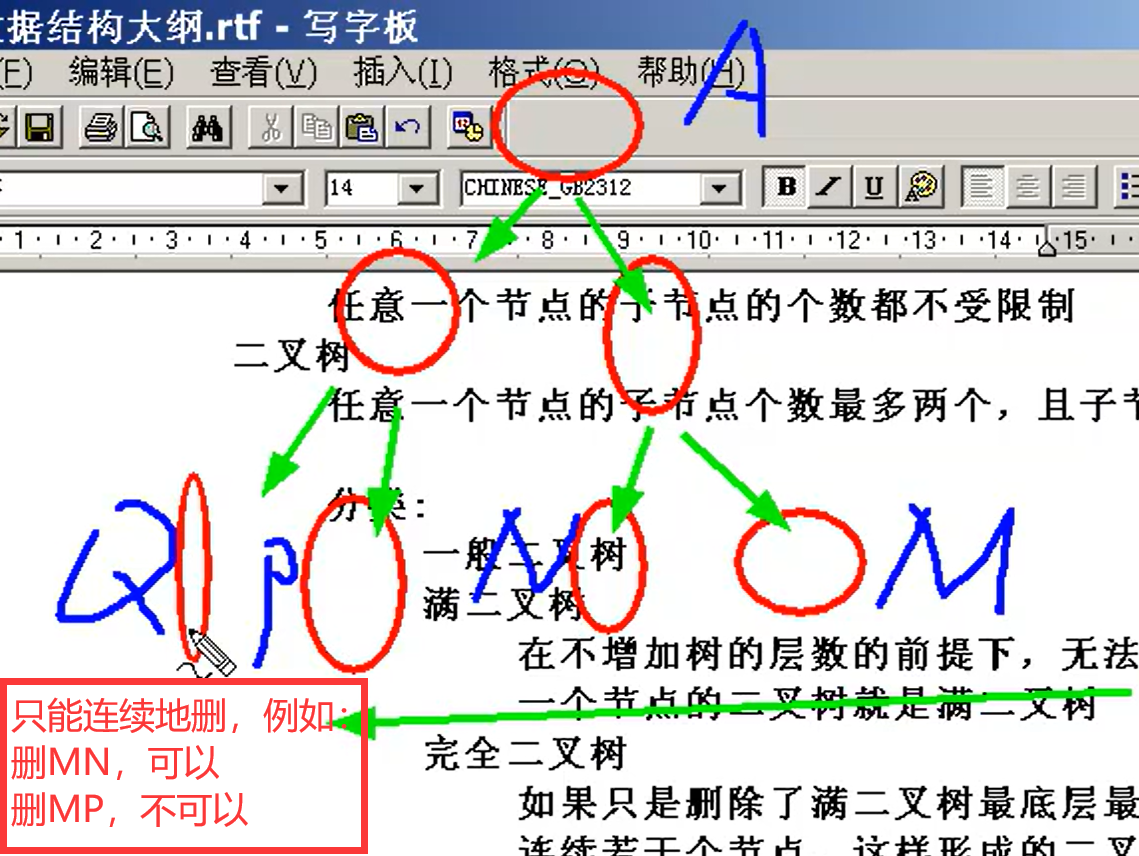
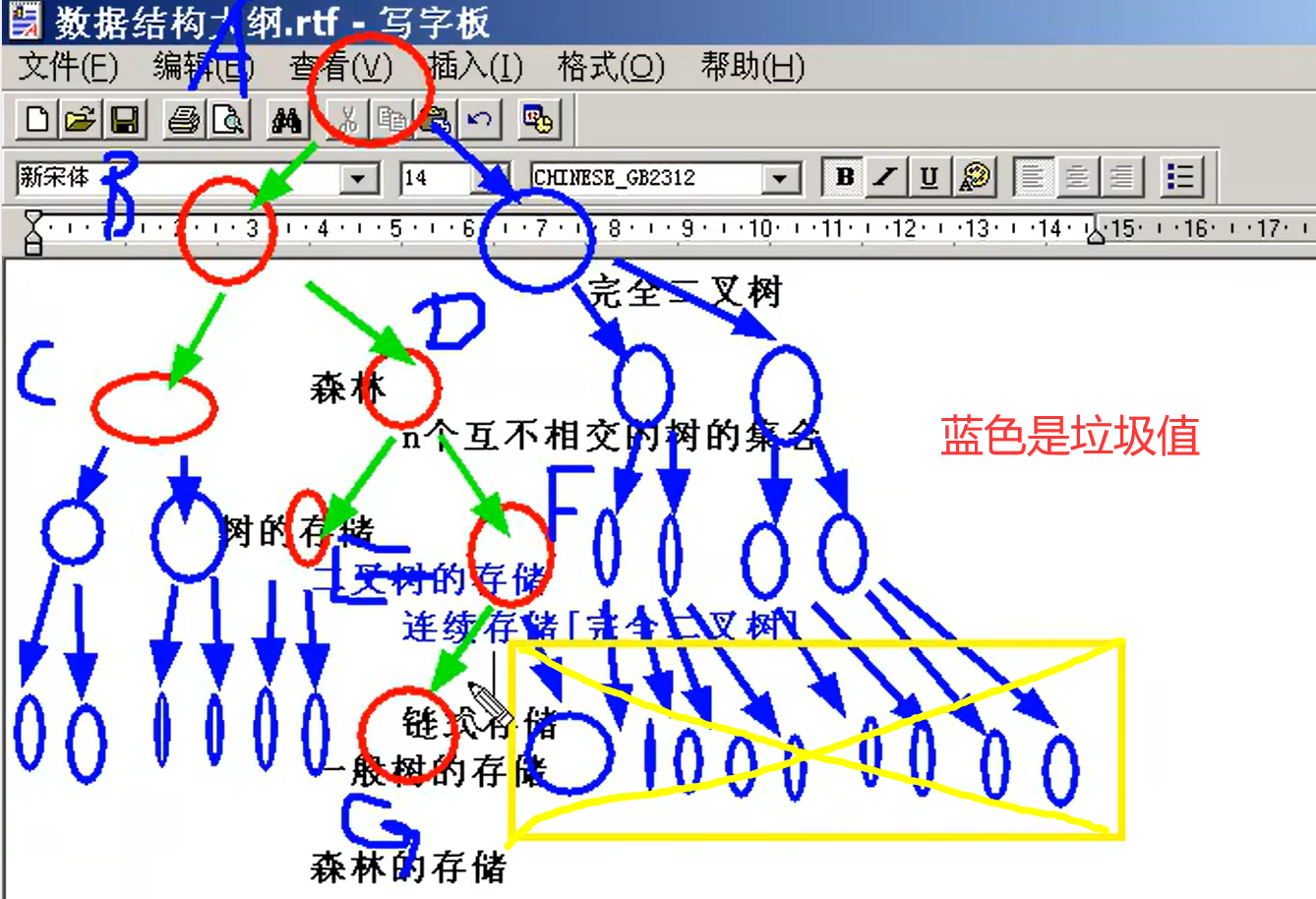
image

3）森林：n个互不相交的树的集合

树的存储

连续存储【完全二叉树】

一般二叉树要转化为完全二叉树才能存
image

优点：

  1. 判断第几层
  2. 查找某个节点的父节点和子节点（也包括判断有没有子节点）速度很快，时间复杂度是0

（完全二叉树，每一行的节点都是固定的数量，我们就能找到使用线性存储的非线性数据）

缺点：
耗用内存空间过大

链式存储

数据域：一块，数据本身
指针域：两块，左孩子，右孩子
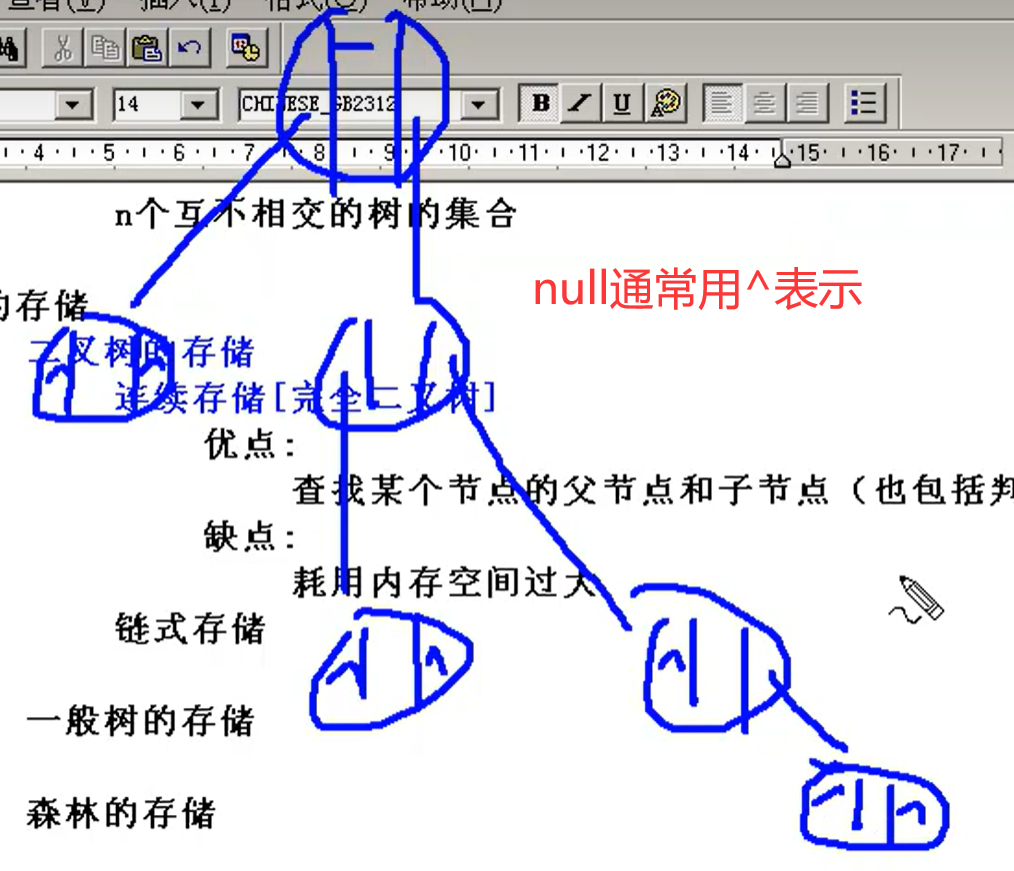
image

一般树的存储

1）双亲表示法：每个节点，保存其父节点的下标。无法确定同一个父节点下子节点的前后顺序（二叉树才行）
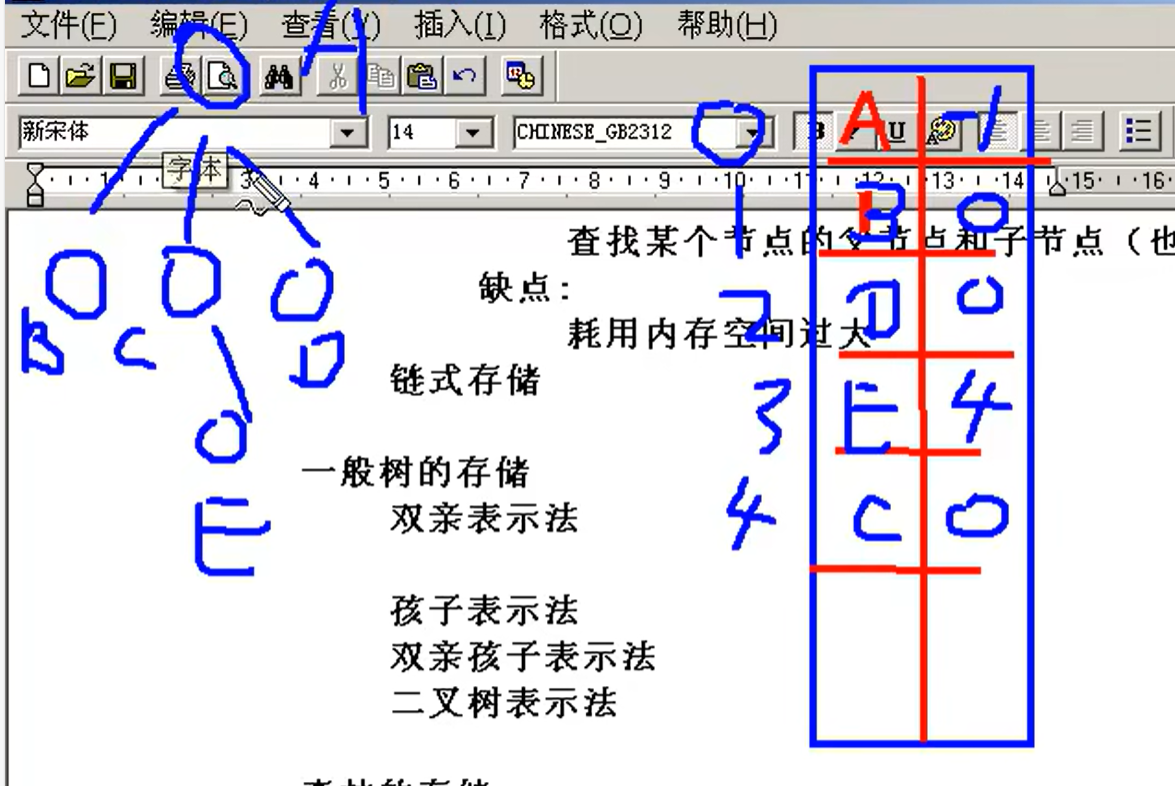
image

2）孩子表示法：每个节点，保存其子节点的一个链表
image
（一般树的存储都是随机的）

3）双亲孩子表示法：结合上面两种方法
image

4）二叉树表示法：把一个普通树转化成二叉树来存储： 每个节点有两个指针，左指针指向其第一个子节点，右指针只向其第一个兄弟节点。
具体转换方法：
设法保证任意一个节点的左指针域指向它的第一个孩子，右指针域指向它的兄弟，只要满足此条件，就可以把一个普通树转化为二叉树。
7

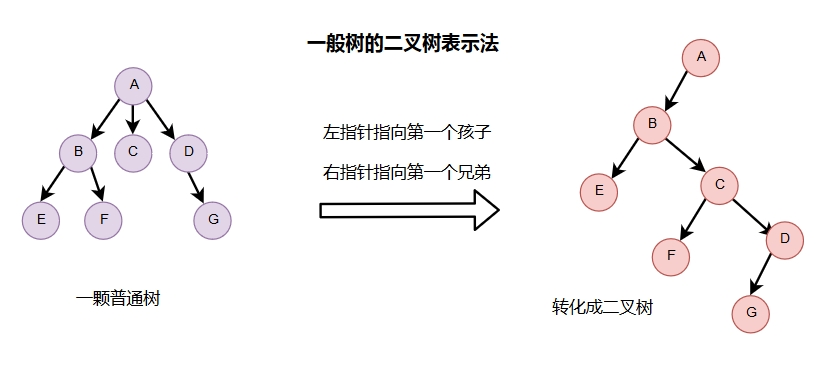
一个普通树转化成的二叉树一定没有右子树（A右下没有子节点）

森林的存储

先把森林转化为二叉树，再存储二叉树：
转化方法跟普通树转二叉树的方式类似（见上点中二叉树表示法的具体转换方法），区别是，森林中， 把多棵树的根节点视作兄弟关系。
将相邻的父节点依次作为节点的右子树再对各父节点进行转化
image

二叉树操作

遍历

都是递归的

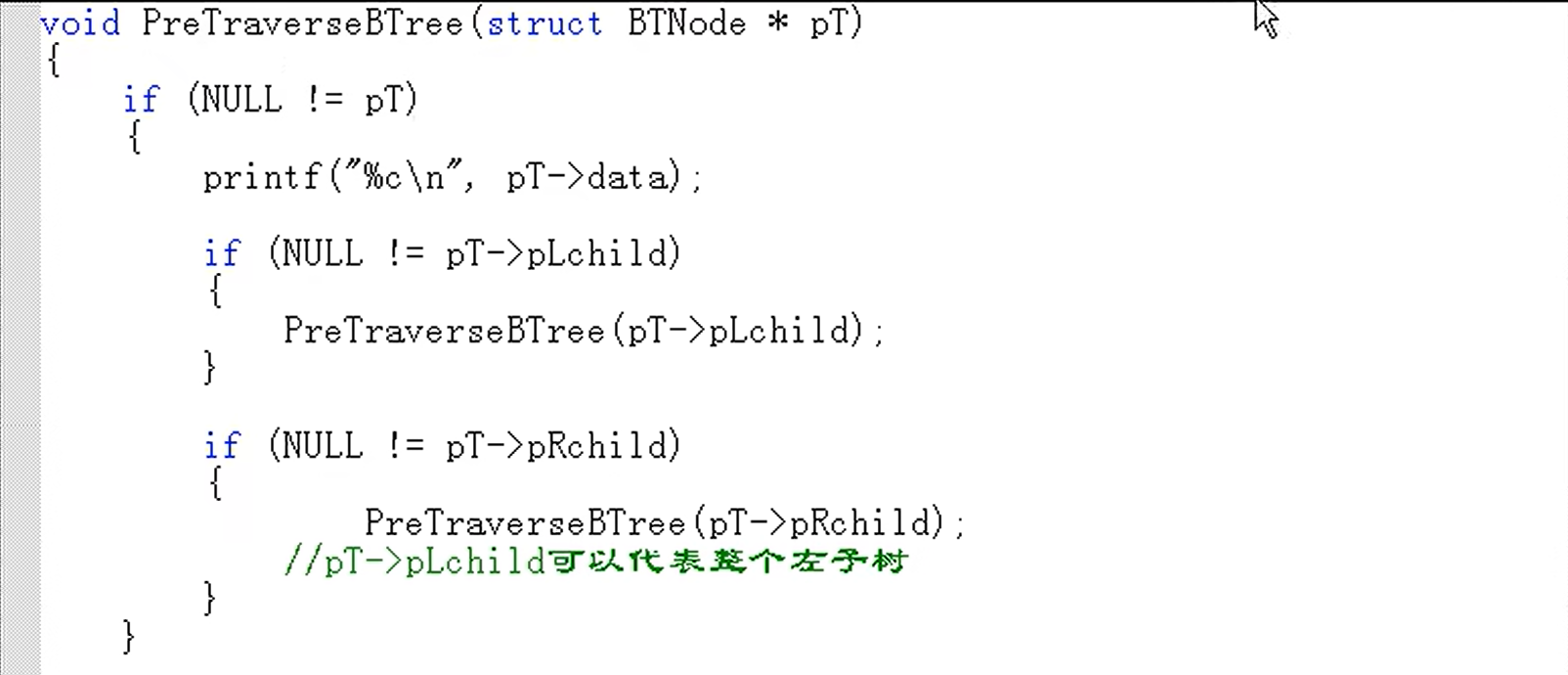
先序遍历【先访问根节点】

先访问根节点
再先序访问左子树
最后先序访问右子树
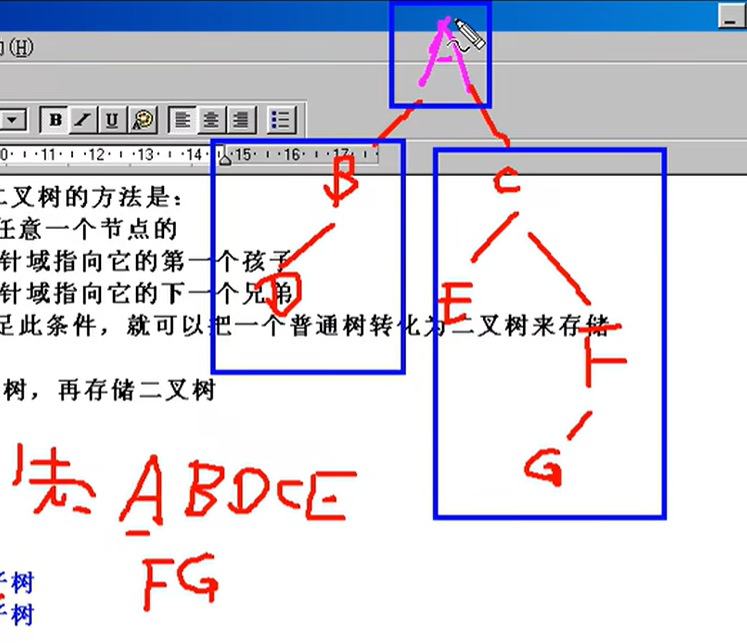
image

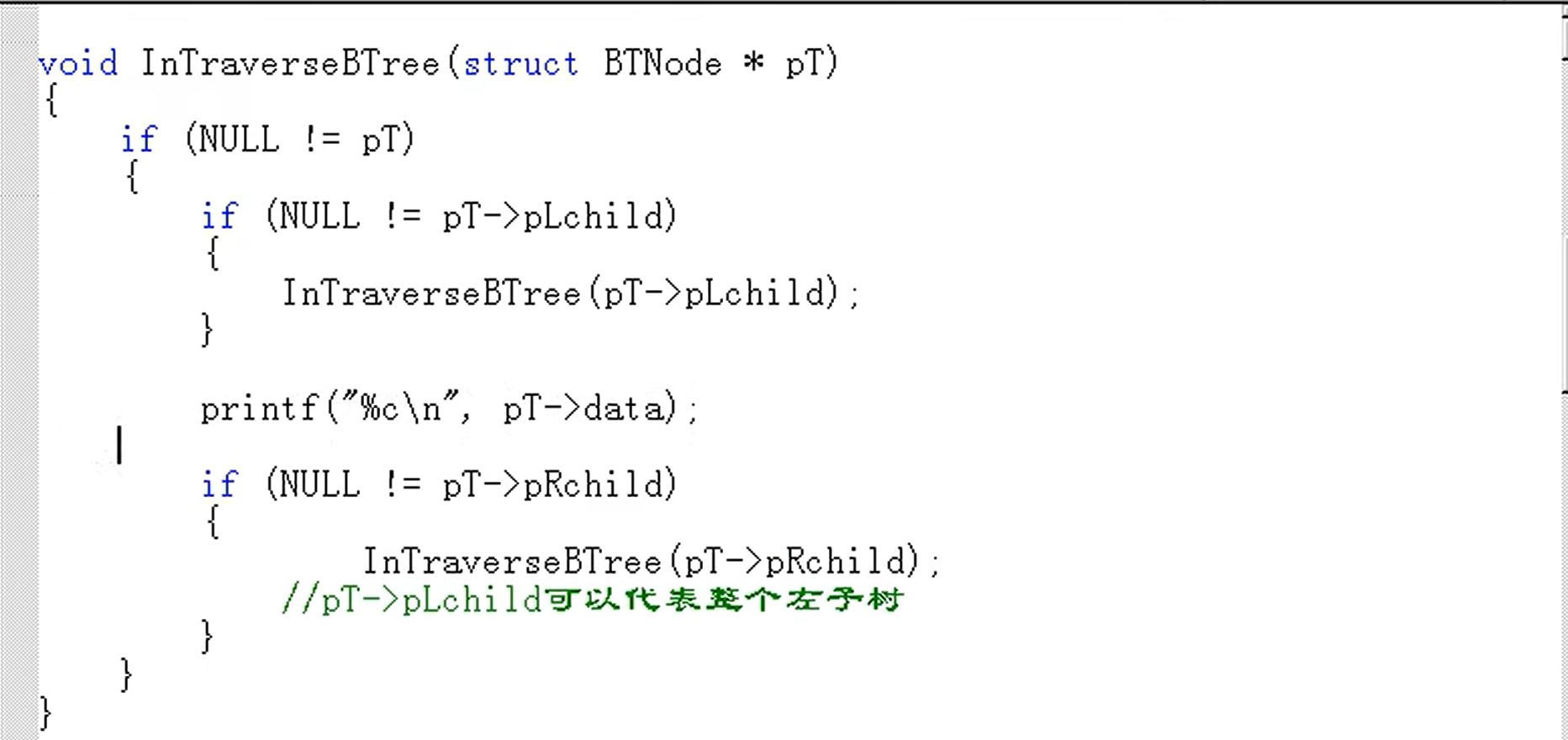
中序遍历【中间访问根节点】

中序遍历左子树
再访问根节点
再中序遍历右子树
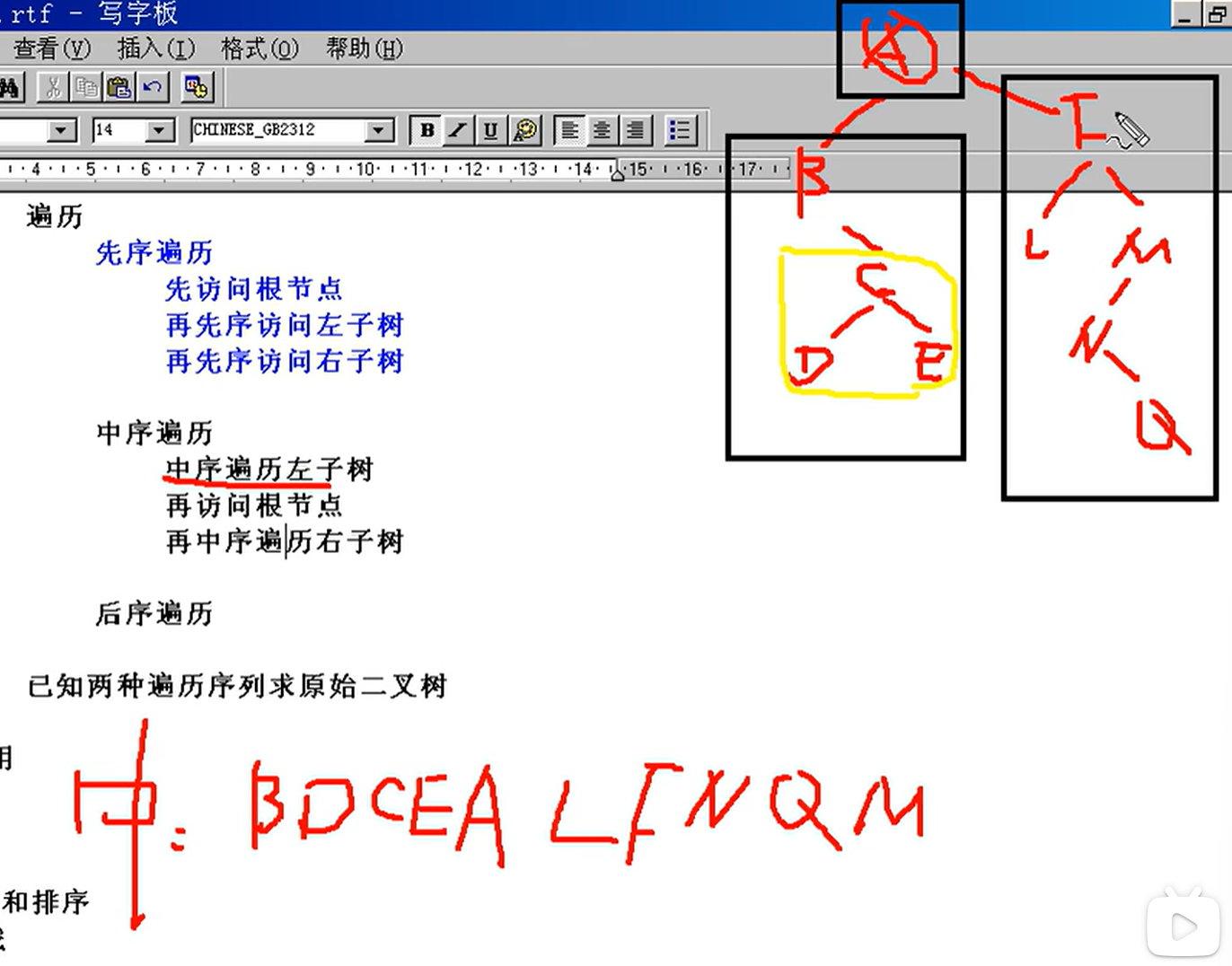
image

后续遍历【最后访问根节点】

先中序遍历左子树
再中序遍历右子树
最后遍历根节点
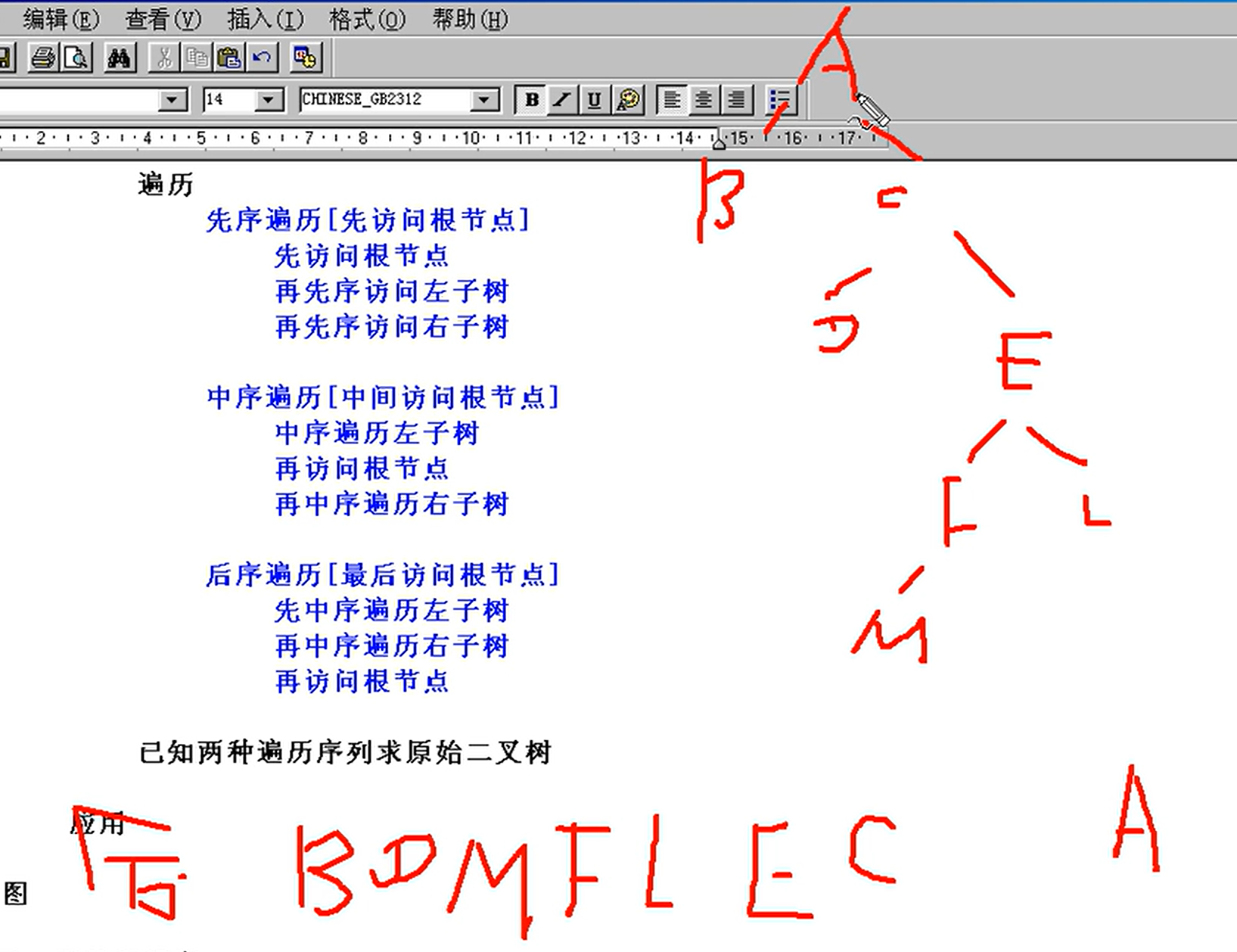
image

已知两种遍历序列求原始二叉树

已知一个遍历序列，无法推出原始二叉树的样子。 但是，已知先序和中序，或者已知中序和后序，可以推出。 （但是，已知先序和后序，也是无法推出的。也就是说要 中序 + 另一种）

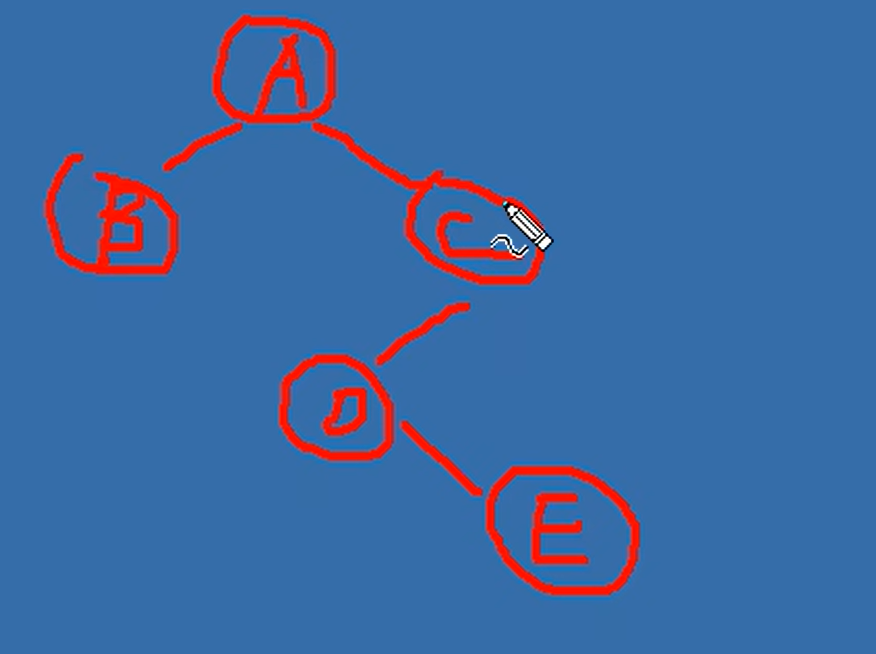
先序 + 中序 推理方法：
（画图！）

  1. 先序第一个是根节点
  2. 中序中根节点左边是左子树，右边是右子树
  3. 左右子树中，继续看先序，先序中先出现的必定是左子树的根
  4. 重复步骤1~3

例子：
先序：ABCDEFGH 中序：BDCEAFHG
--> 后序：DECBHGFA
先序：ABDGHCEFI 中序：GDHBAECIF
--> 后序：GHDBEIFCA

后序 + 中序 推理方法：

  1. 后序最后一个是根节点
  2. 中序中根节点左边是左子树，右边是右子树
  3. 左右子树中，继续看后序，后序中最后出现的必定是右子树的根
  4. 重复步骤1~3

例子：
中序：BDCEAFHG 后序：DECBHGFA
--> 后序：ABCDEFGH

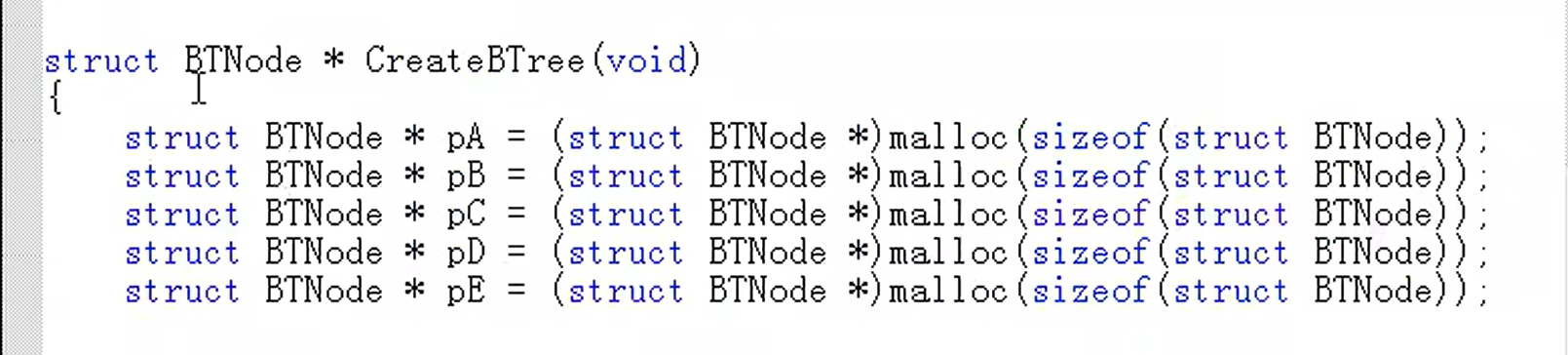
链式二叉树遍历代码

（静态）
MGLU

KY2GP23GO
HGOHX${2ZV$6JEJ%R01ZX0I
N_C
WX$ZCOJNS}K4)ZUS9ZCDTKE
Y48
DR
2FWKF
)ZGZEEEB4YA32WD%1Y0EOO7
YE6

树的应用

1）树是数据库中数据组织的一种重要形式。例如文件系统。
2）操作系统子父进程的关系本身就是一颗树。
3）面向对象编程中的类的继承关系就是树。
4）霍夫曼树

图

查找和排序

排序是查找的前提，排序是重点。

查找

  • 折半查找

排序

  • 冒泡排序：
    先让N个元素从左到右两两比大小，大的放后面，从而让最大的排到队尾； 再让前N-1个这样做，让第二大的排到队尾前一个； 以此类推。
  • 插入排序：
    把第二个插入到前一个，使前两个有序； 把第三个插入到前两个，使前三个有序； 以此类推。
  • 选择排序：
    先从所有N个数中，选最小的，跟第一个位置互换； 再从剩下的N-1个中，选最小的，跟第二个位置互换； 以此类推；
  • 快速排序：
    每次确定第一个数的排序后的位置，把列表一分为二，大的在右边，小的在左边； 然后将两边的数列进行上面同样的操作。
  • 归并排序：
    两两比较，并排序； 再在上一层的基础上，再两两比较，并排序； 以此类推。 （先两两有序，再四个四个有序，再八个八个有序......）

详细内容及代码见：
https://www.runoob.com/cprogramming/c-sort-algorithm.html

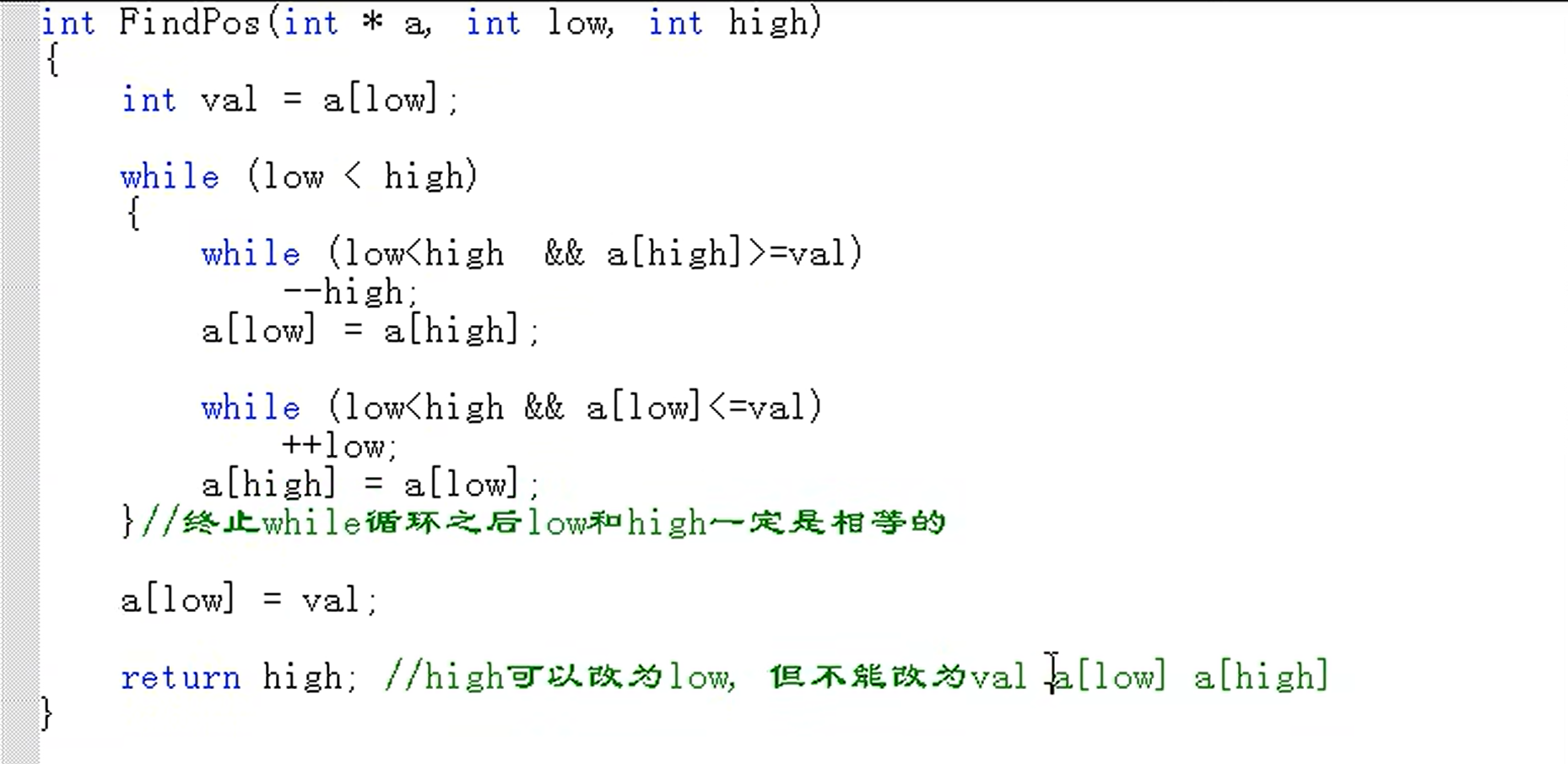
快速排序

先确定第一个元素该排在哪里，分成左边一半和右边一半，然后递归，继续如上操作
步骤：

  1. （需要升序）
  2. val = 第一个元素的值，l 指向最左元素，h 指向最右元素
  3. h 左移，遇到比 val 小（因为升序，右边需要更大）或等的元素，把 h 的值赋给 val，然后 h 不动（注意是先移h！）
  4. l 右移，遇到比 val 大或等的元素，把 l 的值赋给 val，然后 l 不动
  5. 重复操作2~3，h l 重合时停止
  6. h l 重合处就是最终存放第一个元素的位置
  7. 根据以上步骤排序完得到的就是第一次排序的结果
  8. 然后以排序前第一个元素排序后的位置为中心点分成左右两半，分别再对左右两半重复步骤1~6

代码：
2SXD0
_UZVR
@@2UXQV9

参考

笔记参考：
https://www.cnblogs.com/flmei/articles/10768617.html
https://gitee.com/guobiyang/data_structure_learning
视频：
【【递归1】递归中的逆向思维】 https://www.bilibili.com/video/BV1214y157HG/?share_source=copy_web&vd_source=615eb03d223cf19a23232ca4a7b70c1e
其他参考：
https://www.zhihu.com/question/24385418

相关文章：

  1. python3字典
  2. 机器学习笔记
  3. 多媒体安全实验课记录
  4. 隐写术相关笔记

发表评论

备案号： 闽ICP备2023012001号