本学期多媒体安全课程的实验记录,记录一些以前不太了解的操作和理论内容
目录
实验1 图像频域变换与滤波
图像的傅里叶变换
用傅里叶变换将图像从空域转换到频域,并显示频谱图像

1)代码中fft2、fftshift、log函数的作用分别是什么?
fft2:对图像进行二维傅里叶变换,将图像从空间域转换到频率域,输出复数频谱。
fftshift:将二维傅里叶变换的频谱数据零频分量从角落移到中心,便于观察和分析频谱。
log:对频谱数据进行对数变换,增强频谱的低强度部分以便更好地显示细节。
2)频谱(幅度谱)的计算方式是什么?图1代码中的real函数是否应替换为abs函数?为什么?
① 幅度谱的计算公式:
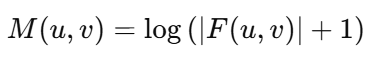
其中,∣F(u,v)∣是复数频谱的模。
② 代码中的 real 是否应替换为 abs:是。
原因:傅里叶变换结果是复数,只有取模(绝对值)才能正确表示频谱的幅度信息,而real 仅提取复数的实部,会导致频谱信息丢失。
3)在正确代码的条件下,实验使用和不使用fftshift、log函数的差异,将结果填入表,并分析差异原因。
输出结果:
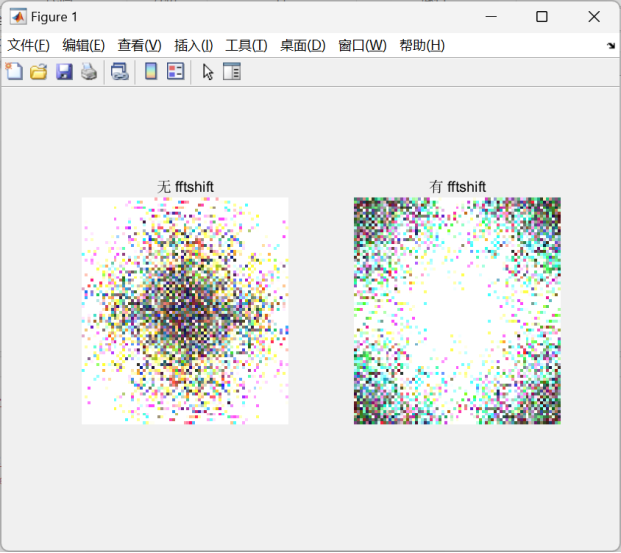
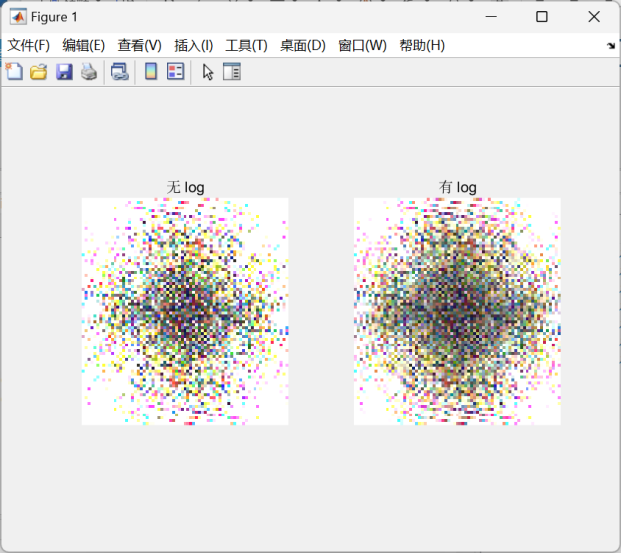
| 有 | 无 | 差异原因 |
|---|---|---|
| fftshiftt函数 | 零频分量在中心, 分布对称 | 零频分量在角落, 分布不对称 |
| log函数 | 低强度细节增强, 动态范围小 | 动态范围大, 低强度部分较暗 |
注:
白色是低频,高强度;黑色高频,低强度
低频平滑;高频快速变化,是细节
扩展:DCT低频系数大,高频系数小常被舍弃(是细节,对图像整体贡献小,人眼察觉度低)
强度 能量:理解为在图像中占据的面积(高能量==>不是“小”细节)
频域滤波器的设计与实现
1)设计一个理想低通滤波器和一个理想高通滤波器。

2)使用这些滤波器对频域图像进行滤波,分别去除高频和低频成分。

3)将滤波后的频域图像转换至空域,观察其与滤波前的空域图像存在哪些差异?
差异如下:
通过对比滤波前后的空域图像,可以发现:低通滤波保留了图像的低频部分(整体轮廓和平滑区域),去除了高频细节,导致图像变得模糊;而高通滤波保留了图像的高频部分(边缘和细节),去除了低频背景,使图像呈现出强烈的轮廓效果。这种差异说明频率成分的不同对图像特征的表达具有显著影响,低通适用于去噪或平滑处理,高通则适用于边缘提取或增强细节。
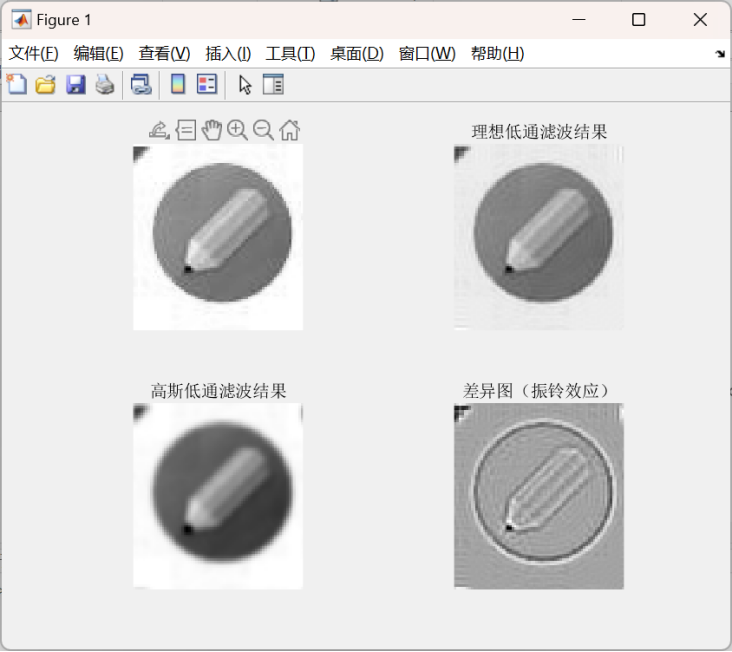
4)观察理想滤波后的图像是否存在振铃效应?说明如何去除振铃效应并进行实验验证。
答:存在振铃效应。
去除振铃效应方法:
1)使用平滑的频域滤波器:例如高斯滤波器或巴特沃斯滤波器,它们在频域中边界光滑过渡,避免了频率的突变。
2)调整滤波器的截止频率:适当提高或降低截止频率,避免过强的截断。
3)窗函数处理:对滤波器应用窗函数(如汉宁窗、海明窗)以减缓频域的不连续性。
实验2 图像隐写
1.选择一幅隐写载体图像,生成载体图像8个位平面所对应的二值图像,并对其差异进行解释。
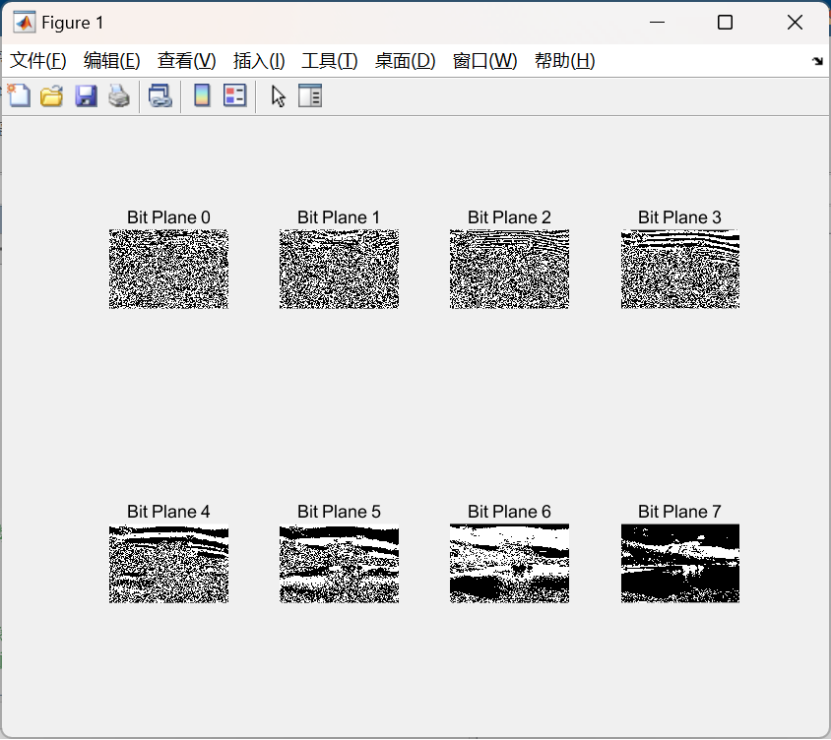
位平面分解将灰度图像的像素值按二进制表示分解为8个位平面,从最低有效位 (Bit Plane 0) 到最高有效位 (Bit Plane 7)。每个位平面展示了图像不同层次的信息,低位平面通常包含较多随机性,而高位平面包含图像的主要特征。
低位平面 (Bit Plane 0 到 3) 噪声较多,随机性强,难以分辨图像结构,说明它们承载的图像信息较少。中位平面 (Bit Plane 4 和 5) 开始显现图像的边缘与结构,随机性逐渐降低。高位平面 (Bit Plane 6 和 7) 则清晰地展现了图像的主要内容和细节,尤其是 Bit Plane 7,几乎完全保留了原始图像的显著特征。
这反映出图像的大部分视觉信息集中在高位平面,而低位平面主要反映噪声和细微变化。通过这种分解,可以理解图像中各个位对信息的贡献,并为图像压缩或加密提供参考,例如优先保留高位平面以保留图像的主要特征。这种方法广泛用于图像处理与分析领域。
实验3 JPEG压缩特性取证
实验原理:
1)JPEG图像在压缩时,会将图像分为8×8的块并进行离散余弦变换(DCT),随后进行量化和编码。
2)篡改JPEG图像后,篡改区域与背景的JPEG块结构可能不对齐。这种对齐偏移会在重压缩后显现为不同的压缩特性。
3)偏移后每个像素的信息损失被记录为偏移均值图(Shifted Average Map, SAM)。通过分析SAM中的峰值位置,可以判断篡改区域。
算法流程:
1)图像分块:将输入图像分为非重叠的8×8块,按不同的偏移量移动子块。
2)计算信息损失量:对每个偏移量,计算压缩前后的信息损失。
3)生成SAM图:记录每个偏移位置的信息损失,形成SAM图。
4)篡改区域检测:比较篡改区域与背景的压缩特性,定位篡改区域。
实验4 基于Benford's Law的JPEG双压缩取证
Benford's Law 是一种统计现象,描述了自然界中数字的首位分布规律。根据该定律,数字 1 作为首位数字的概率最大,随后依次递减,数字 9 作为首位数字的概率最小。其概率公式为:
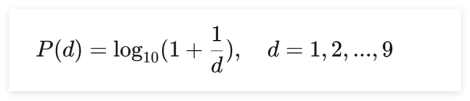
在 JPEG 双压缩图像取证中:
- JPEG 双压缩:是指图像经过两次 JPEG 编码,这可能由于图像的修改、重新保存或其他操作导致。
- Benford's Law 应用:JPEG 图像的离散余弦变换 (DCT) 系数,其统计分布与 Benford's Law 有一定的符合度。未压缩或单次压缩图像的 DCT 系数更符合 Benford's Law,而双次压缩图像由于量化误差的累积,会偏离这一规律。
- 取证原理:通过比较 JPEG 图像 DCT 系数的首位分布与 Benford's Law 的理论分布,可以判断图像是否可能经过了双次压缩。