第1,3~4章使用课程来自b站:复旦发哥带学408
第6~7章使用王道课程
第2,5章二者皆有
也有许多知识点来自b姐的视频
目录
第1章 计算机系统概述
计算机层次结构
计算机硬件
冯诺伊曼基本思想
计算机功能部件
MAR和MDR
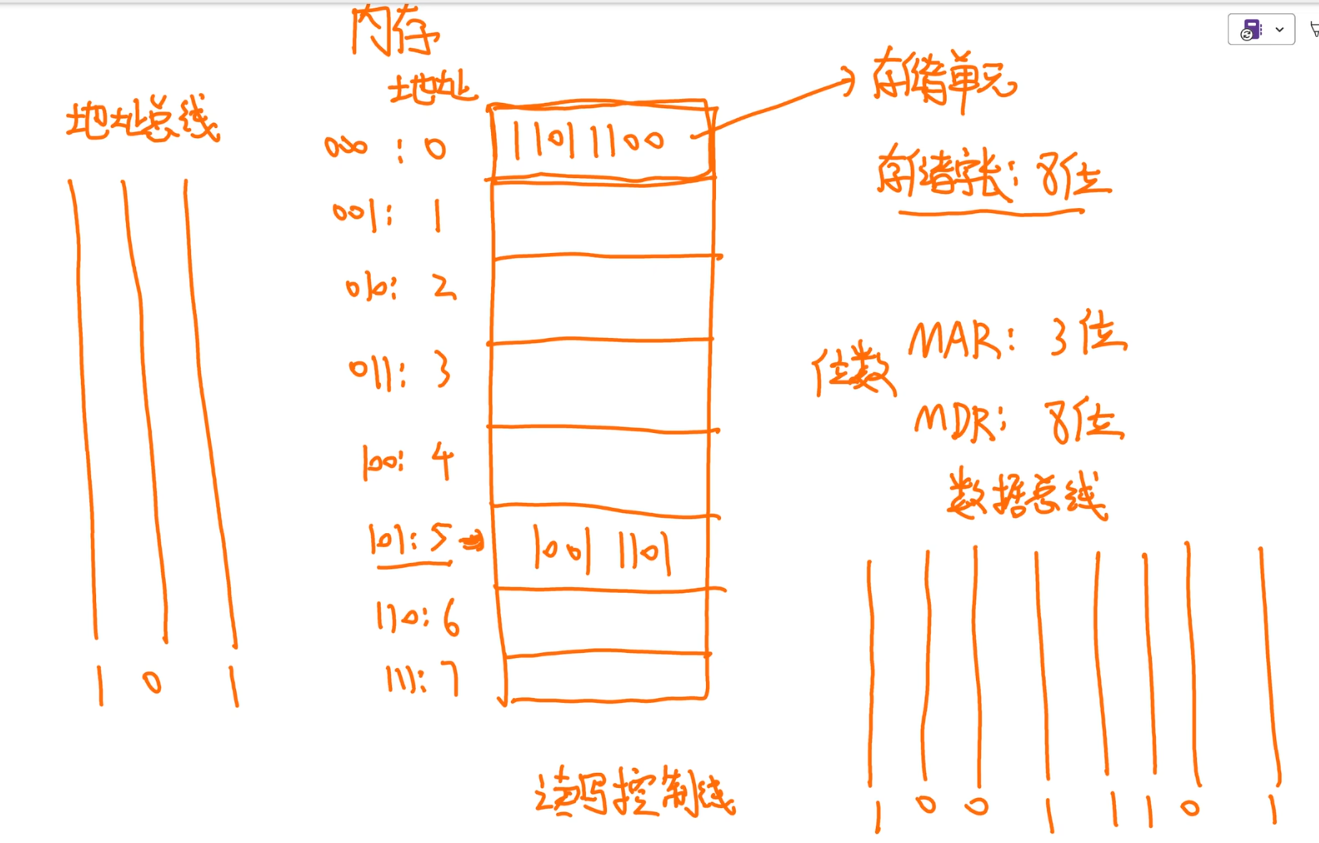
内存容量:8*8
$2^{MAR}×MDR$
例:p13 3.
“n位的计算机”means:计算字长n位,即一次可以处理n位的数据
“以m位来表示地址”means:地址码的长度,即MAR的位数
=> 地址空间:$2^m$
这里有很多的概念,看书p3-4
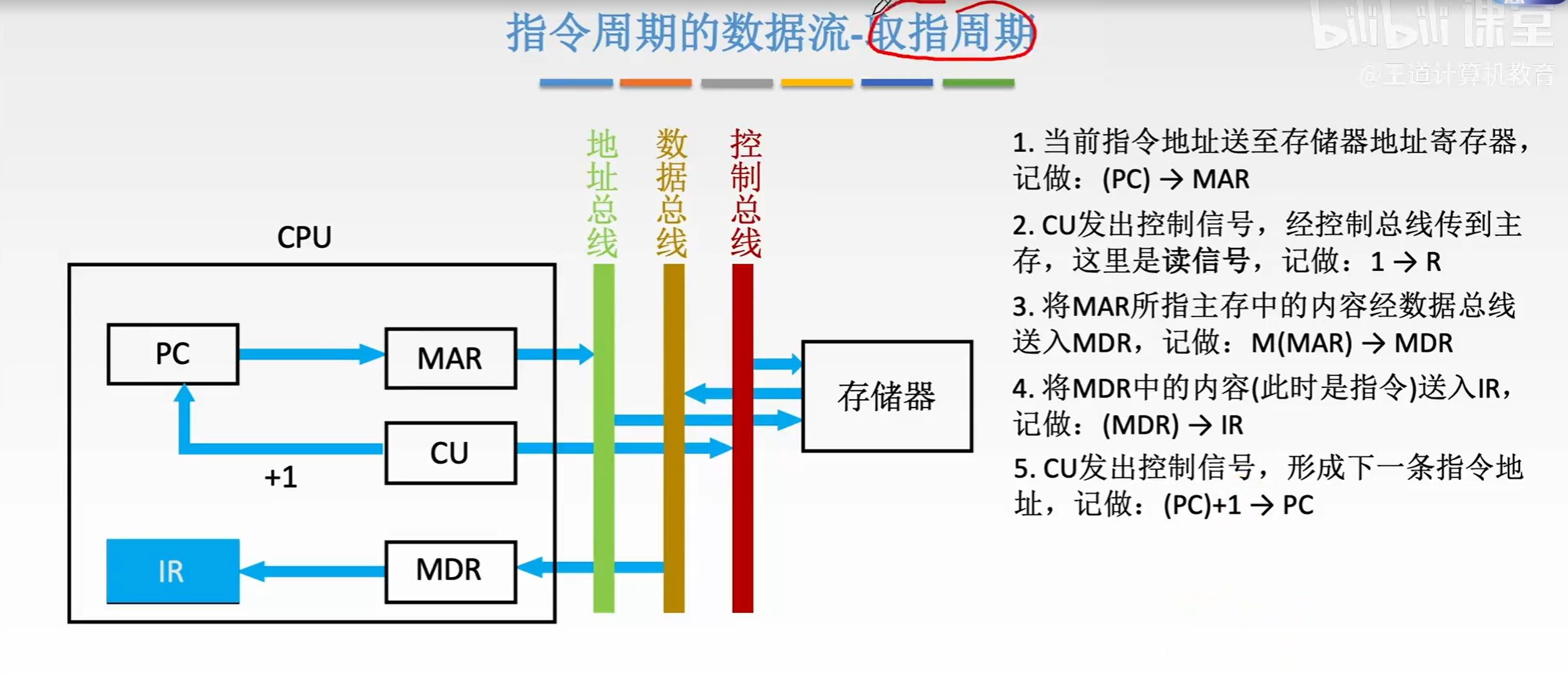
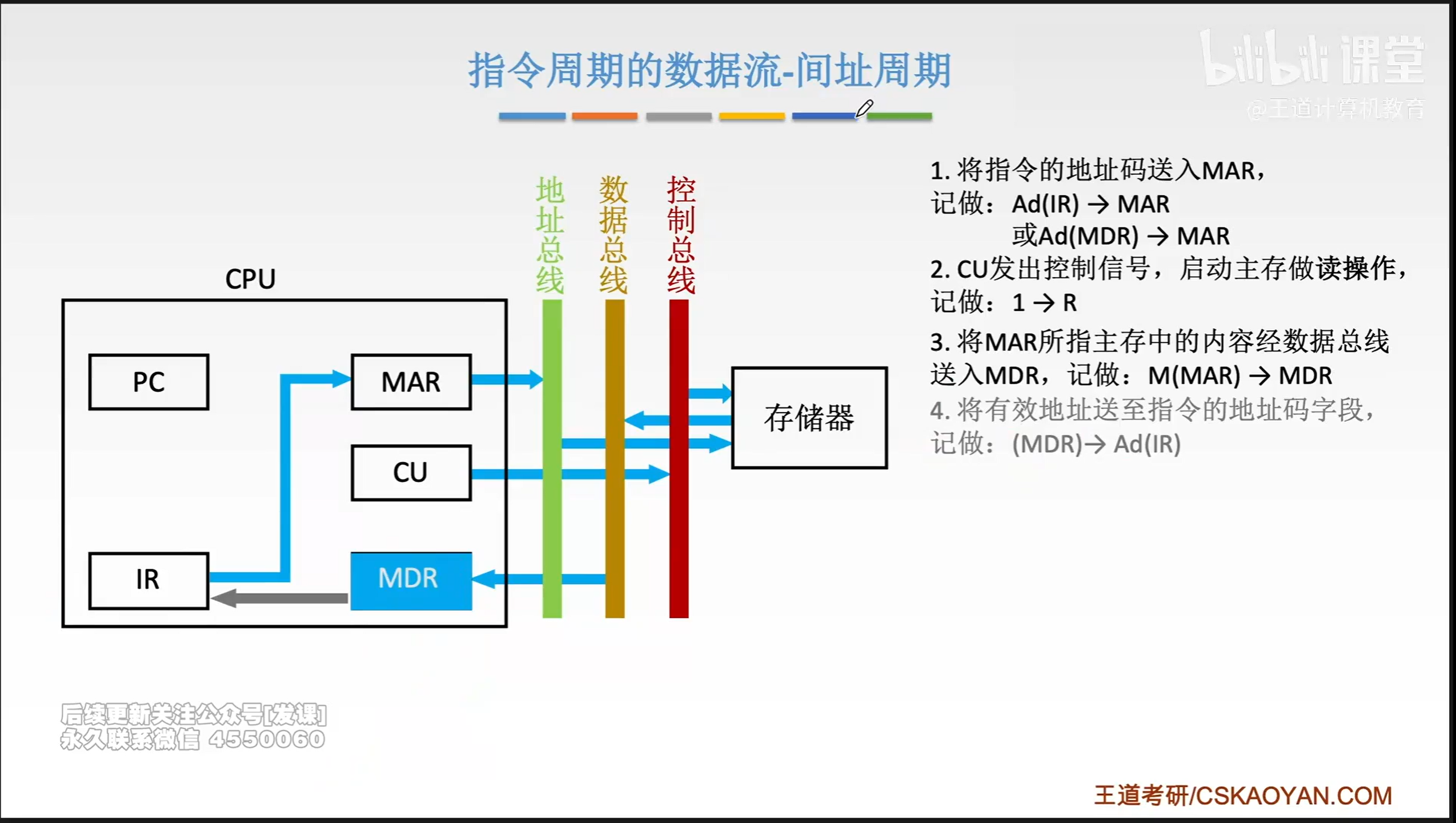
PC->MAR->地址总线->定位到具体地址->数据总线(指令)->MDR->IR(OP)->CU
...IR(Ad)->MAR(看图片)
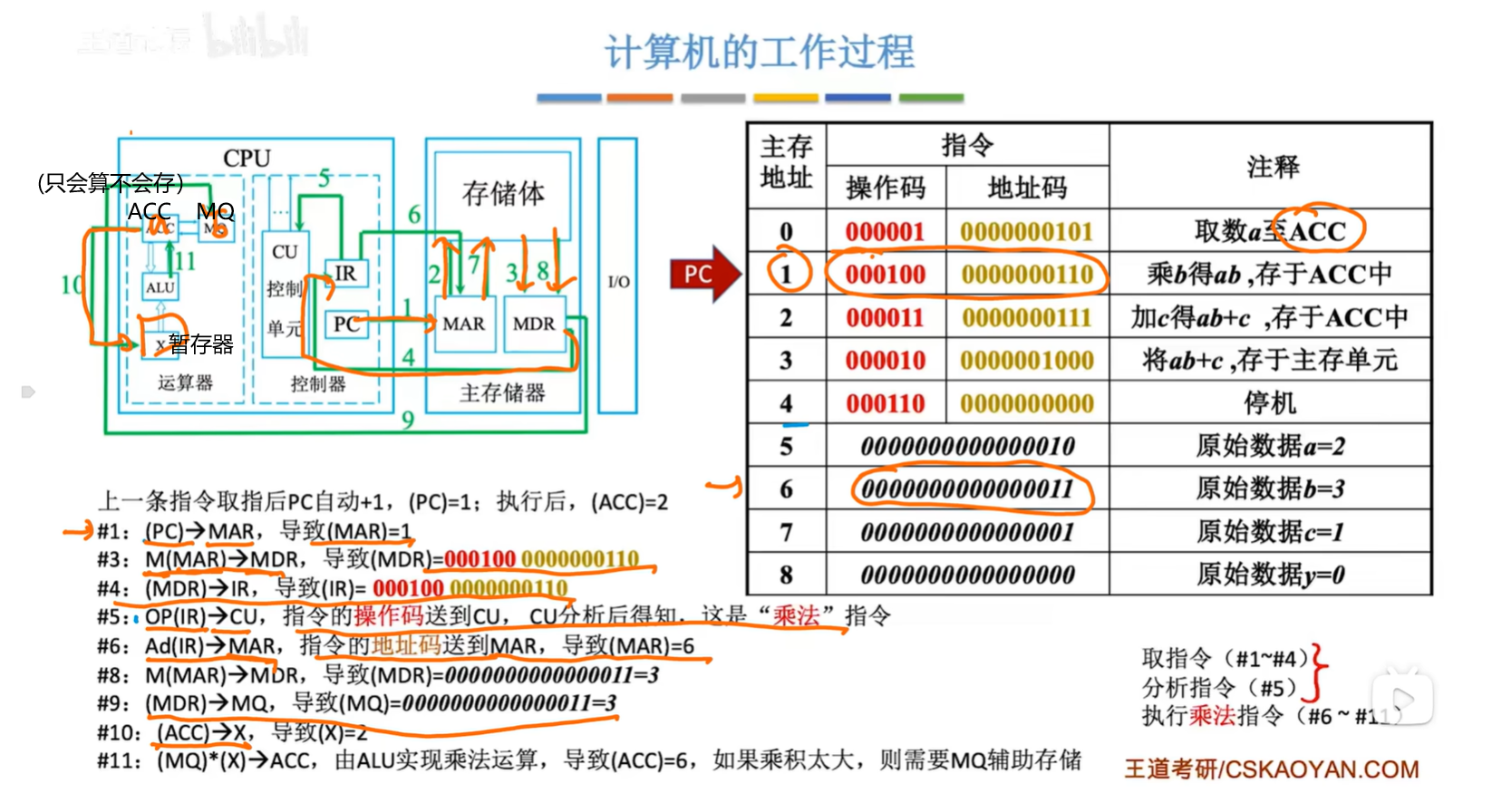
#3取指令,#8取数据
计算机性能指标
计算机主要指标
书p12-p14:
概念
CPU执行时间的计算(两个公式)
第2章 数据的表示与运算
数值与编码
进制转换
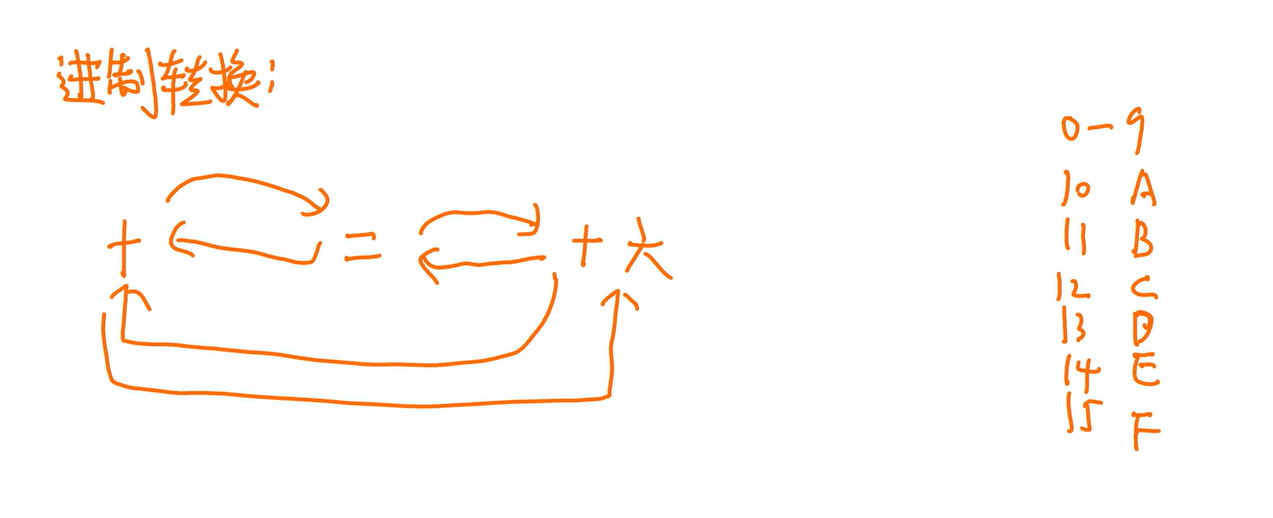
2转10
类比十进制书写
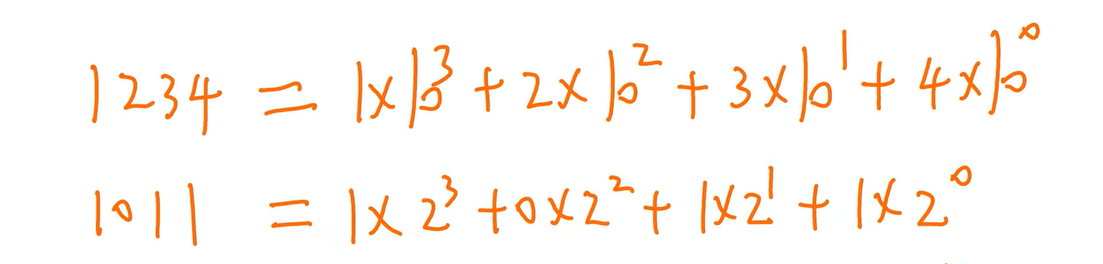
10转2
麻烦的做法:短除法
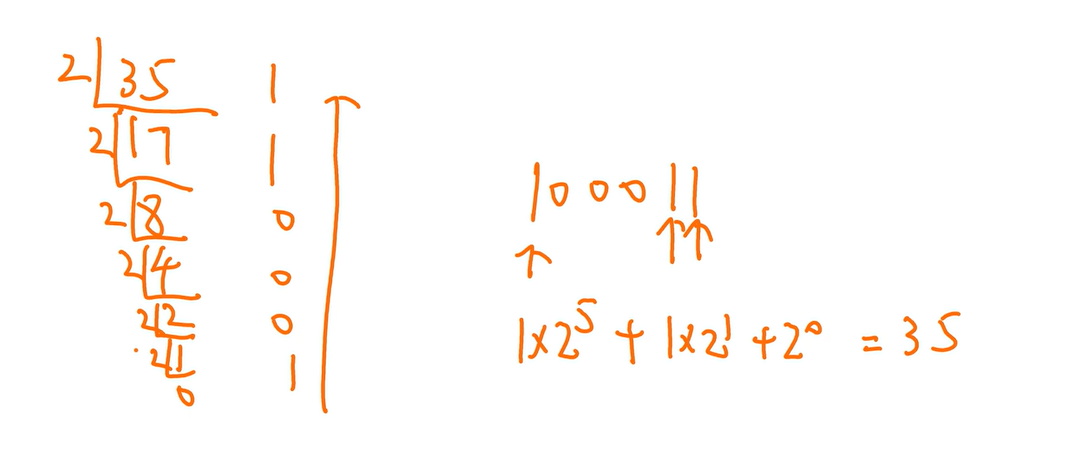
快一些的做法(用这个):拼凑
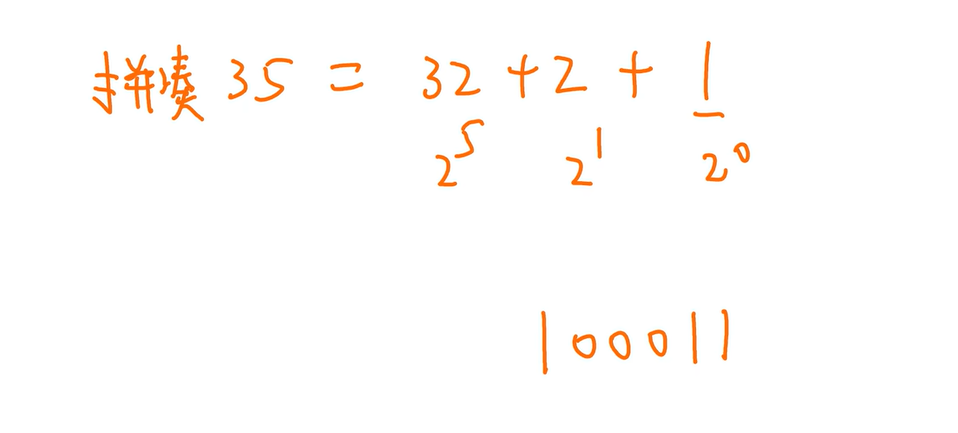
2转16 与 16转2
从后往前,4个一组,不够就补0
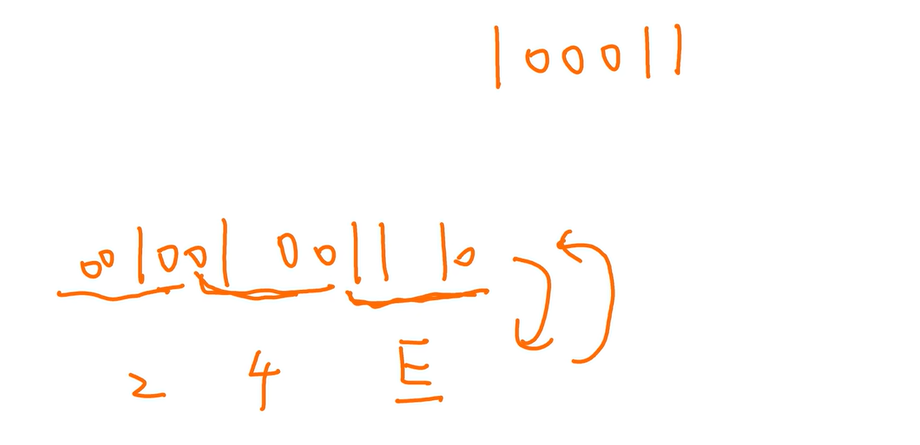
10转16
类比计算十进制每位的数值
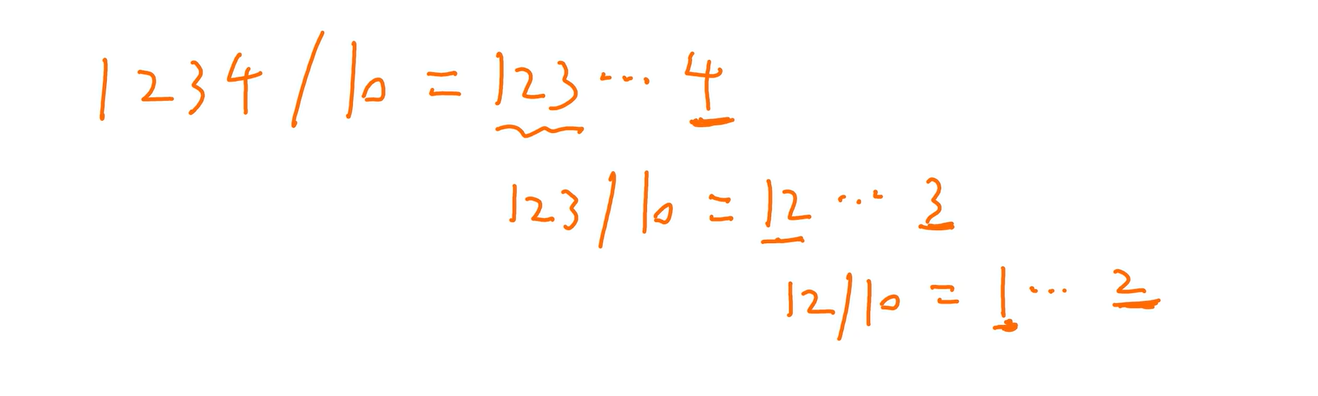
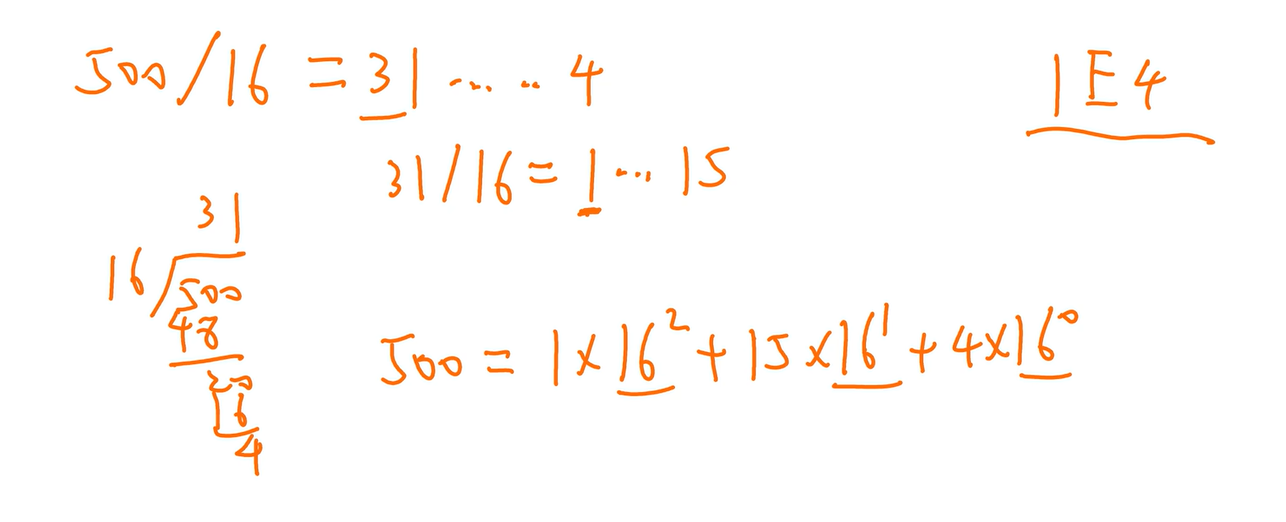
得出的余数从后往前排,某一次商在16以内就停下(比如这里是1)
也可以拼凑法,但不太好拼(上图中下面使用的方法)
先转成二进制再转到十六进制也行
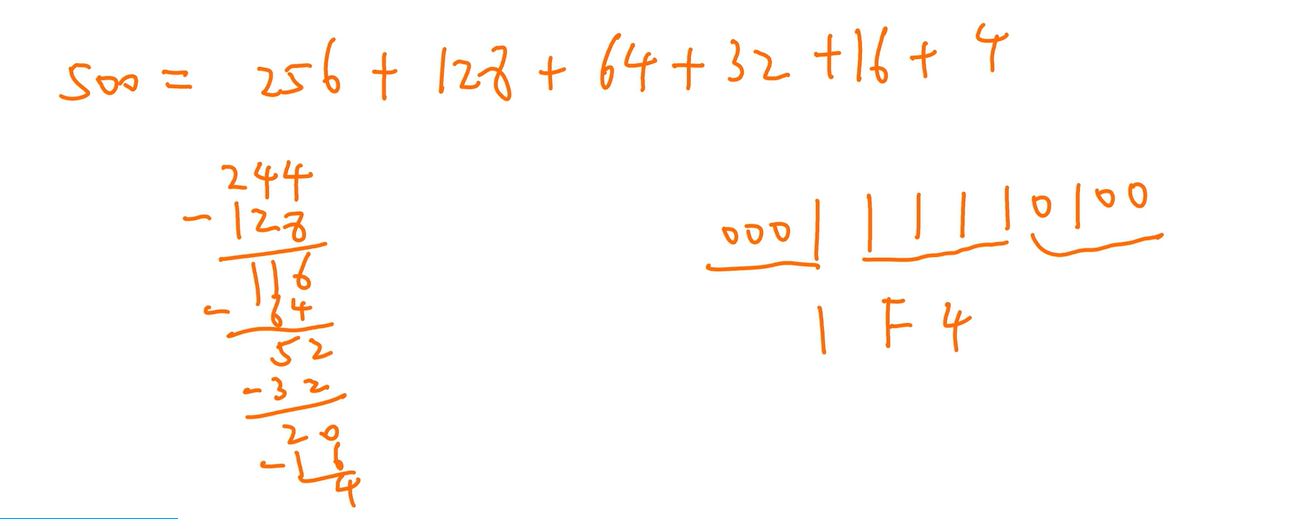
常见二进制
1)1后面有几个0,就是2的几次方
2)有几个1,就是2的几次方-1
类比二叉树的结点计算
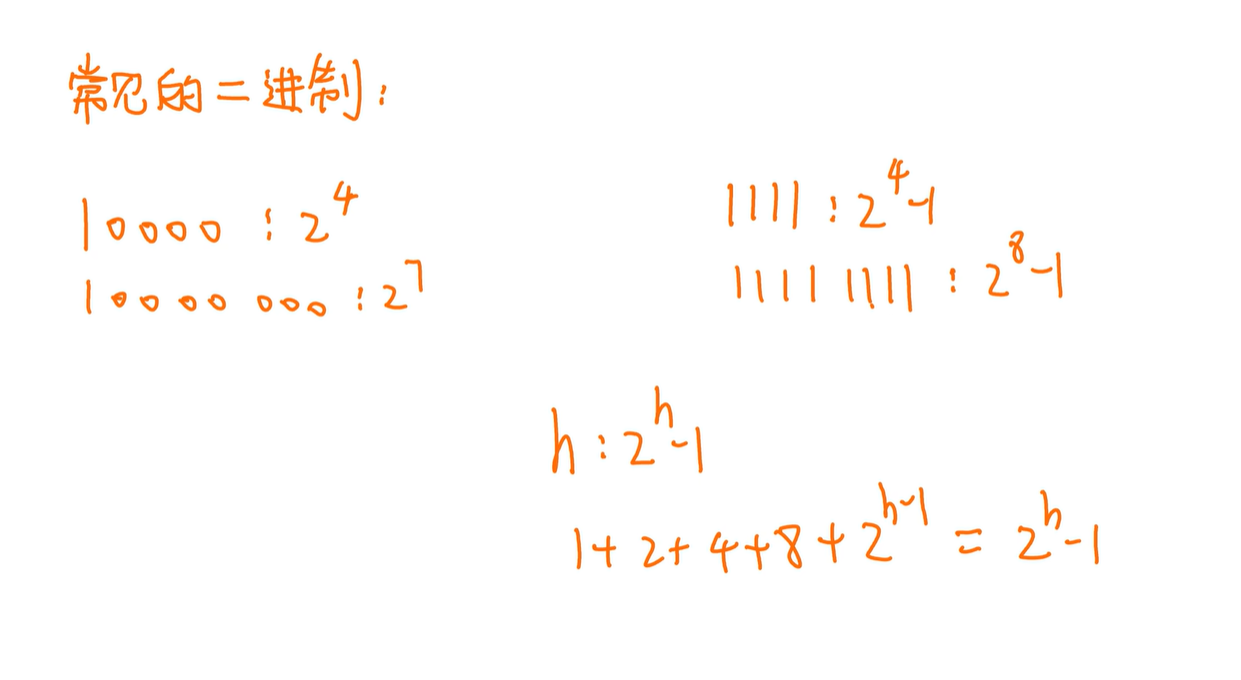
$2^{15} = 32768$
$2^{16} = 65536$
16个1就是 65536-1=65535
定点数的编码表示
定点整数和定点小数
定点小数:小数点在前,每位2^(-n)
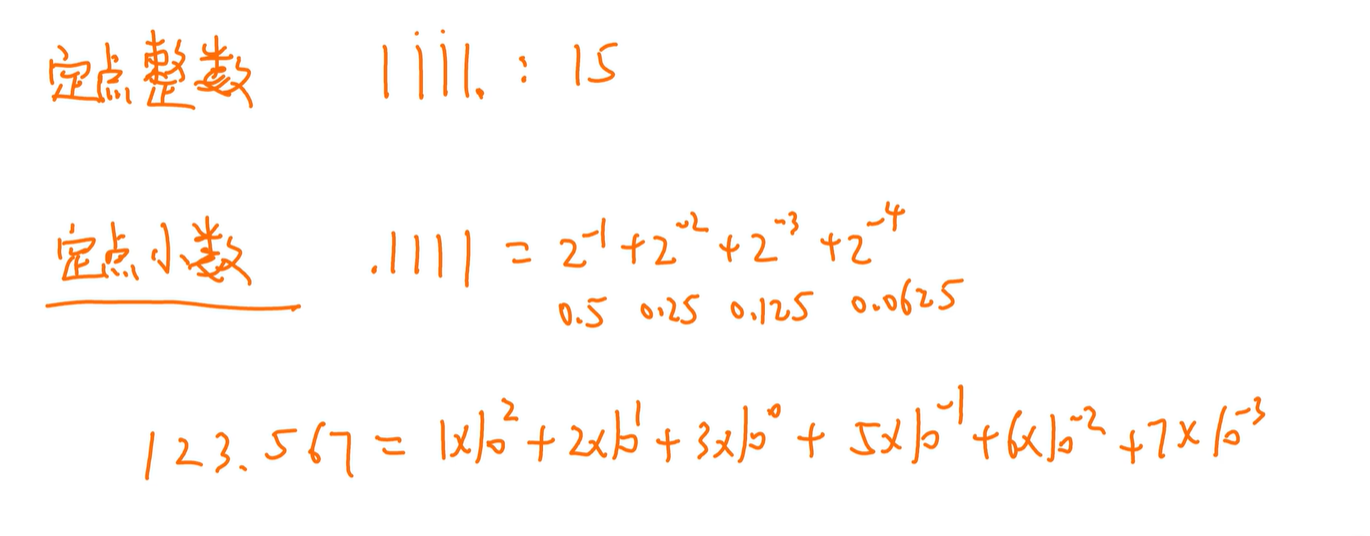
(记一下前面几位的数值)
小数点不会存进去,题目没说默认是整数
机器数和真值

补码和原码
转换
算补码
正数补码=原码
负数:符号位不动, 按位取反,末位+1(算得很慢)
(用这种方法快:)符号位不动,从右往左数到第一个1,右边0不变,符号位和右边第一个1中间的位数全部取反

补码转原码,原码转补码操作一样
补码的性质
补充:
0的补码是唯一的
(以8bit为例)
0的原码是0000 0000(即正零)
1000 0000(负零)是-128

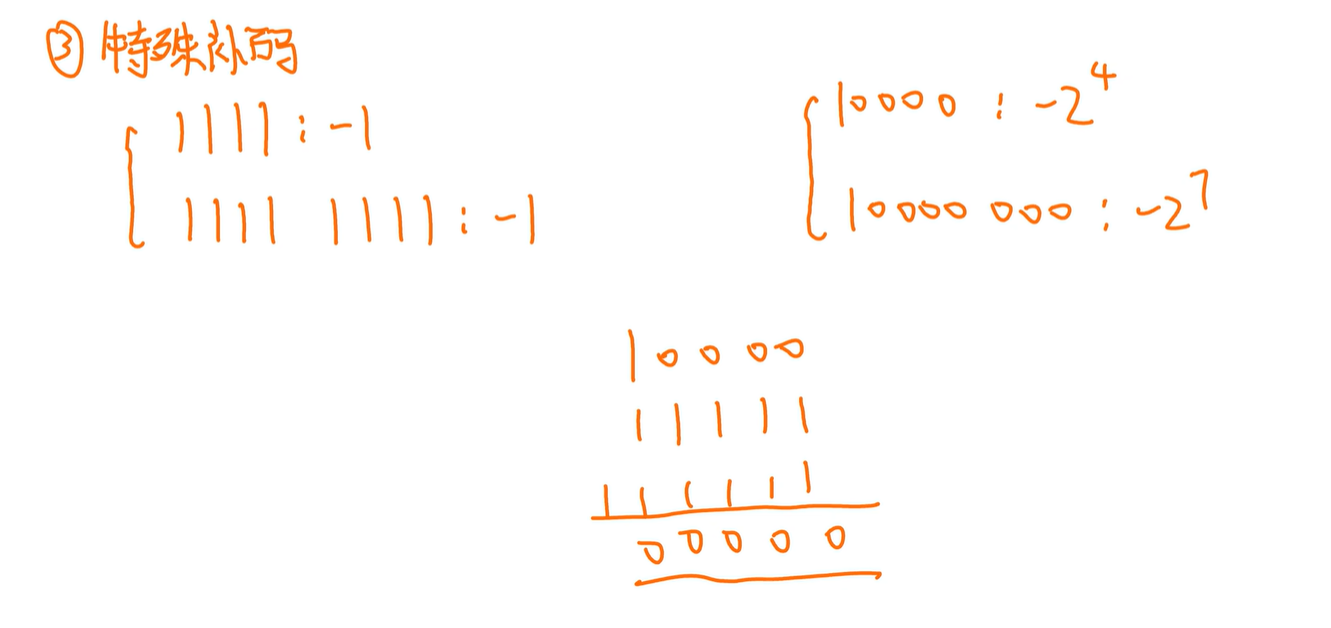
补码全1:原码为-1
(特殊情况)1后面全0:几个0,就是-2的几次方
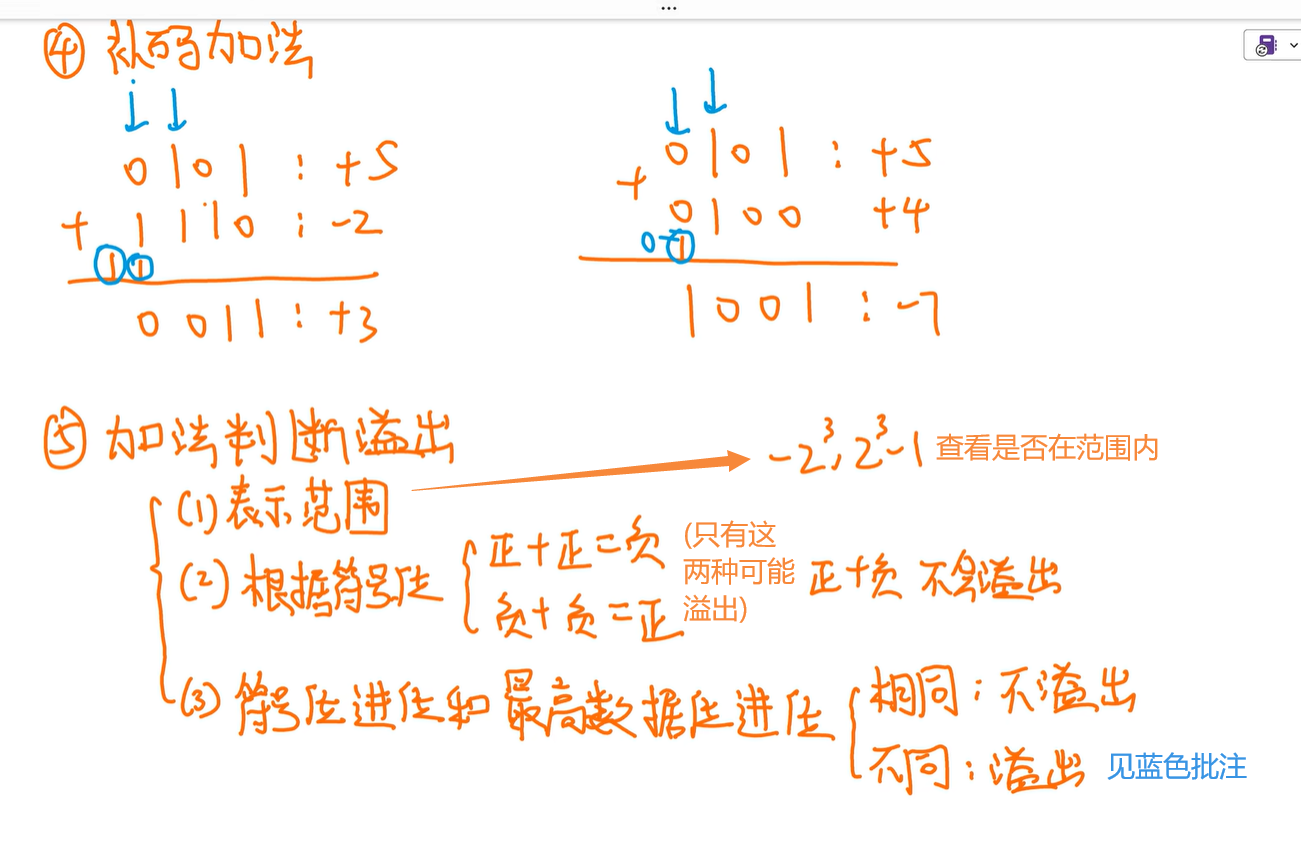
补码相加,符号位可以参与运算,但要判断
注意:判断溢出时,若使用方法(3)进位来判断,不能用十六位看,要看转成二进制后看进位

① 变符号位
② 再按转补码规则变补码
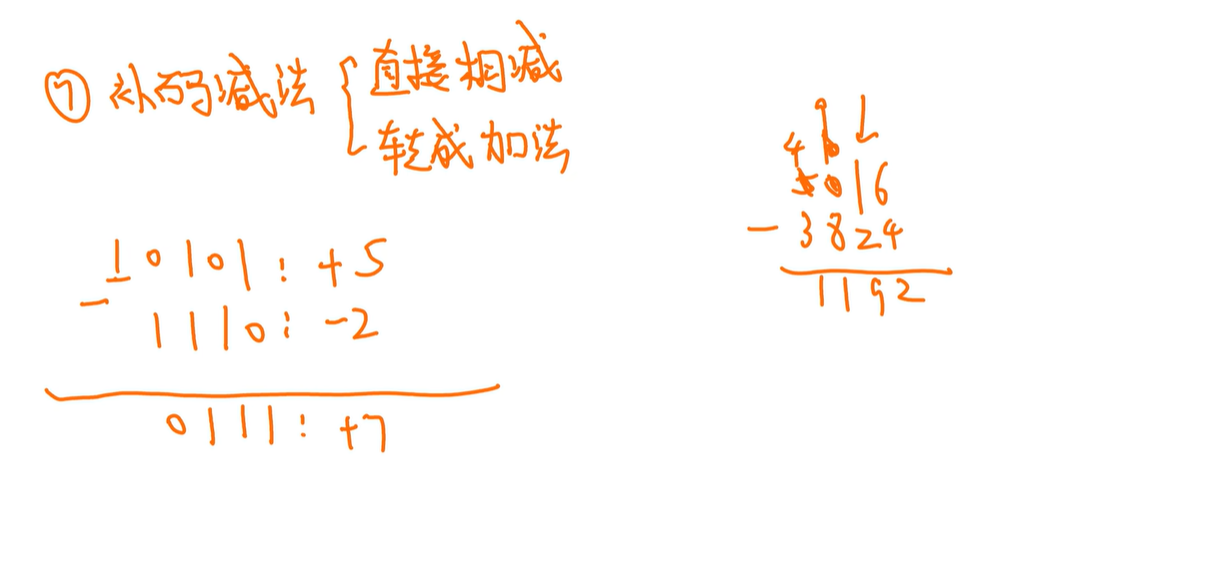
0101-1110
类比十进制减法
最高位都不够借位,可以认为前面有个1,算完之后不要最高位
补码相减,符号位也可以参与运算,但依旧要判断溢出
如:
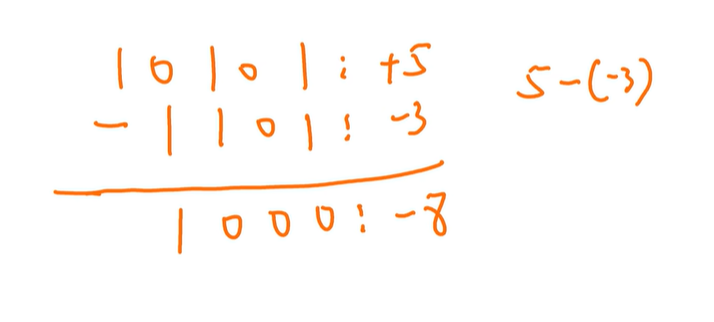


十六进制+ 谁,能变成1后面全0,加的这个数就是它的绝对值
有的时候常规方法更好用
这种方法要注意区分正负:
正数直接算就行
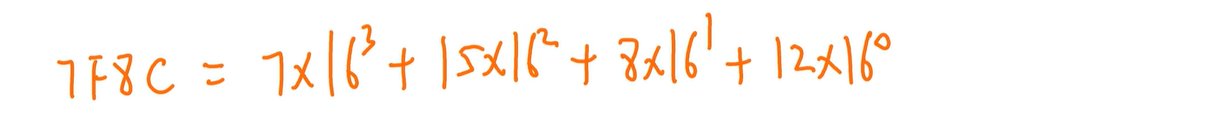
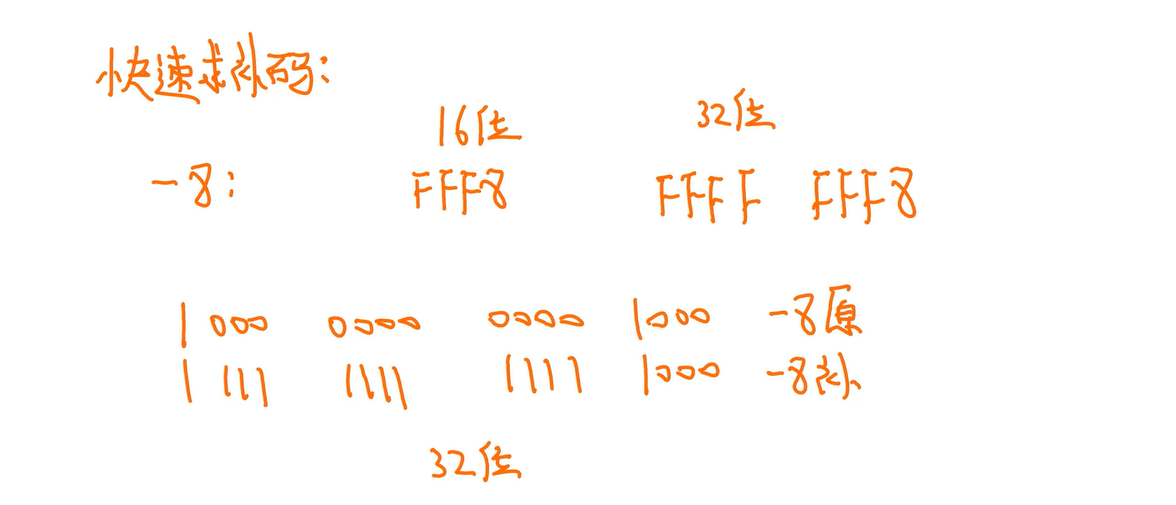
反过来,十进制原码 + 十六进制的谁,能变成1后面全0,加的这个数就是它的补码。
数字比较小时好用
又一例:
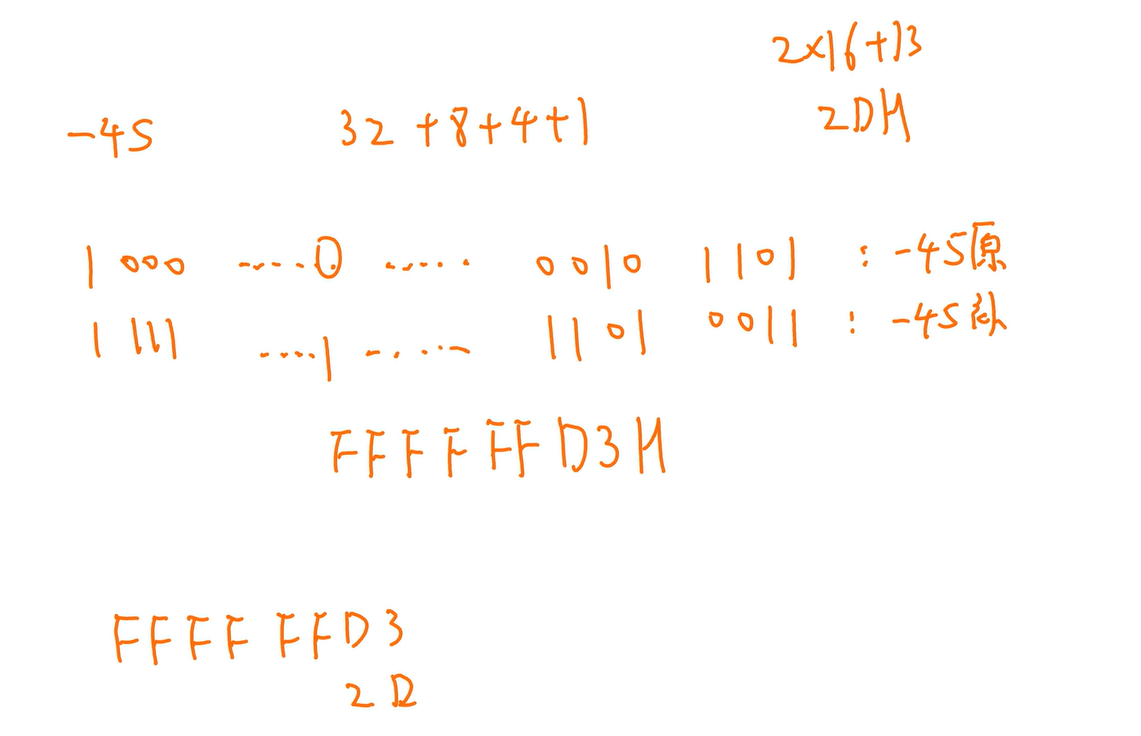
小结及补充
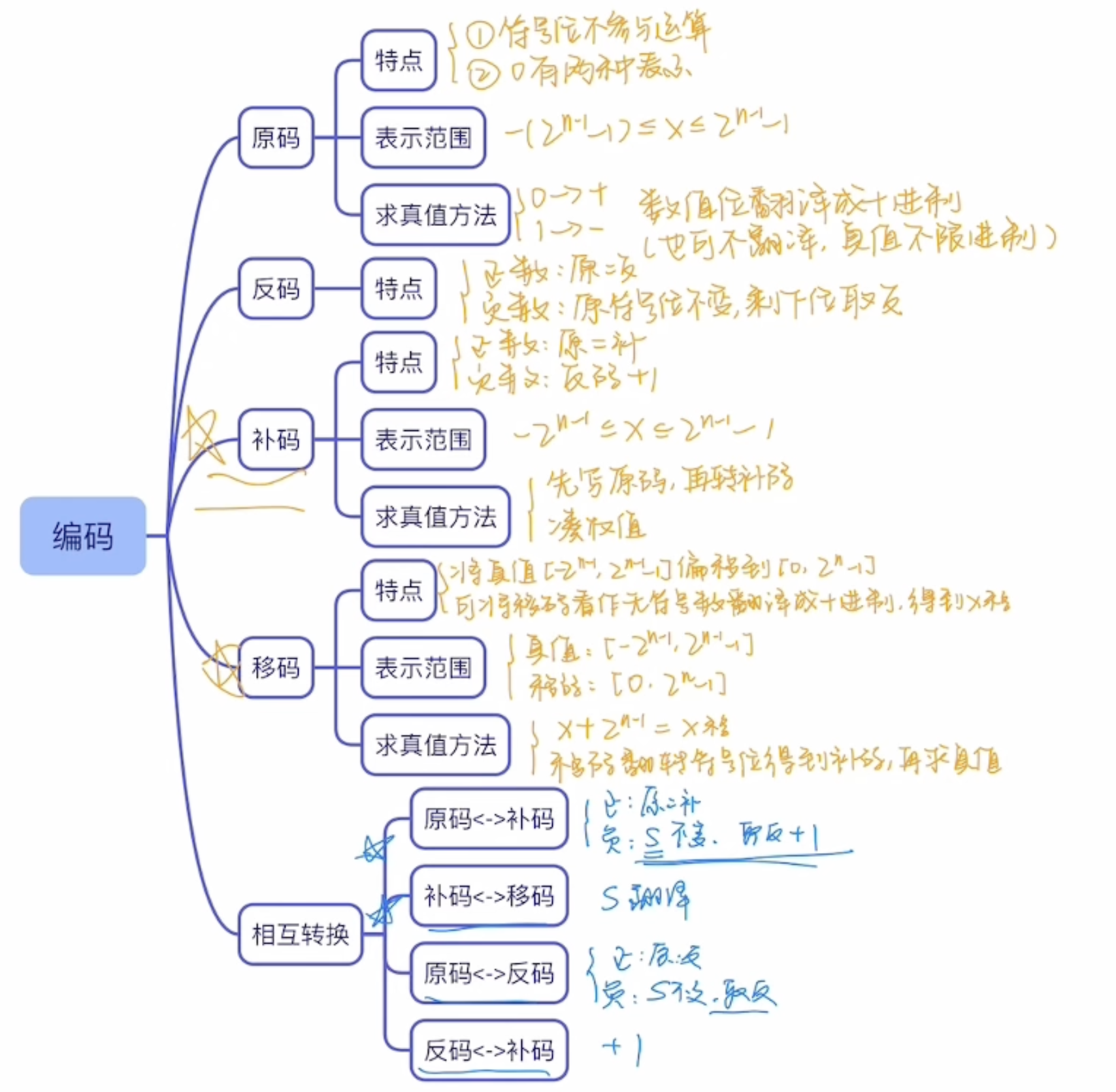
e.g.: 63/32 不要写成小数,想到63/$2^5$,移位(右移)
例:

注意:最高位进位出去了,不代表一定溢出
无符号数和有符号数
有符号数
第一位 1 -; 0+
类型转换
无符号数和有符号数的转换
机器数不变,加上符号,真值变
例:p31 表2.1
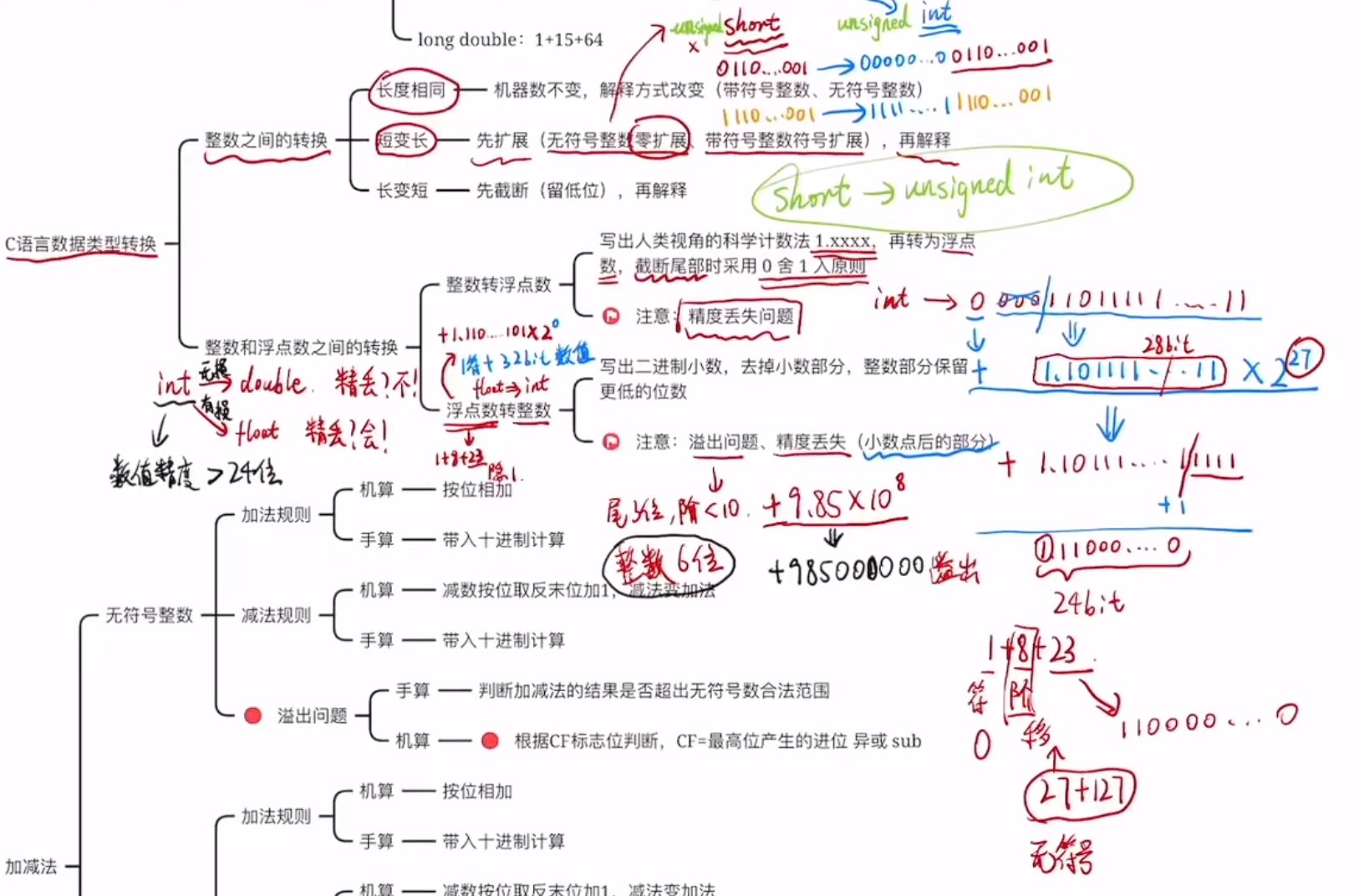
不同字长整数间的转换
大字长->小字长:高位截断,低位赋值
例如:32位--赋-->16位,只保留低16位
小字长->大字长:对高位进行扩展——零扩展和符号扩展
零扩展:前面补0
符号扩展:前面补符号位(对于原码来说数值不变)
运算方法和运算电路
加法器
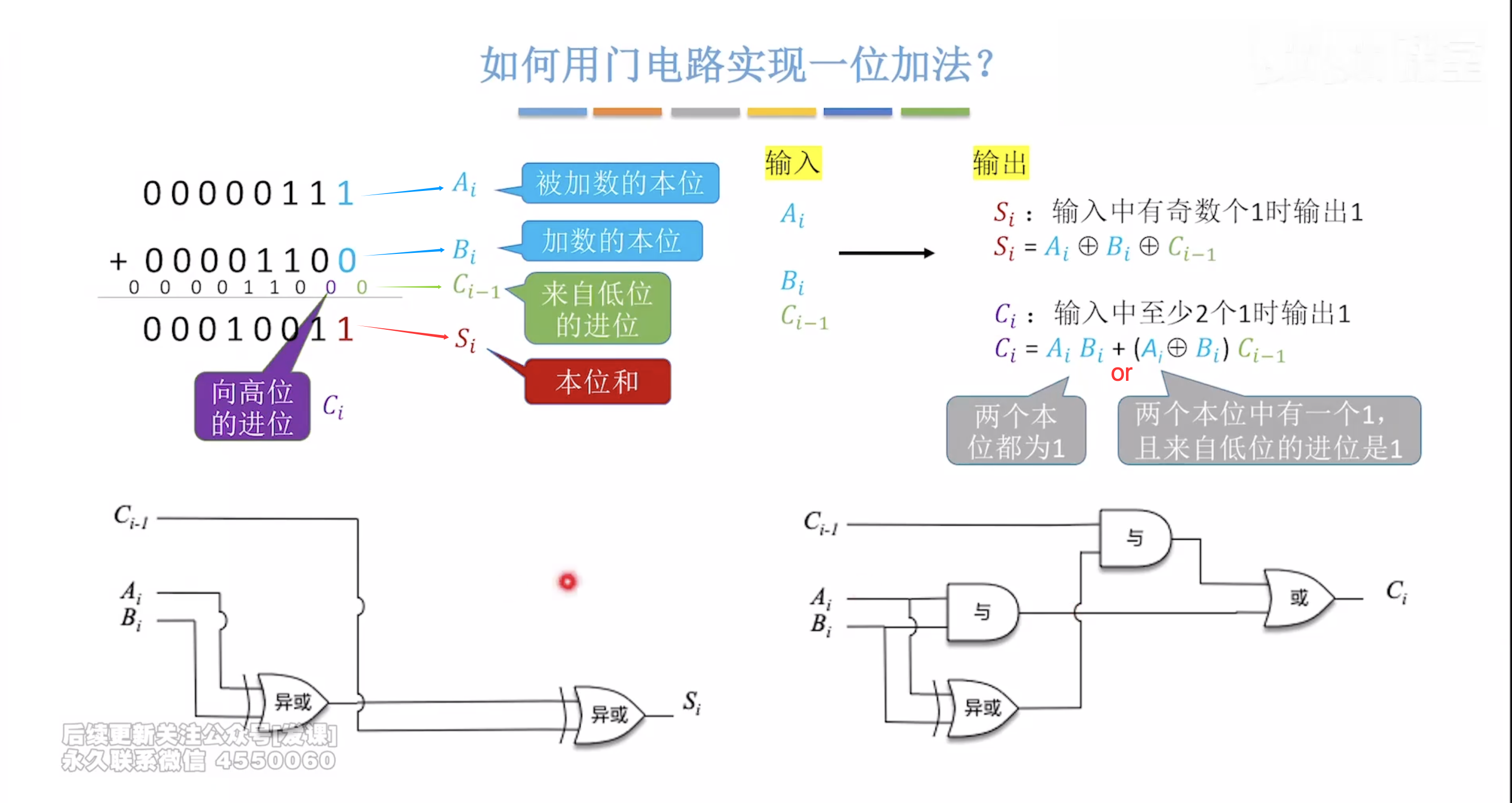
合并这两个电路
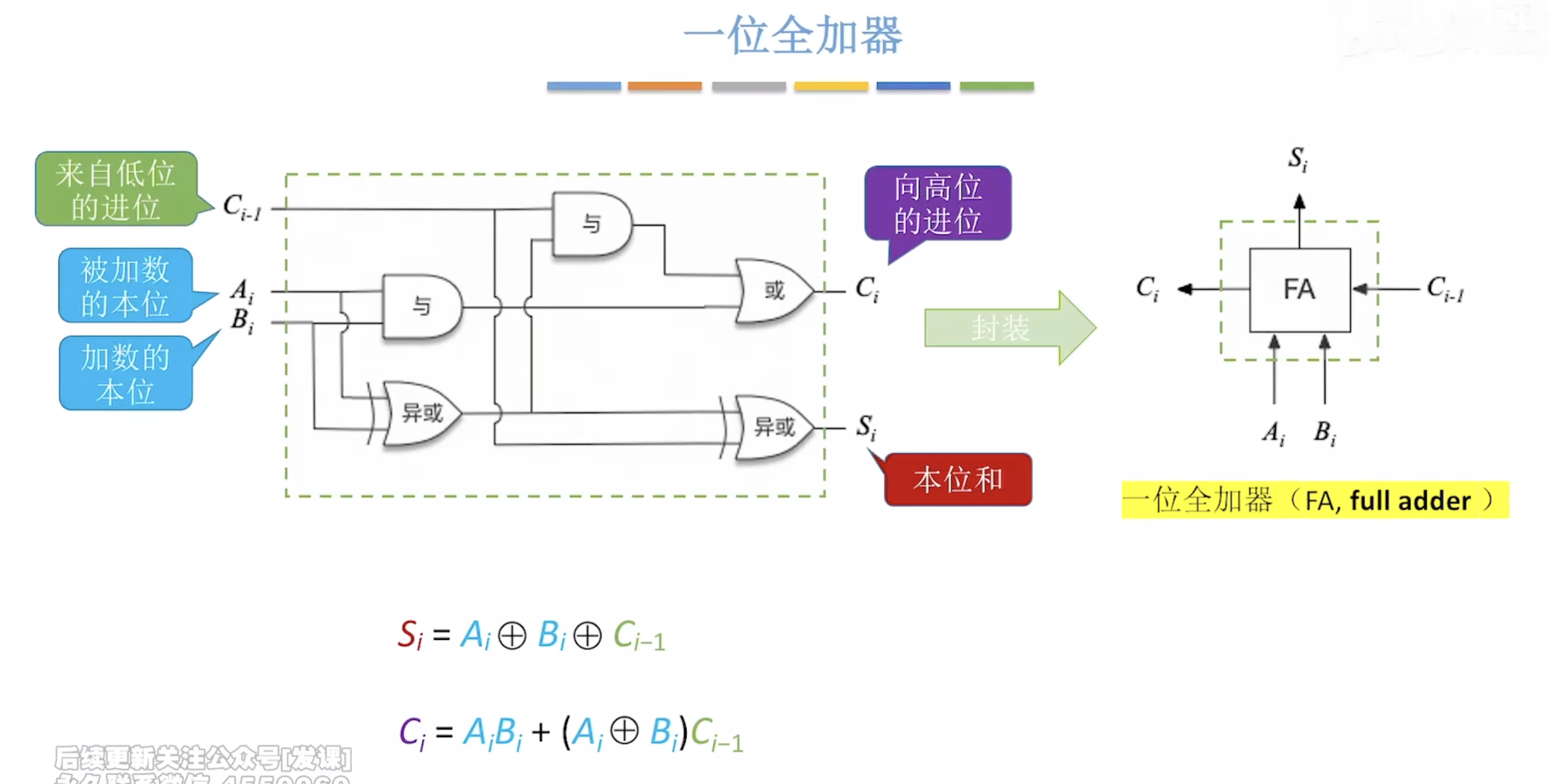
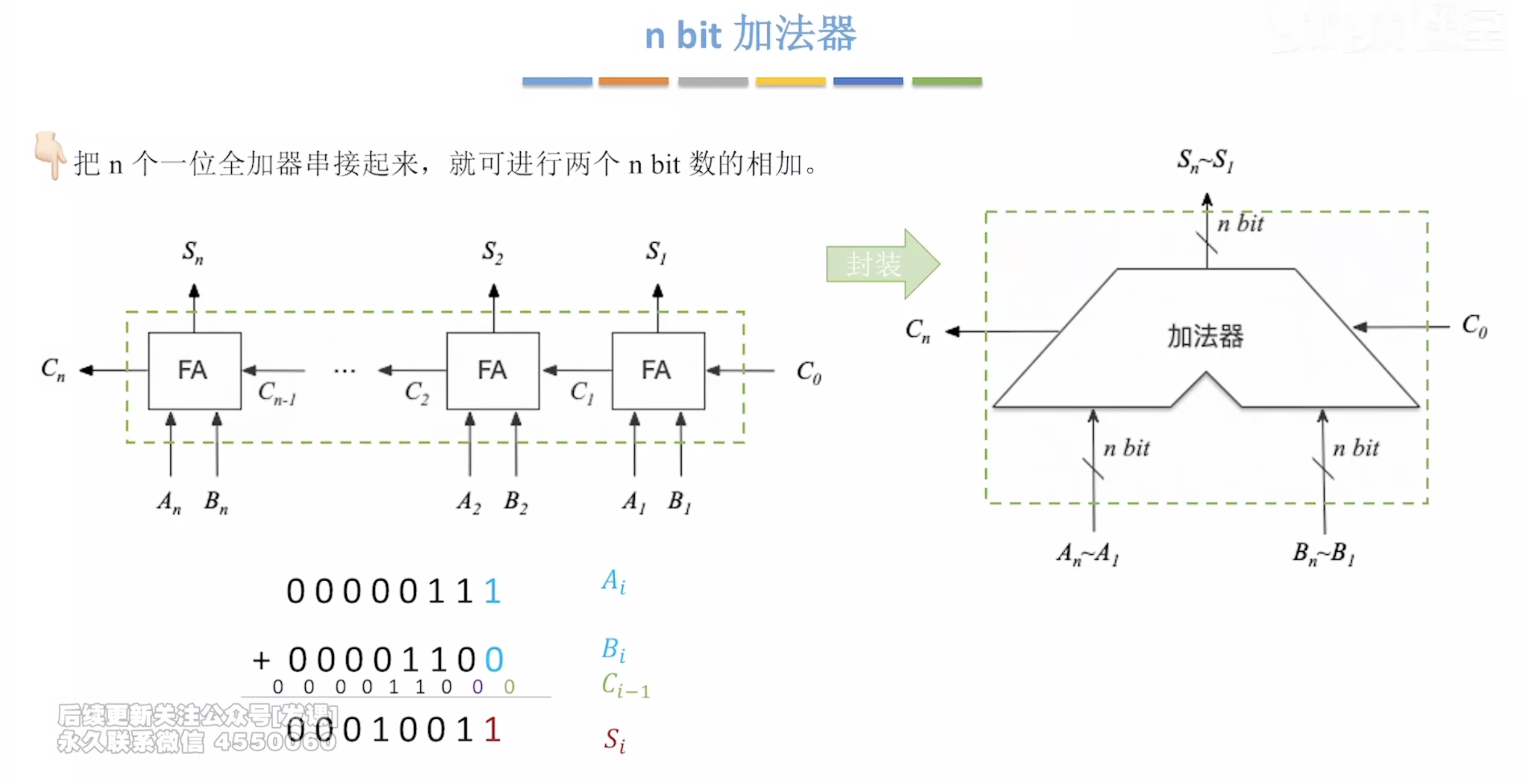
不足:进位信息是串行产生的,计算速度取决于进位产生和传递的速度。位数越多,运算速度越慢
由于两个输入端允许并行输入 nbit,因此这种加法器属于“并行加法器”
由于进位信息是串行产生的,因此从“进位方式”看,这种加法器属于“串行进位加法器”
也可以称为“申行进位的并行加法器”
带标志位的加法器
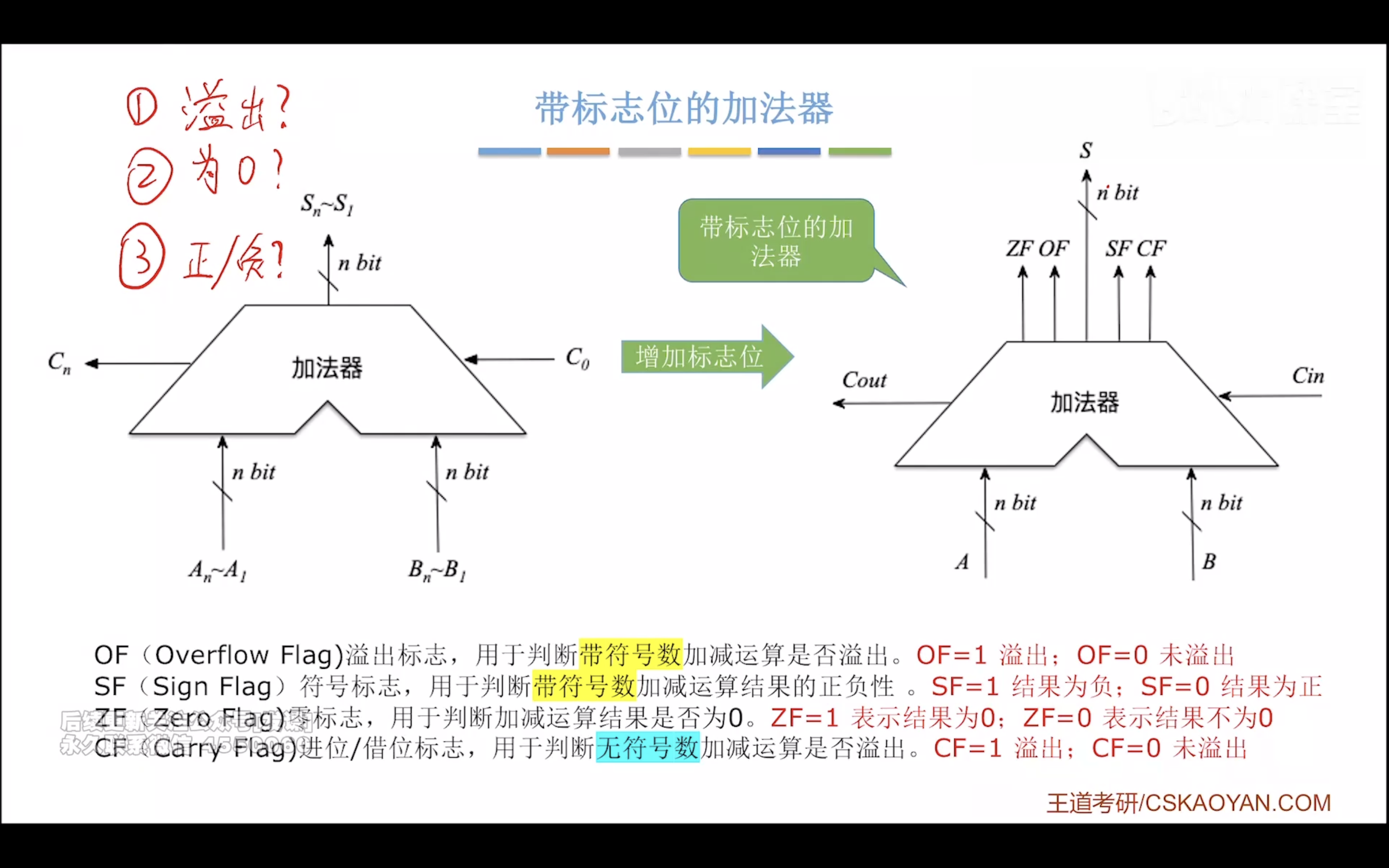
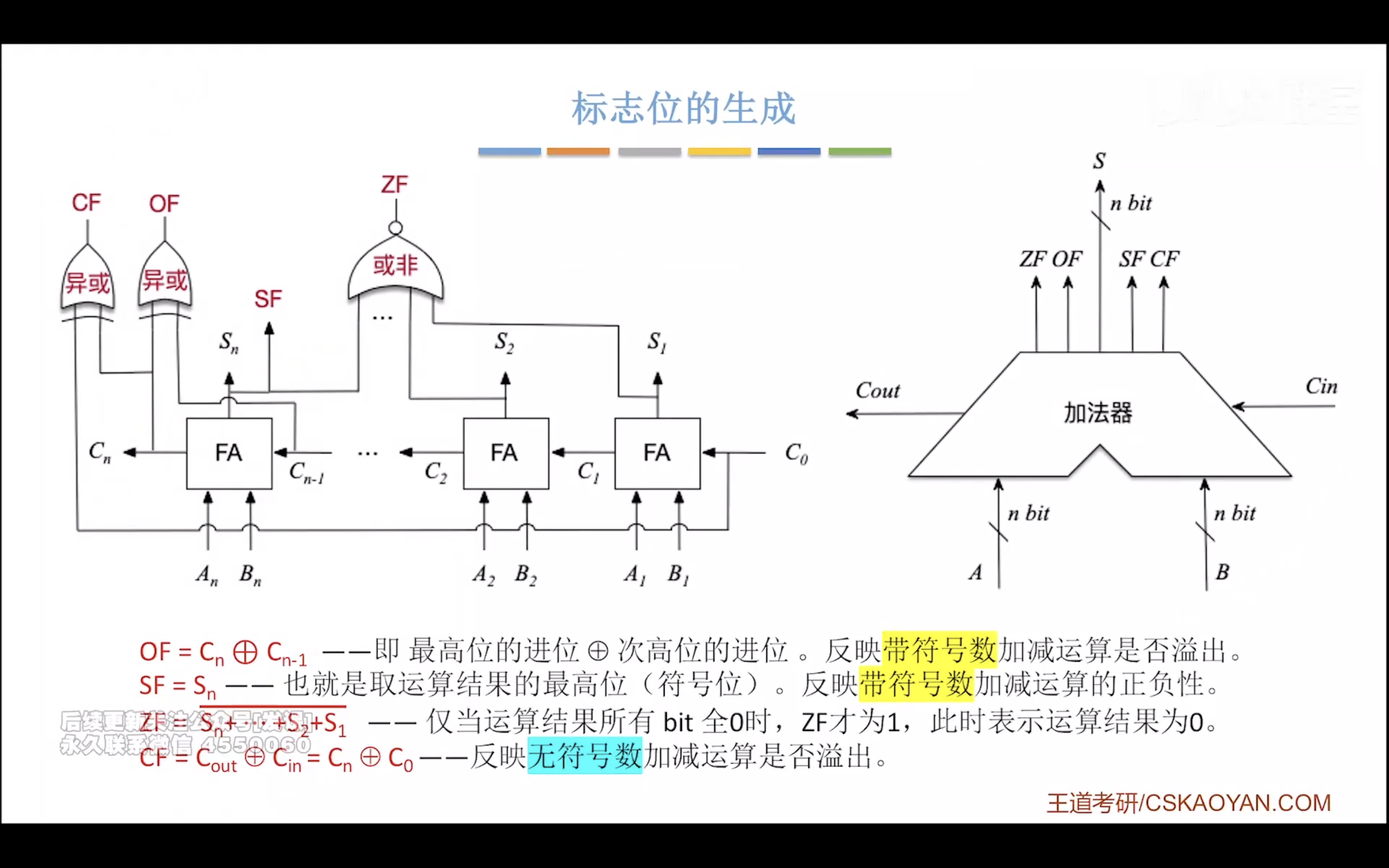
小结
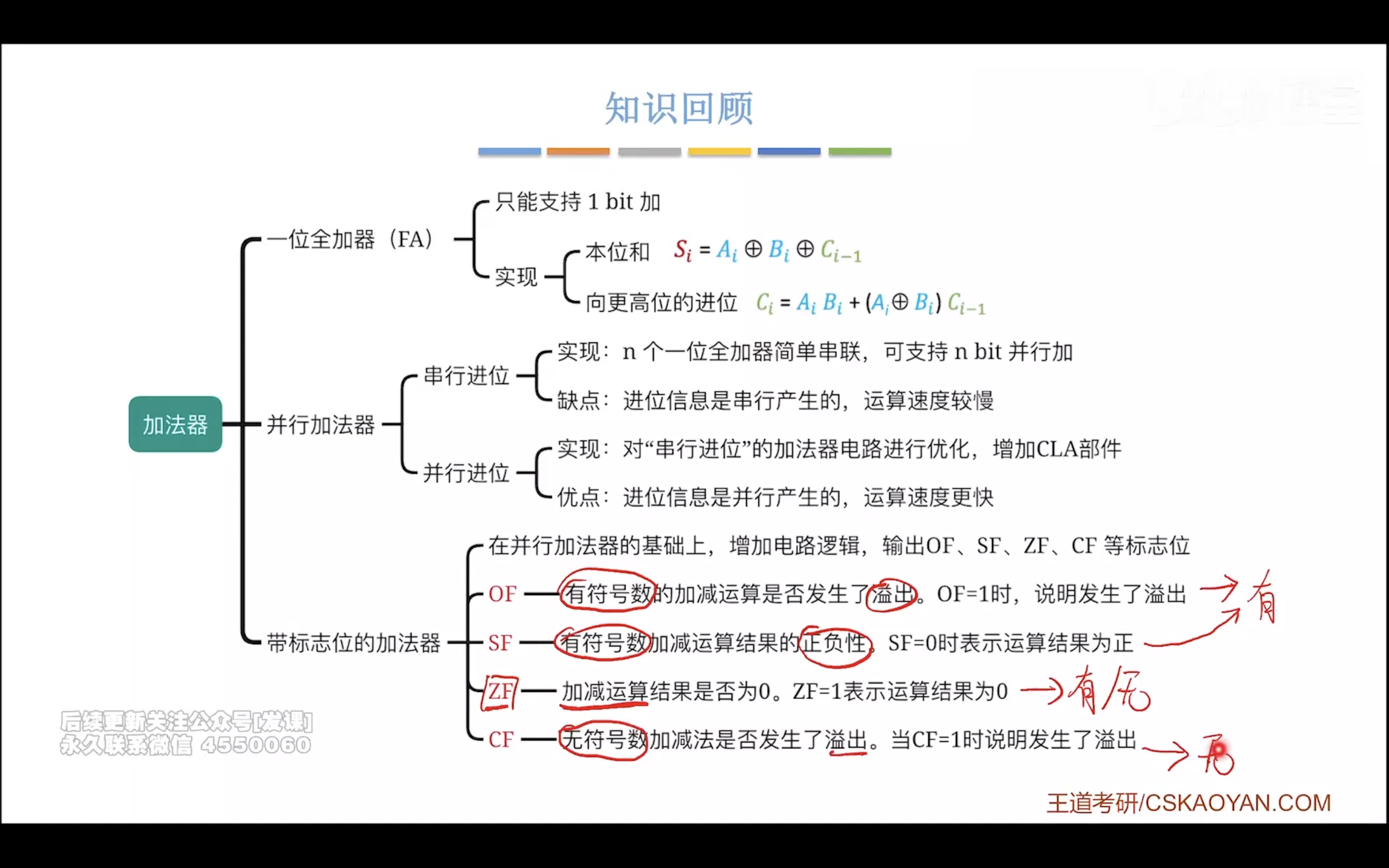
(这部分的电路图不需掌握,ALU的要)
算术逻辑单元 ALU
PSW:程序状态寄存器

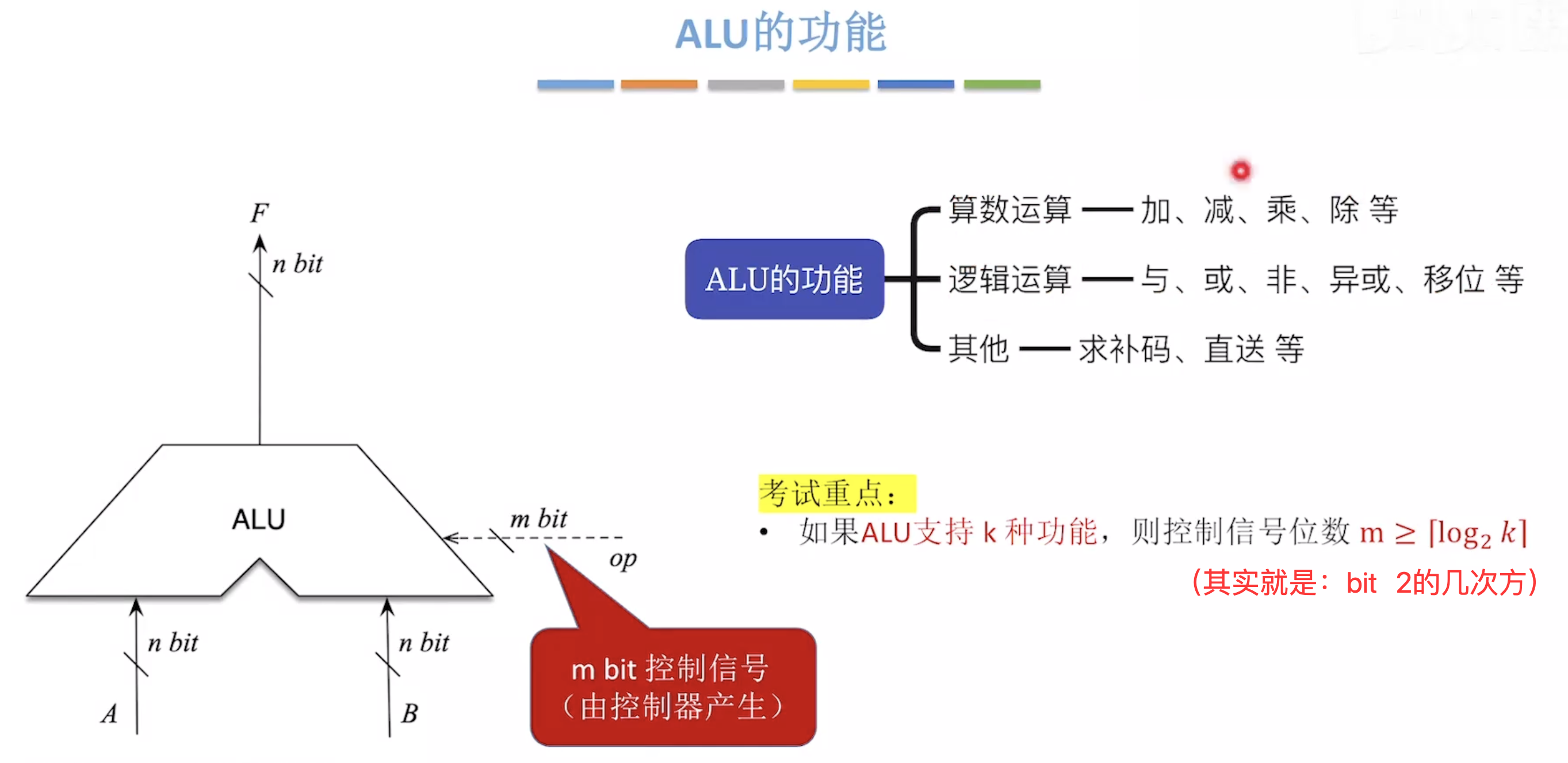
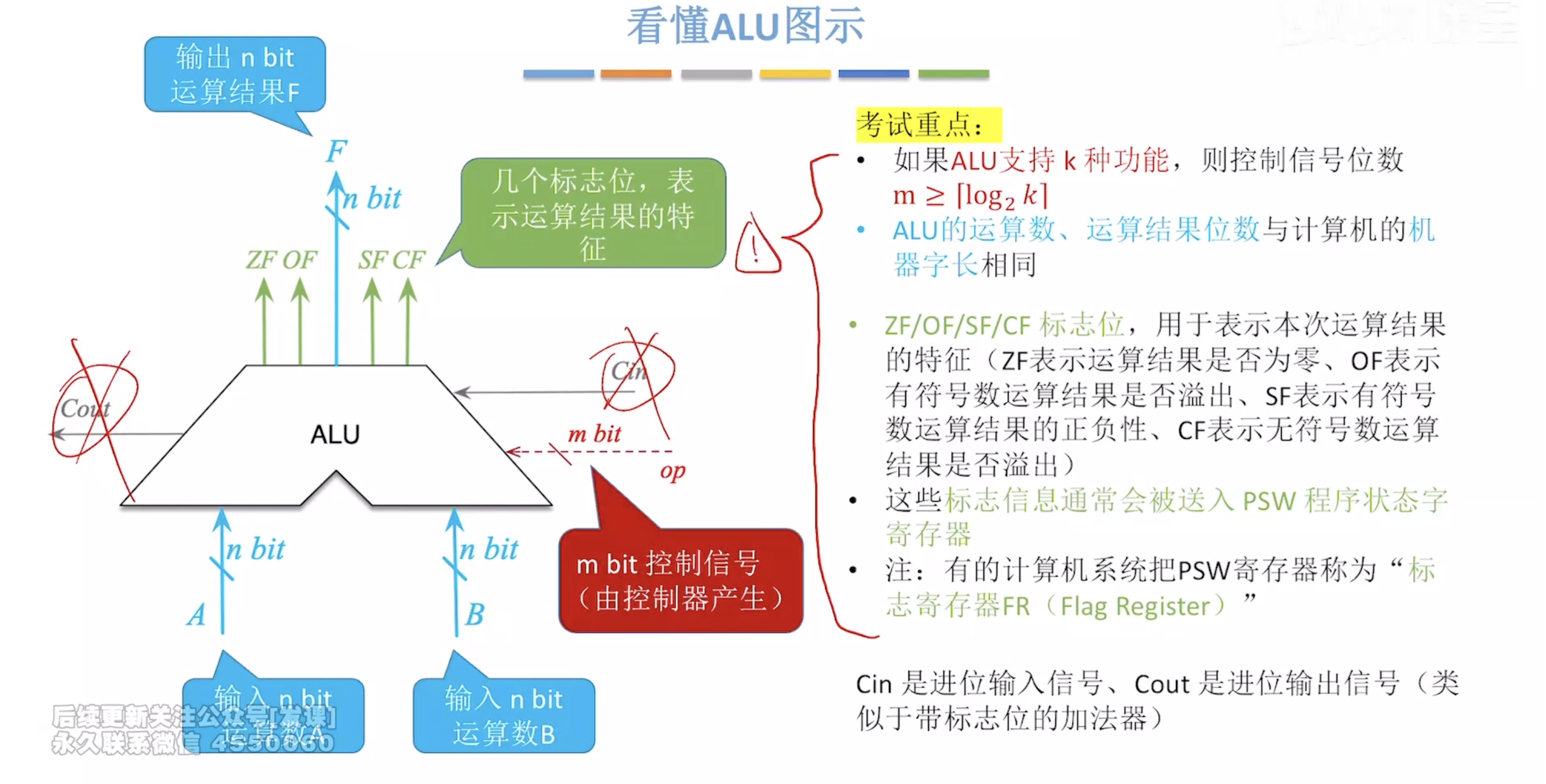
计算机字长由ALU运算数决定
e.g.:
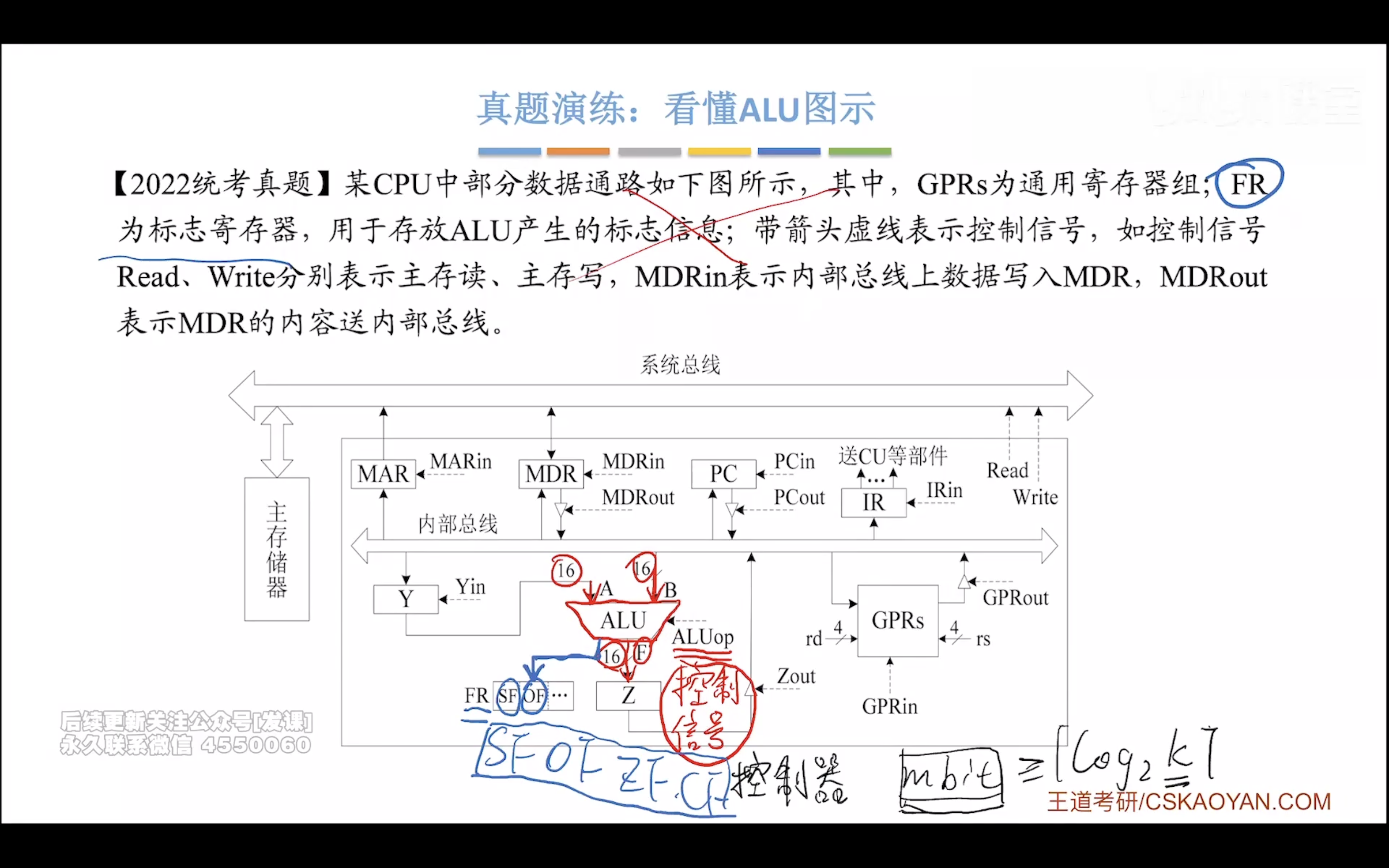
小结
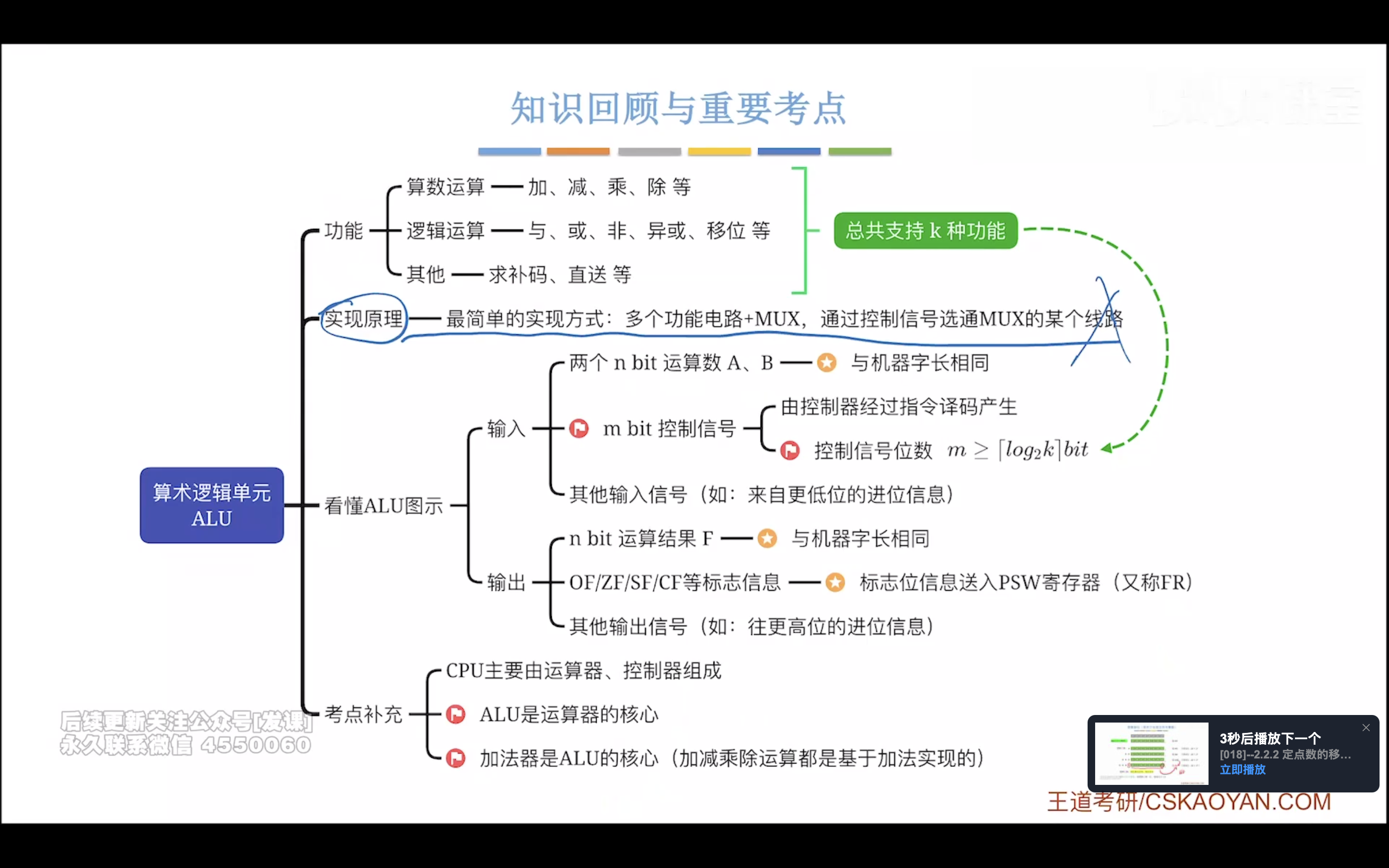
定点数的移位计算
移位是把数据相对于小数点进行移动
逻辑移位
缺的补0
算数移位
缺的左边补符号位,右边补0
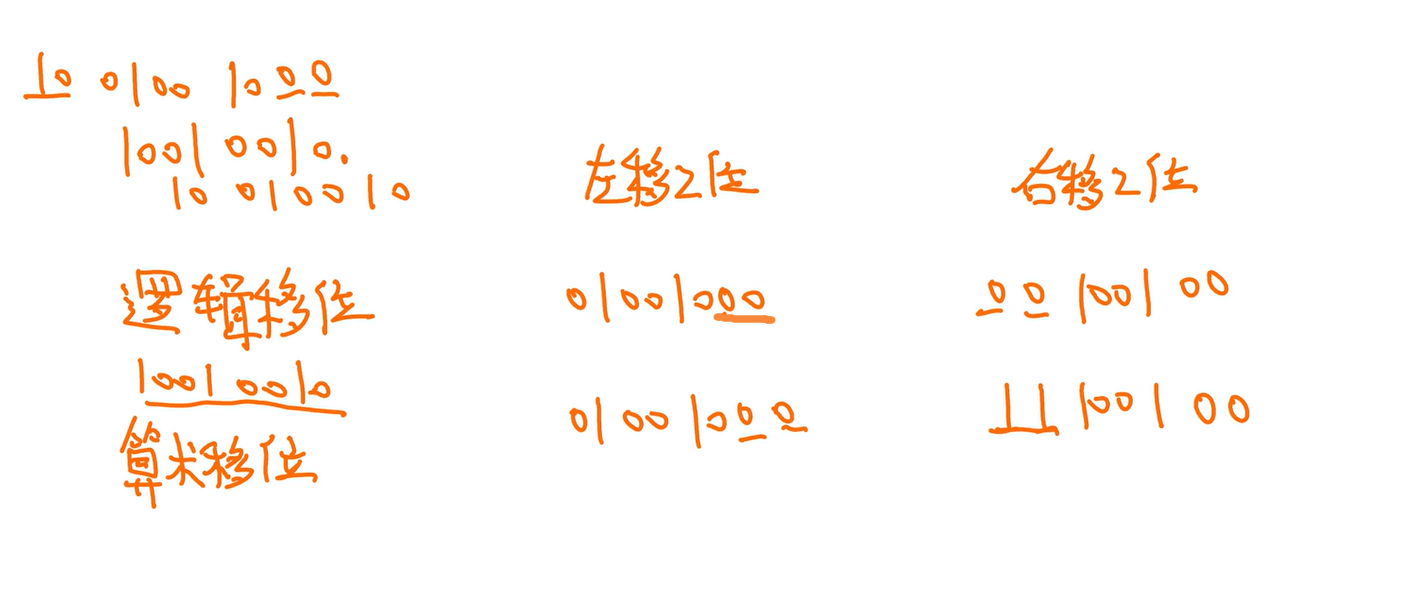
移位的意义
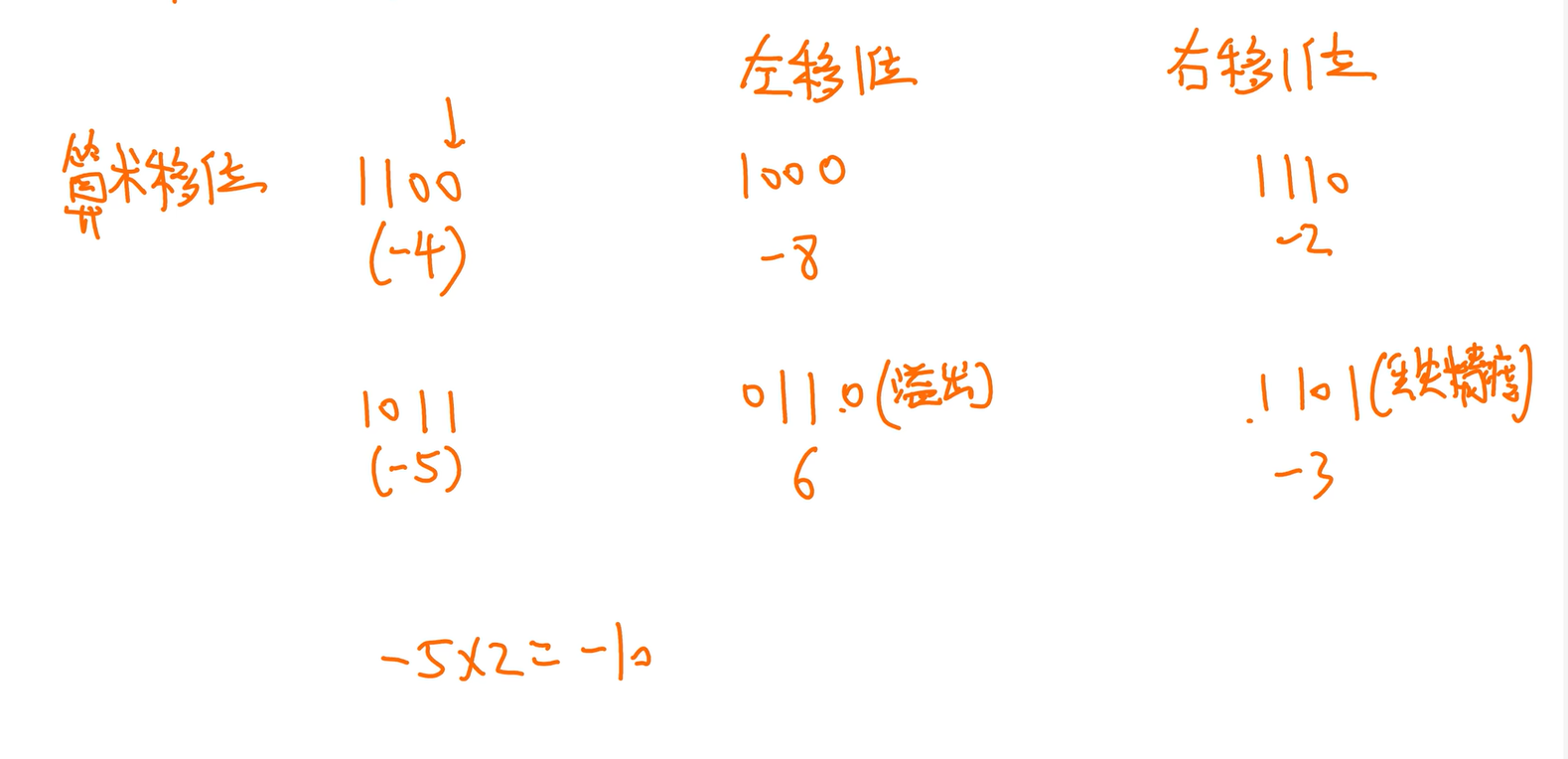
左移:*2,或溢出(移动后符号位变了就溢出)
右移:/2,或丢失精度
以十进制为类比来理解:
只能存4位时
1234左移2位,只能存4位:本该是123400,结果是3400
右移2位:本该是12.34,结果是0012
算术移位判断溢出:左移被移出的若有和符号位不同的,就会溢出。右移不会溢出,只有1被移出会影响精度
逻辑左移判断溢出:若高位的1移除,则发生溢出
定点数的加减计算
加减运算电路
标志位:ZF OF SF CF
书p43
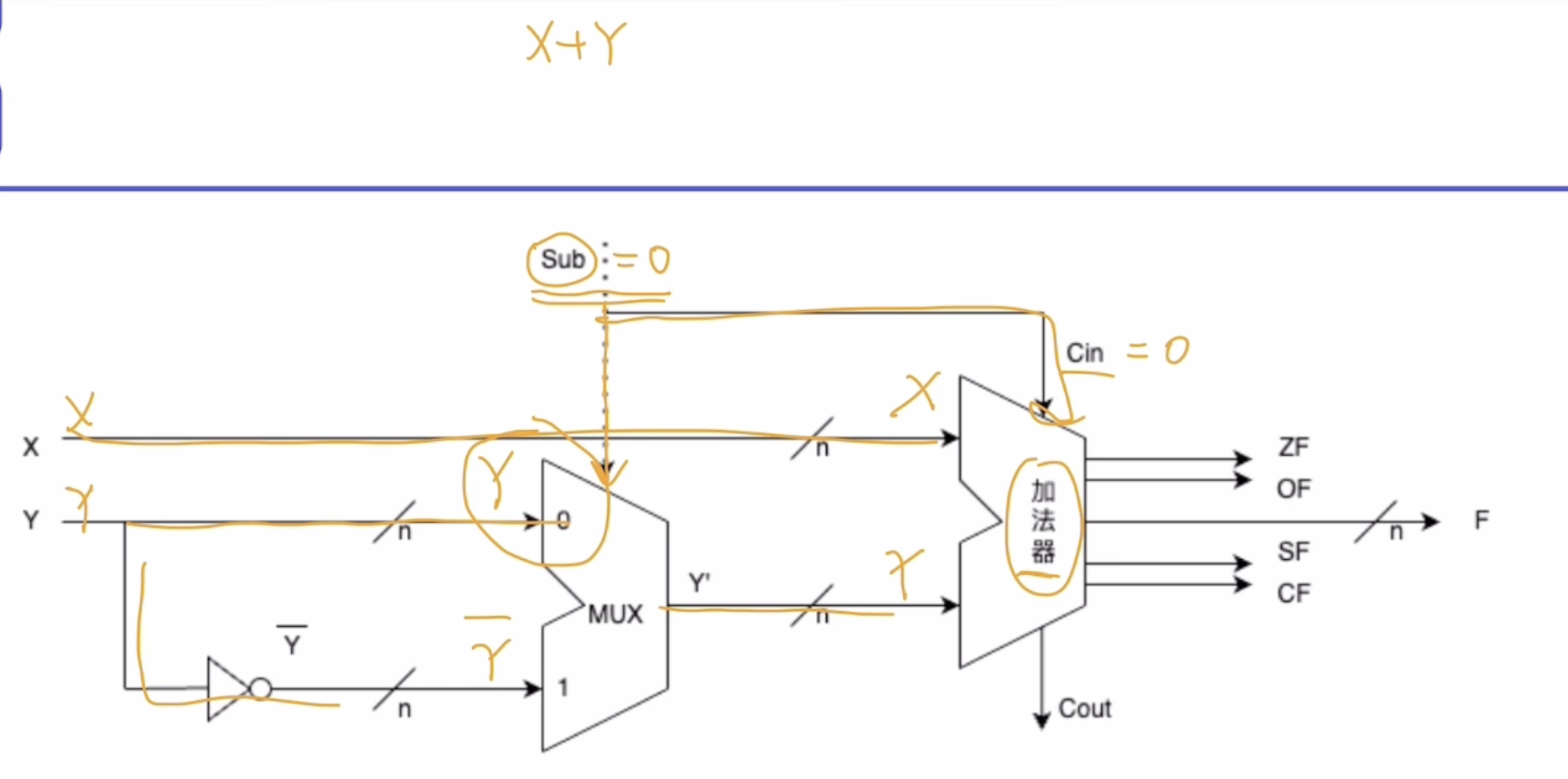
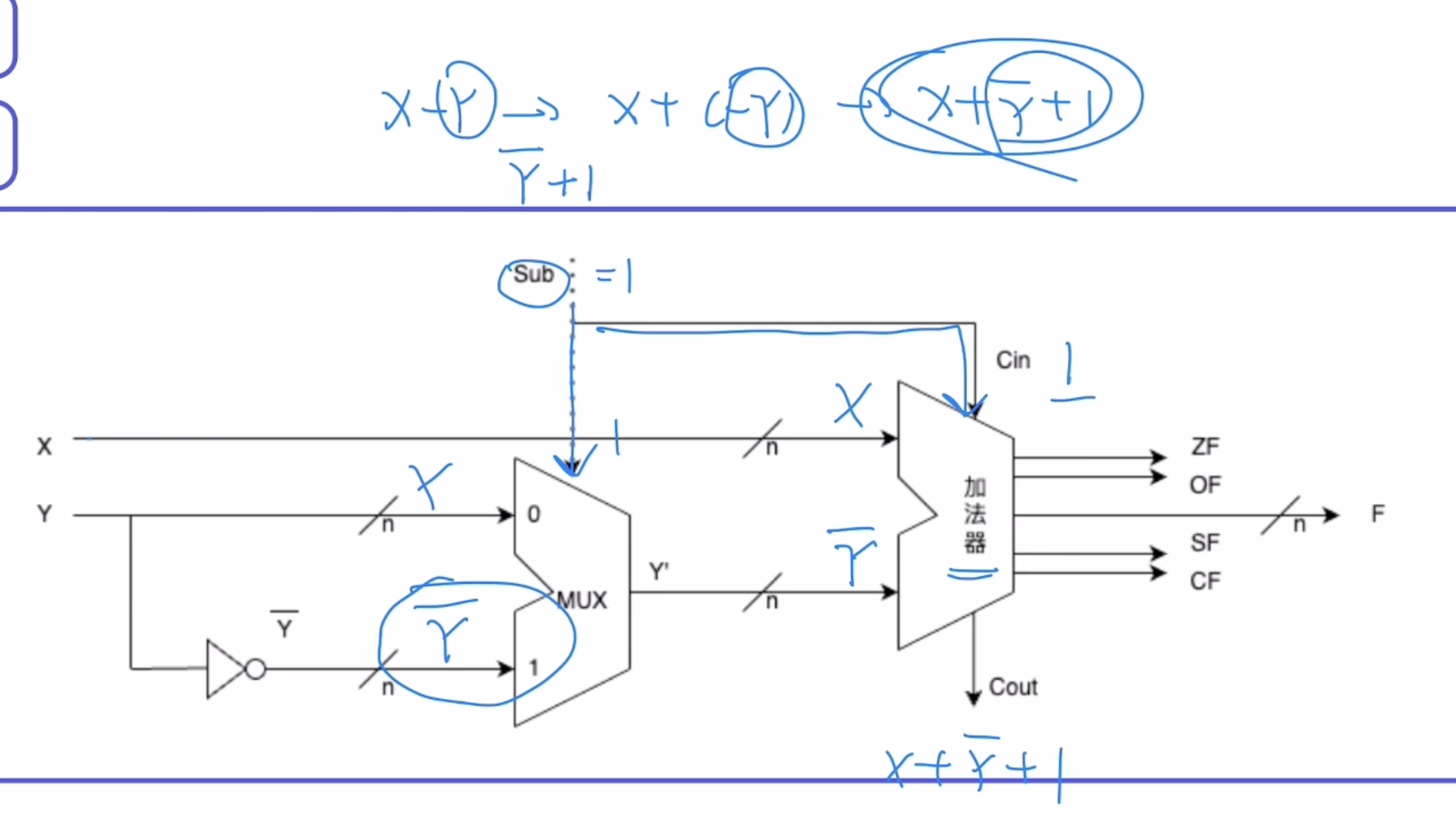
ZF、OF、SF、CF被存放在PSW中,所有人都可见
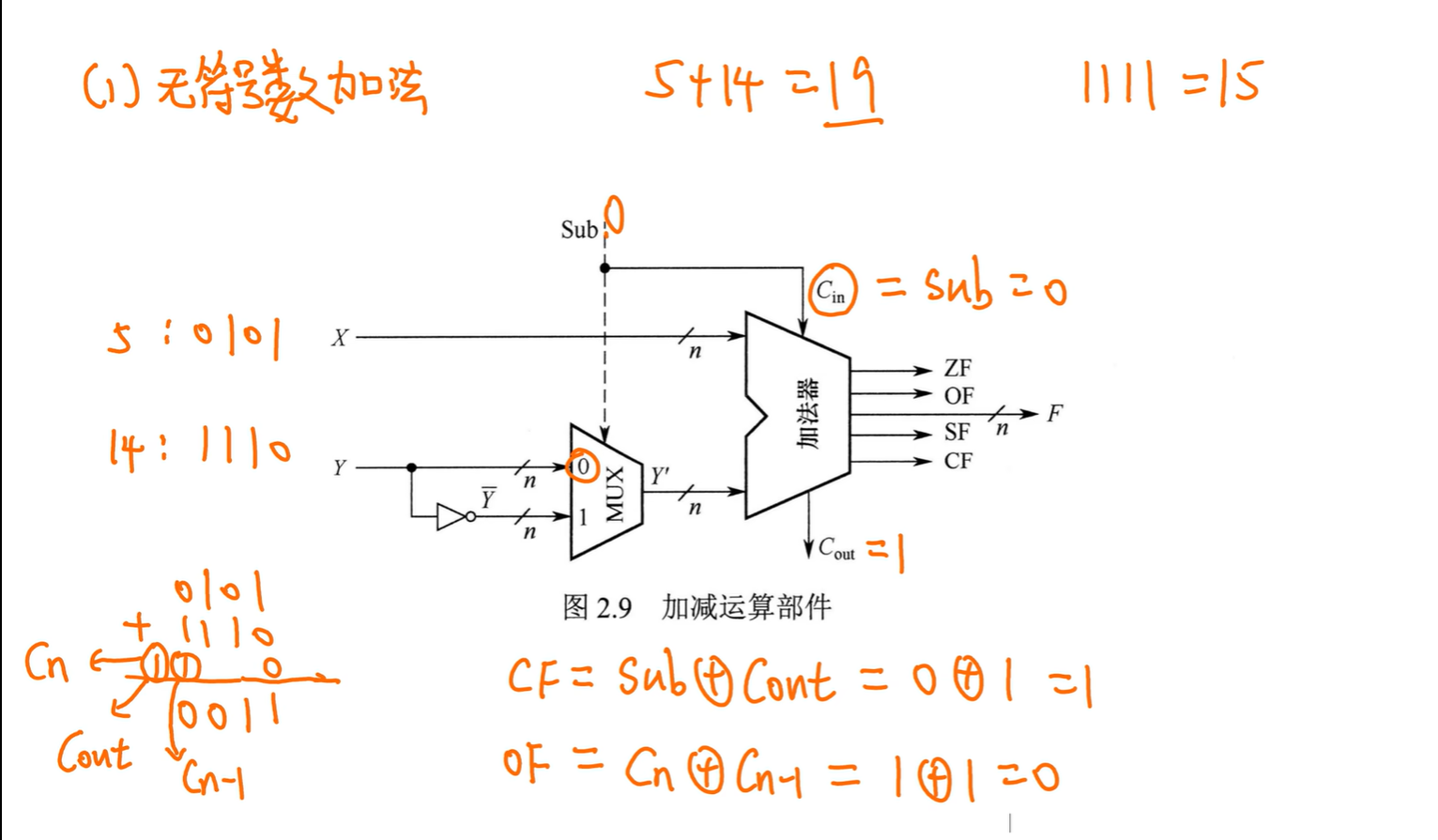
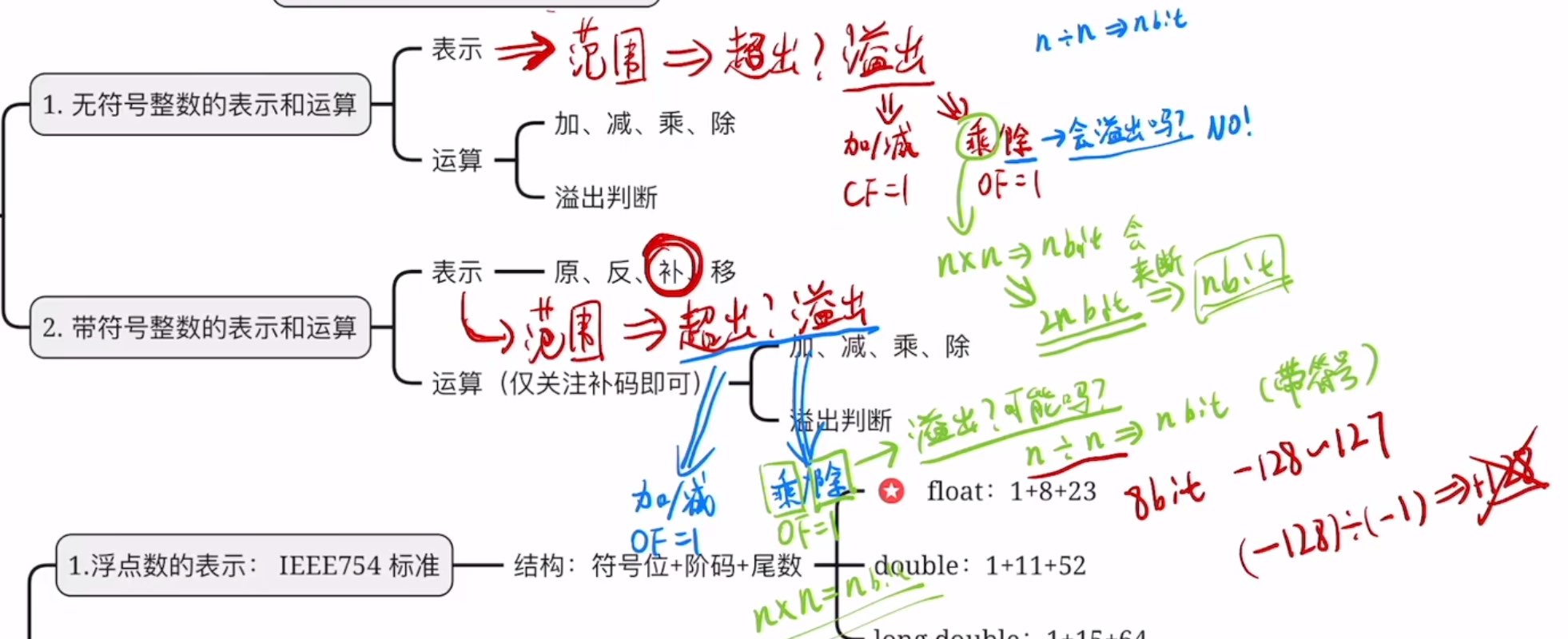
无符号数只看CF
CF=1,表示进位,溢出
OF无意义
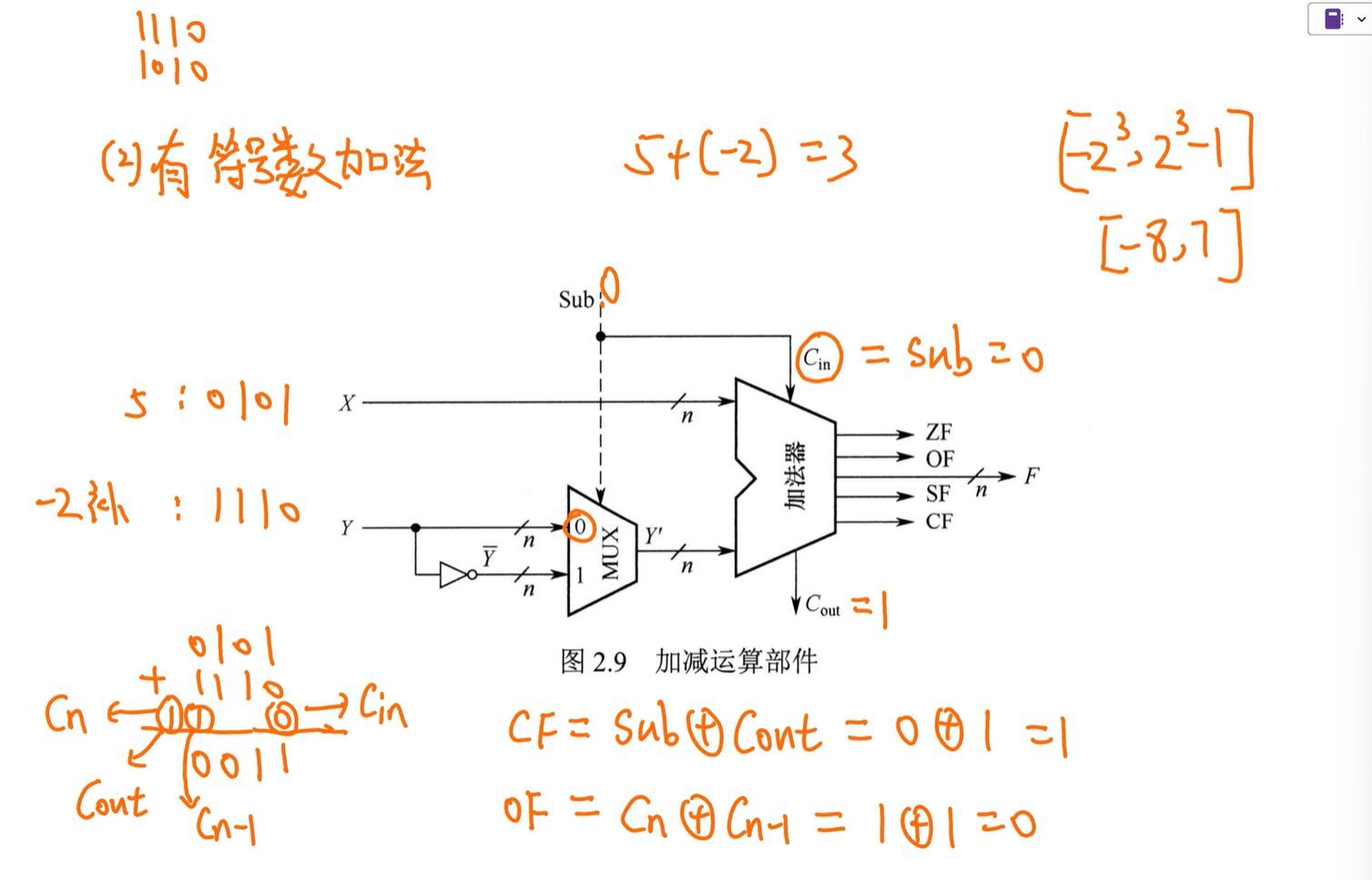
有符号数只看OF
OF=0说明没溢出
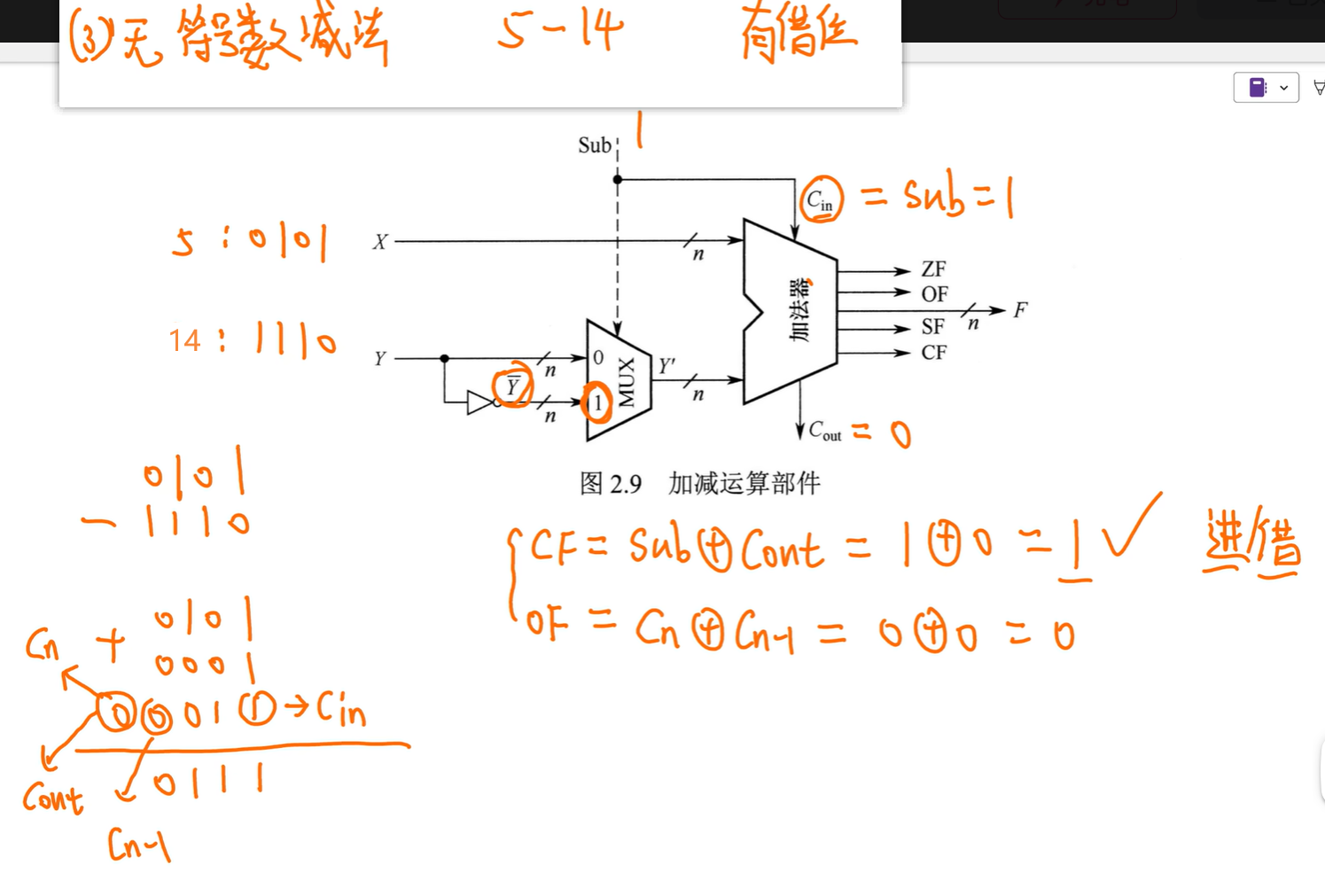
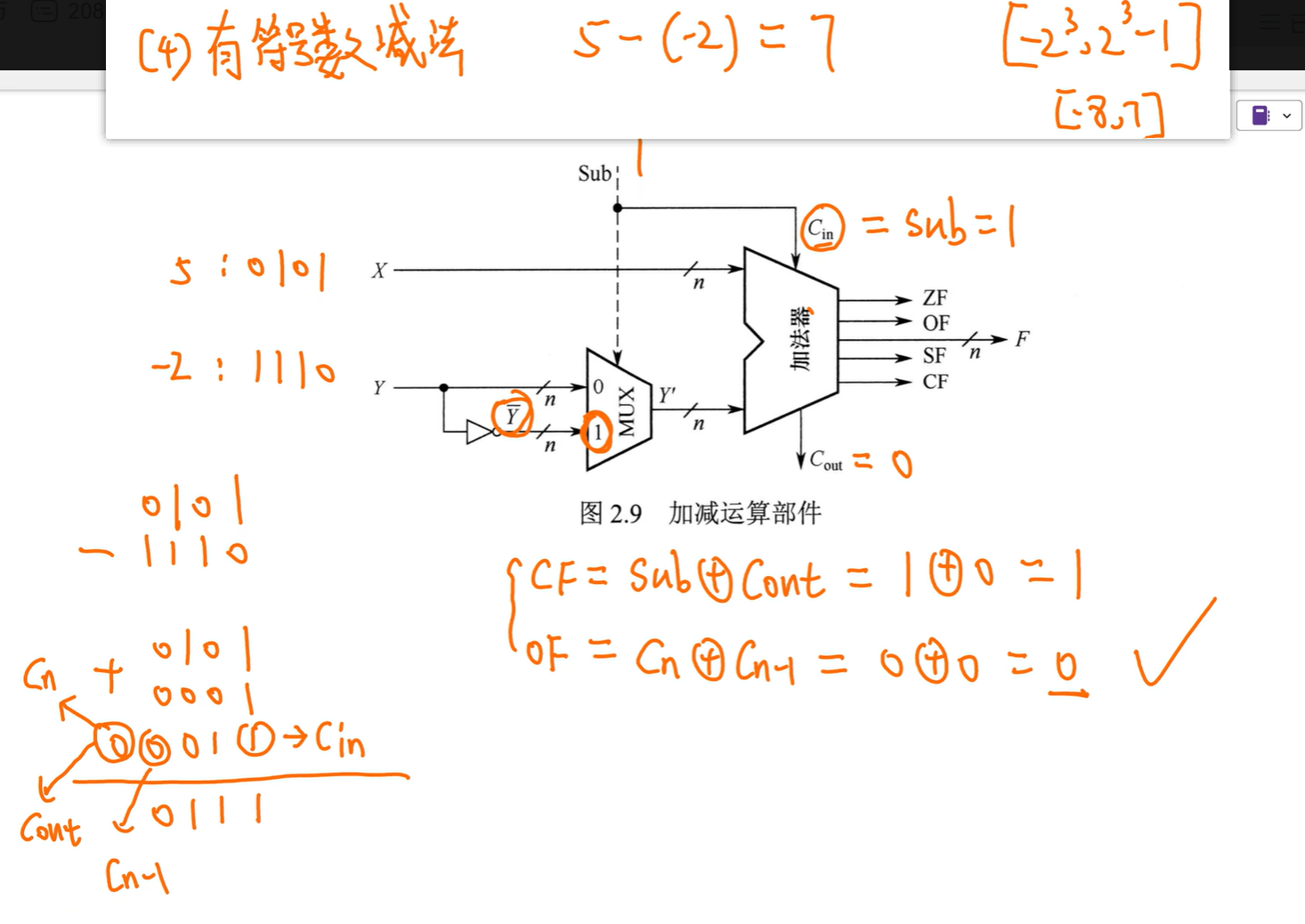
机器数一样,$C{in}$、$C{out}$ 、$Cn$、$C{n-1}$都一样,但表示的值不一样,因为有符号数存的是补码
可以这样理解记忆(结果论):
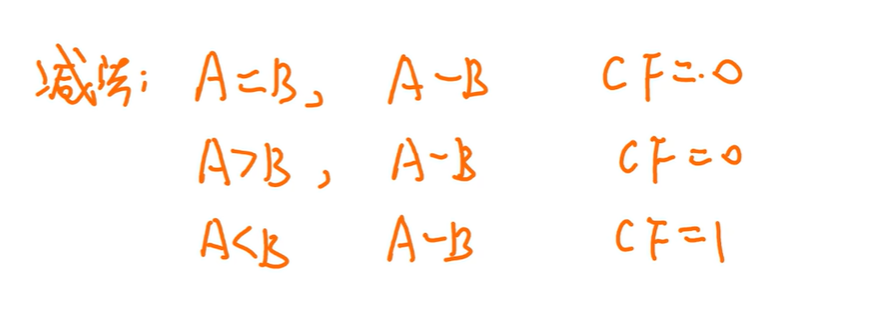
小结
带符号数才叫溢出,无符号数叫进位借位
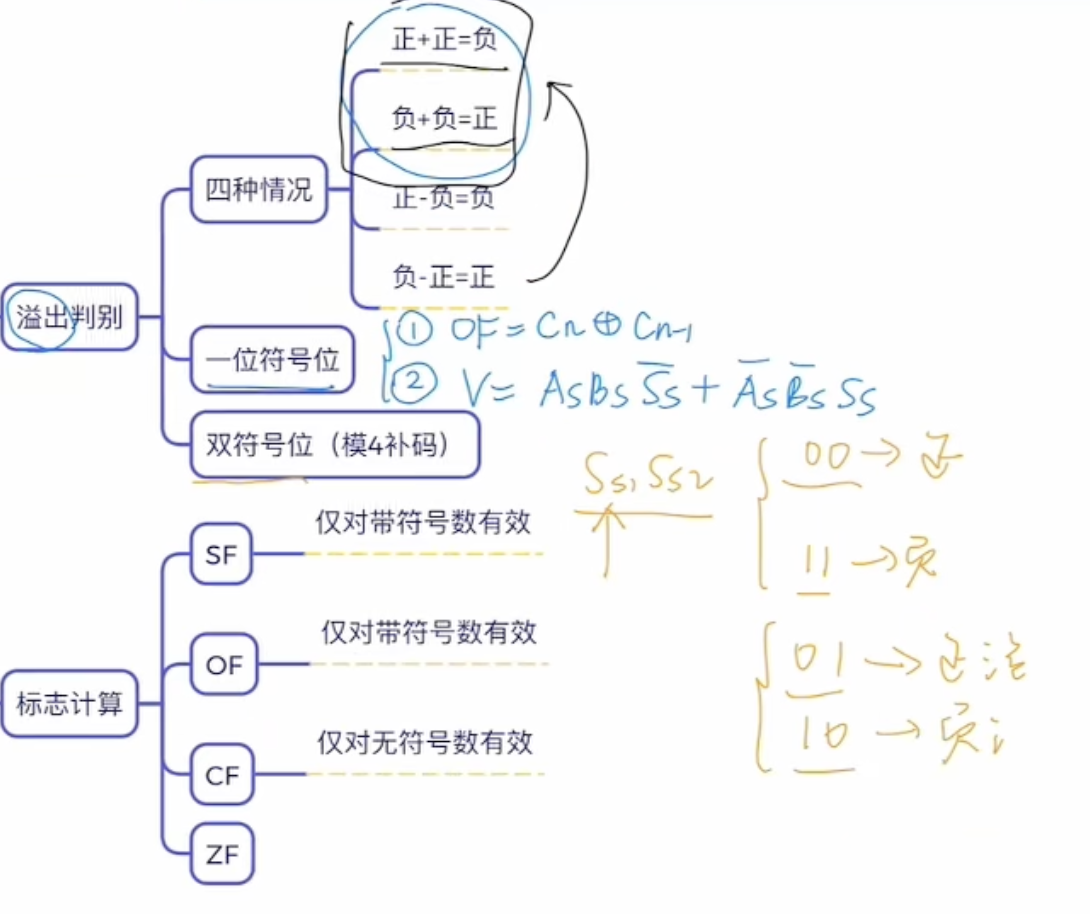
定点数的乘除运算
乘法
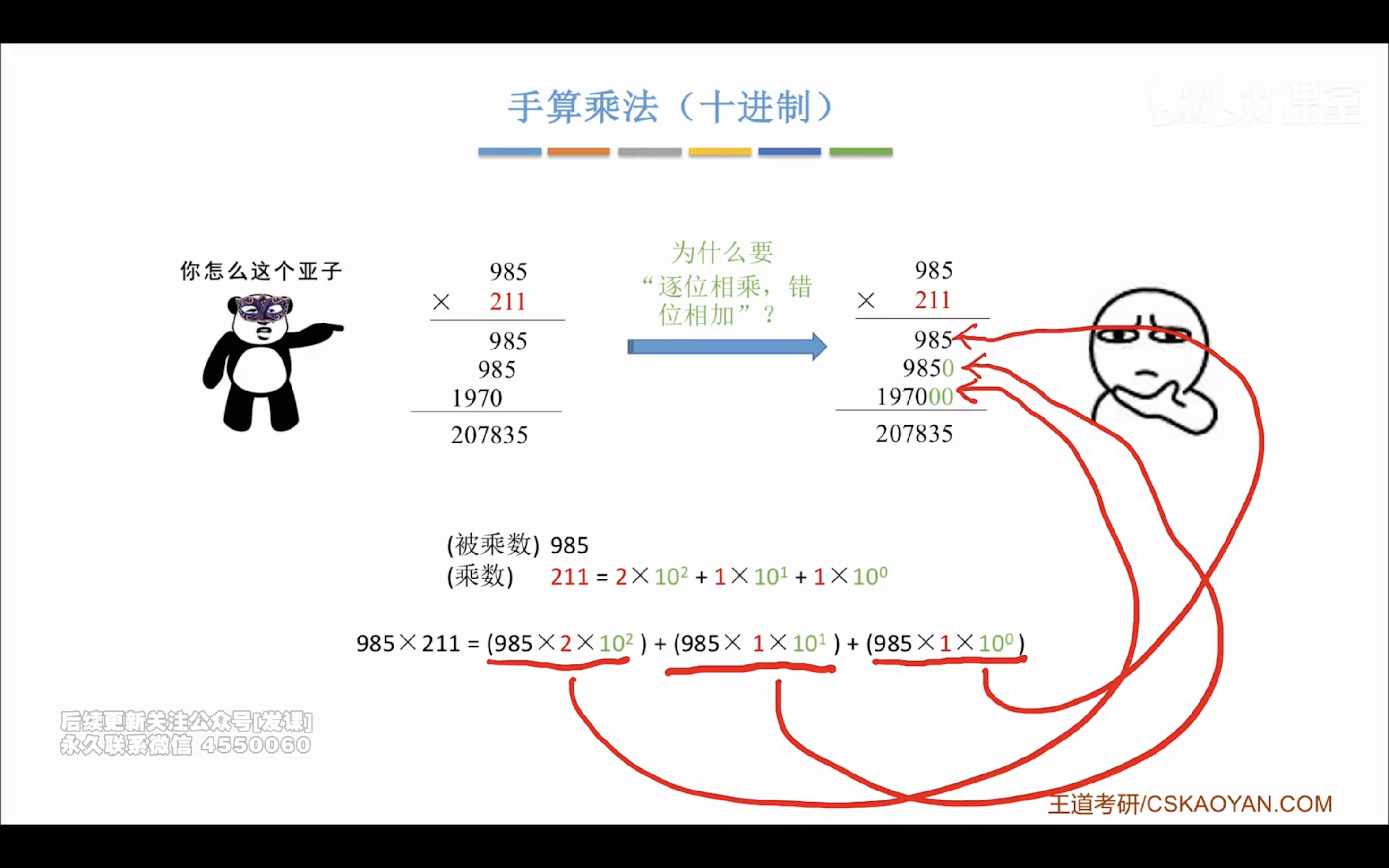
无符号整数乘法
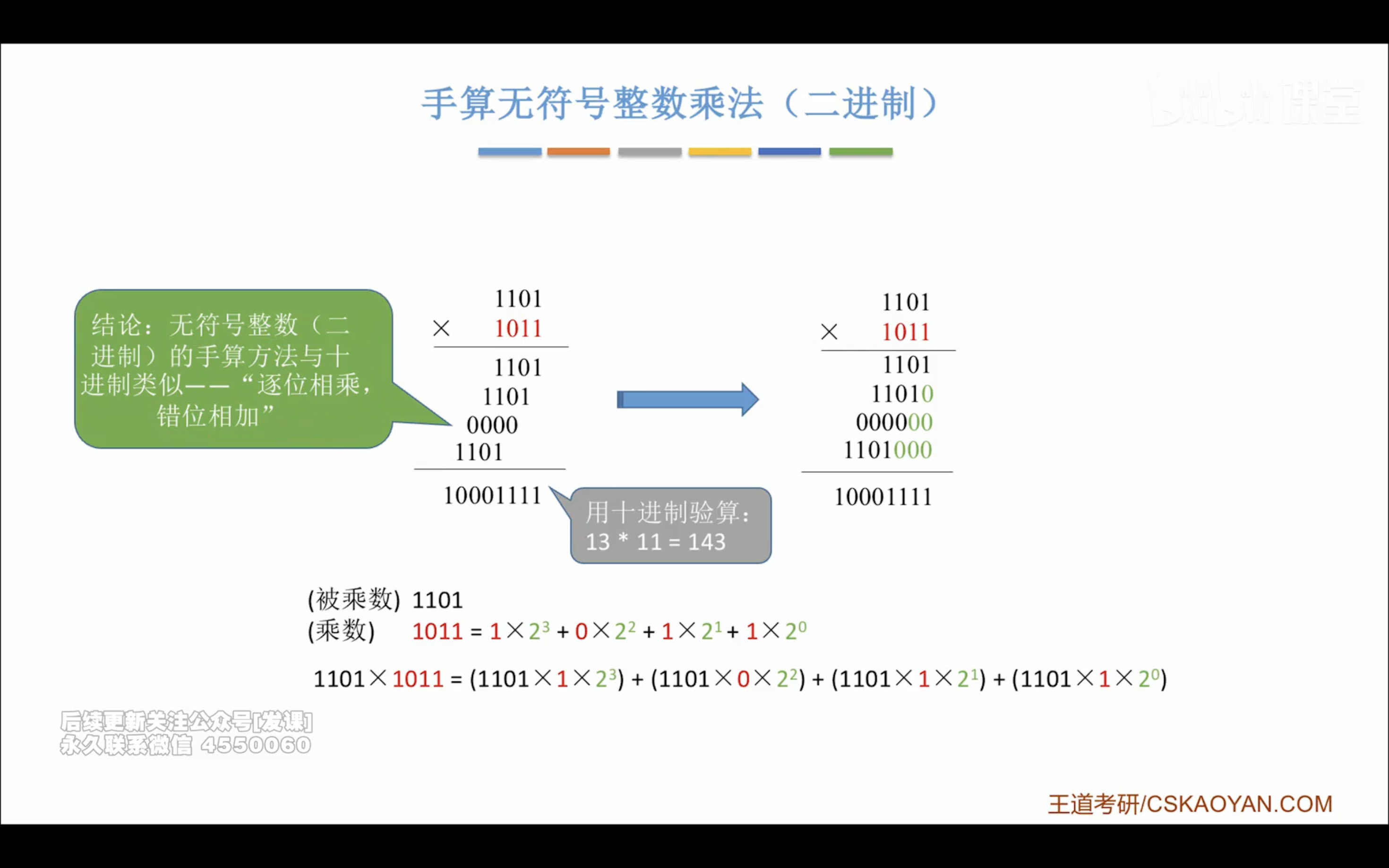
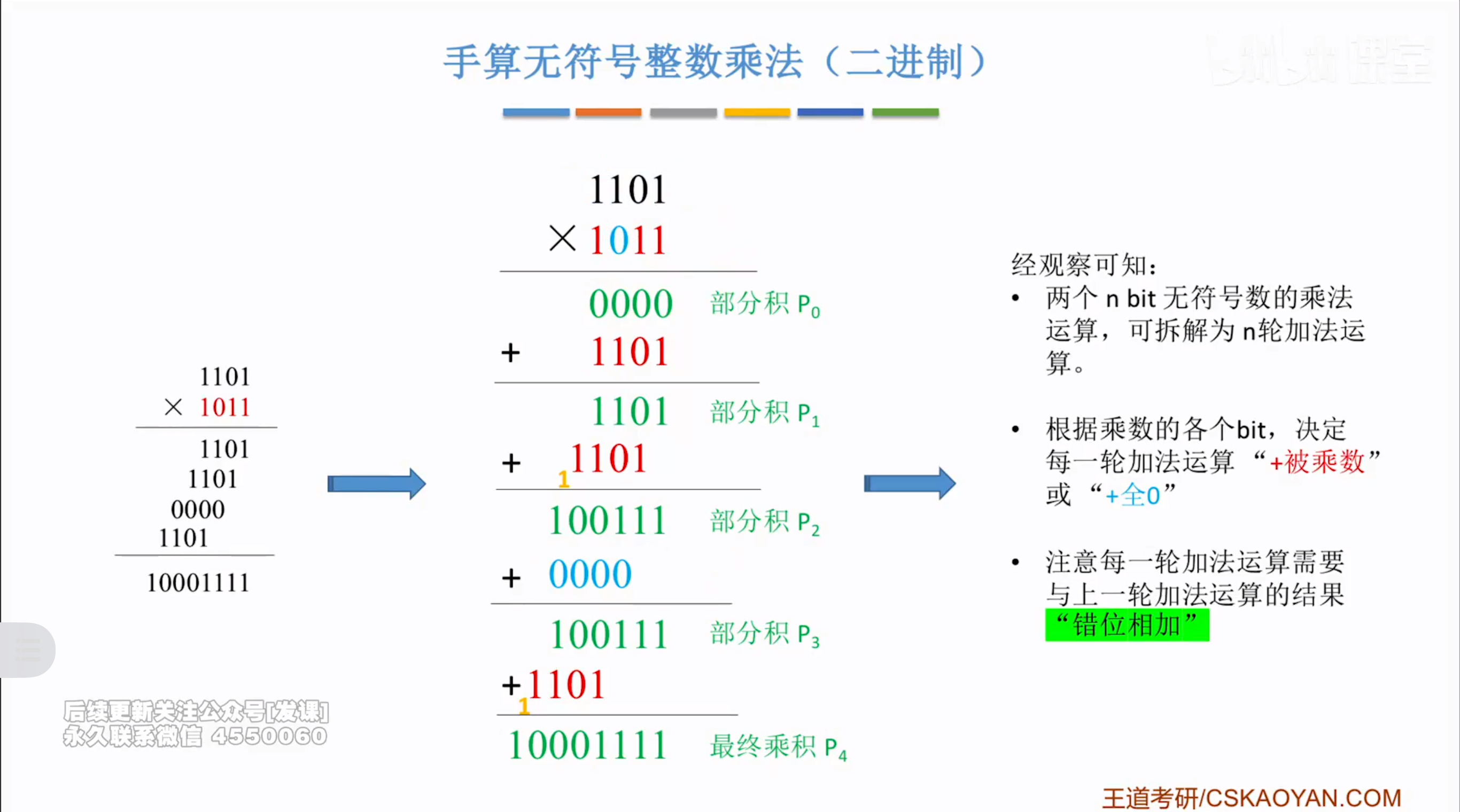
浮点数的表示与运算
浮点数的表示
表示格式
符号、尾数、阶码概念:书p56
符号 +1 -0
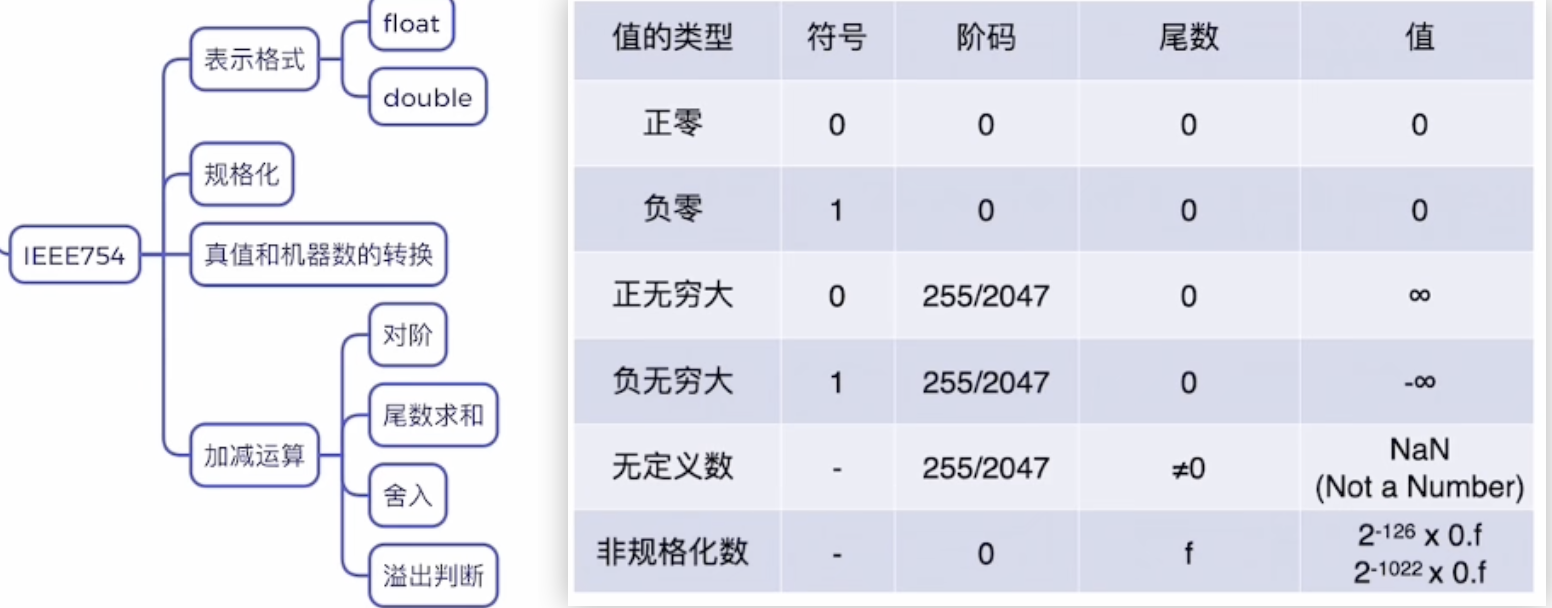
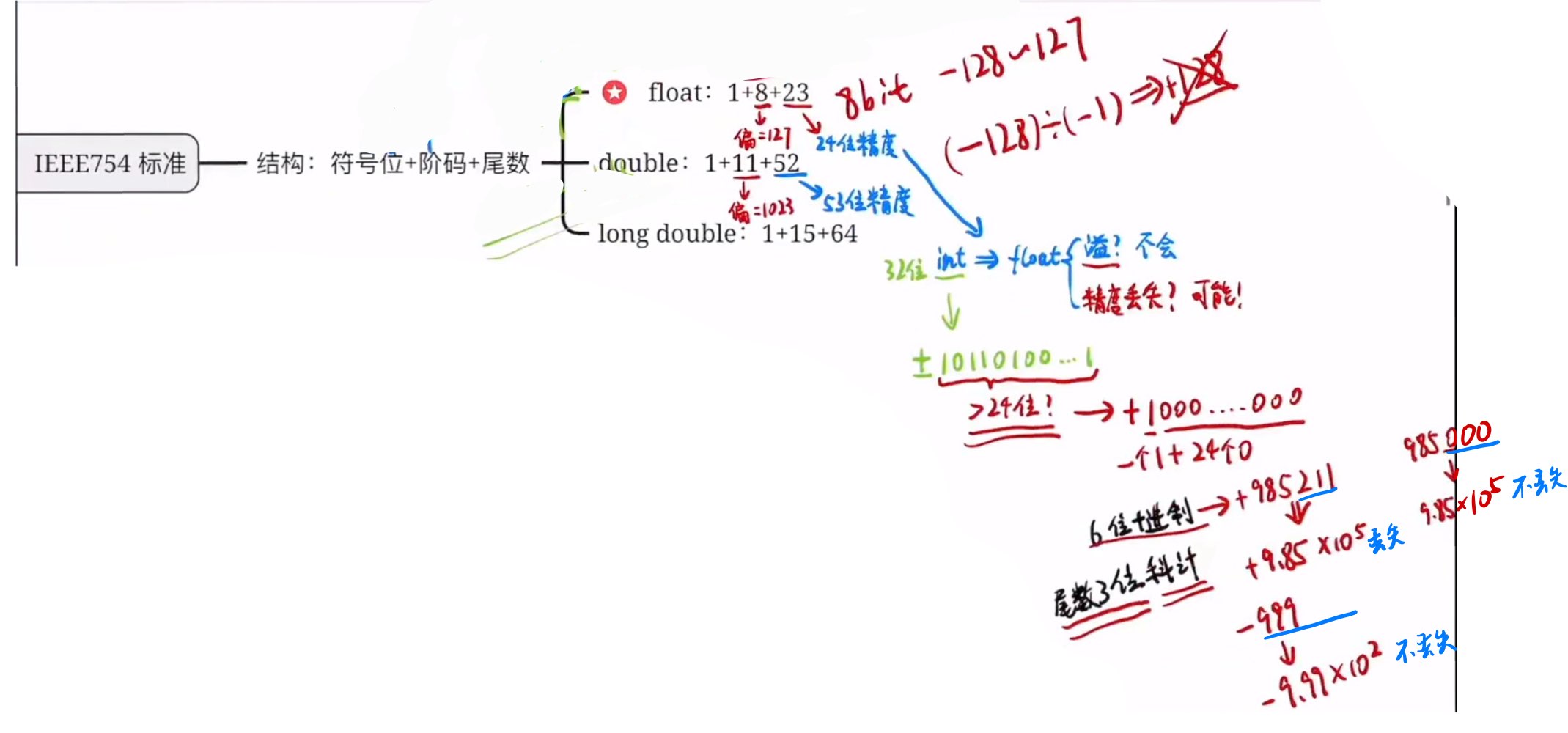
IEEE 754标准
概念什么的见书p57-58划线部分

注意2.中,0.M,M如果是二进制,0.M就是二进制的
例

给浮点数,求机器数
① 整数、小数部分分别转为二进制
② 移 . 小数点改次数,转换为$±(1. xxx)_{2}×2^n$
③ S(1位):+0-1
④ E(8位):次数的真值+偏置值(127)
⑤ M(23位):. 小数点后面的直接抄,不够位数末尾补0

计算真值+127的时候有技巧:算(n-1)+128(n-1+1000 0000)
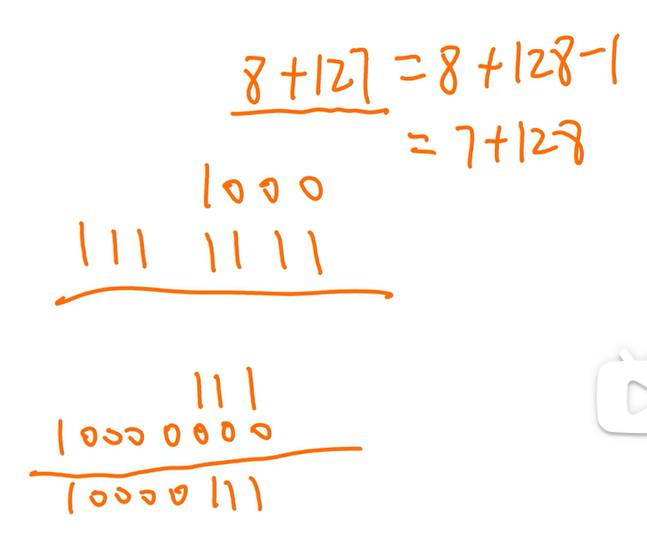
原码的1和小数点不用存,存小数点后面的就行,后面补0
建议写成:___(3) ____(4) _(1),方便后续转成16进制
例

给机器数,求浮点数
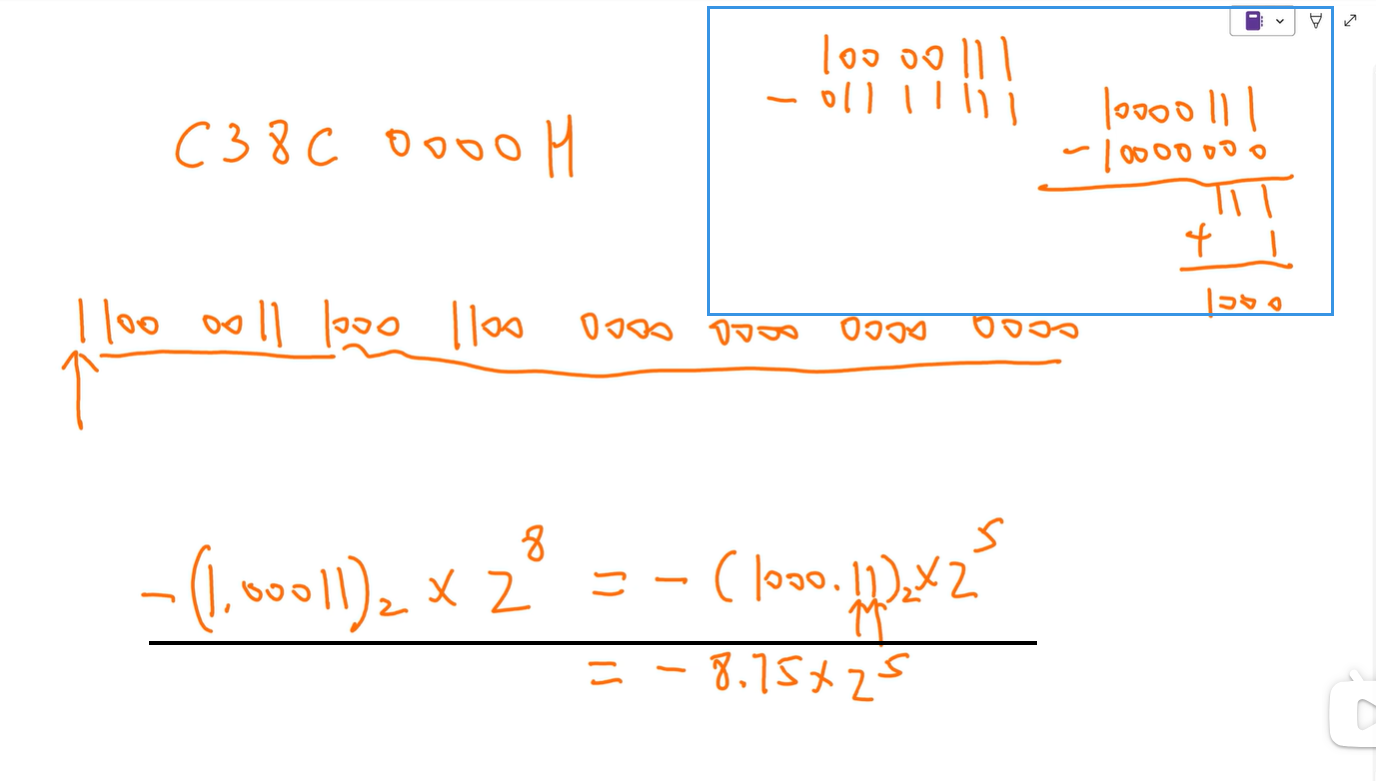
先转二进制
手动添上1.
n-127不好算,技巧:n-128+1(蓝色框框)
最后不好算可以左移小数点3位(黑色下划线)
小结和补充
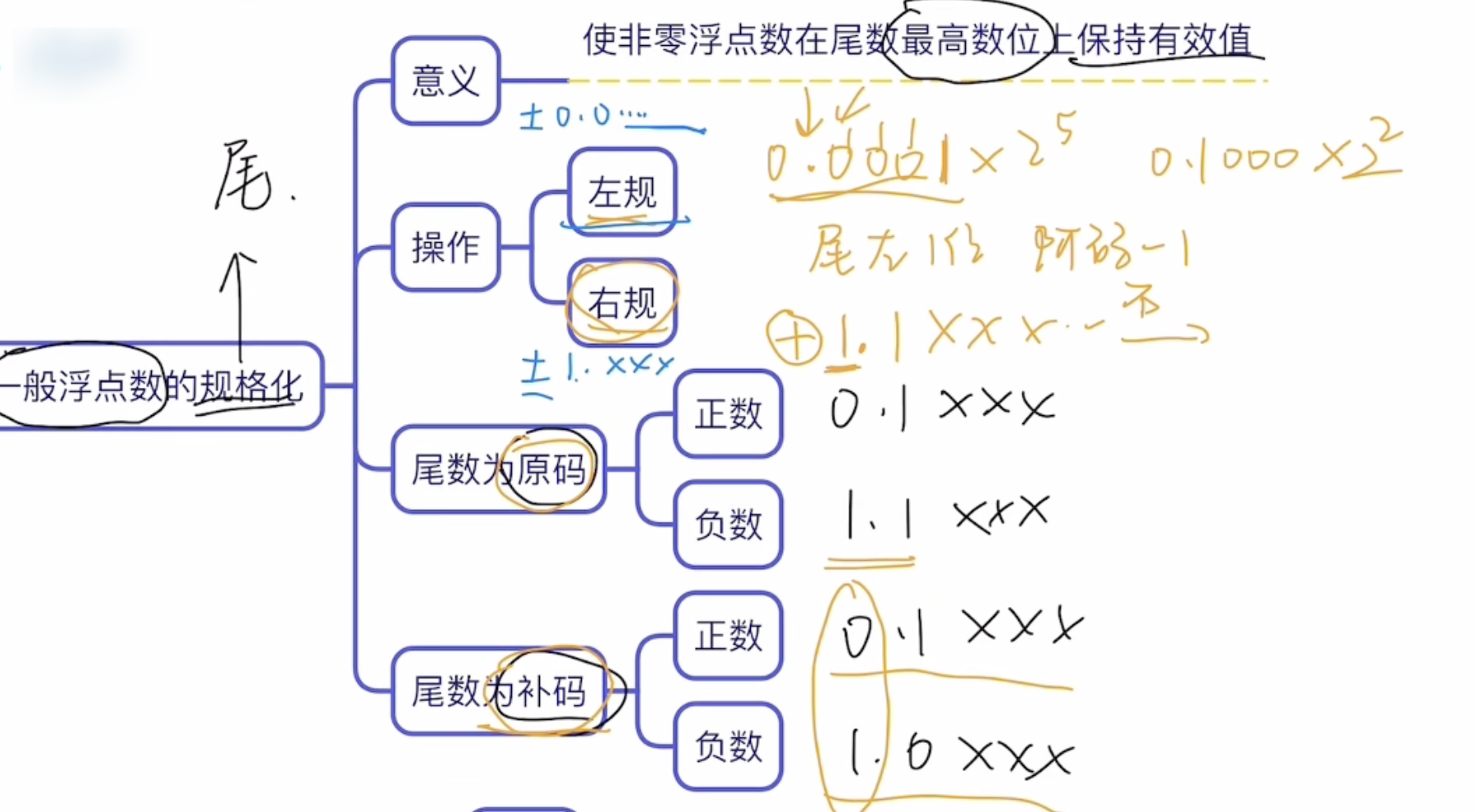
e.g.:
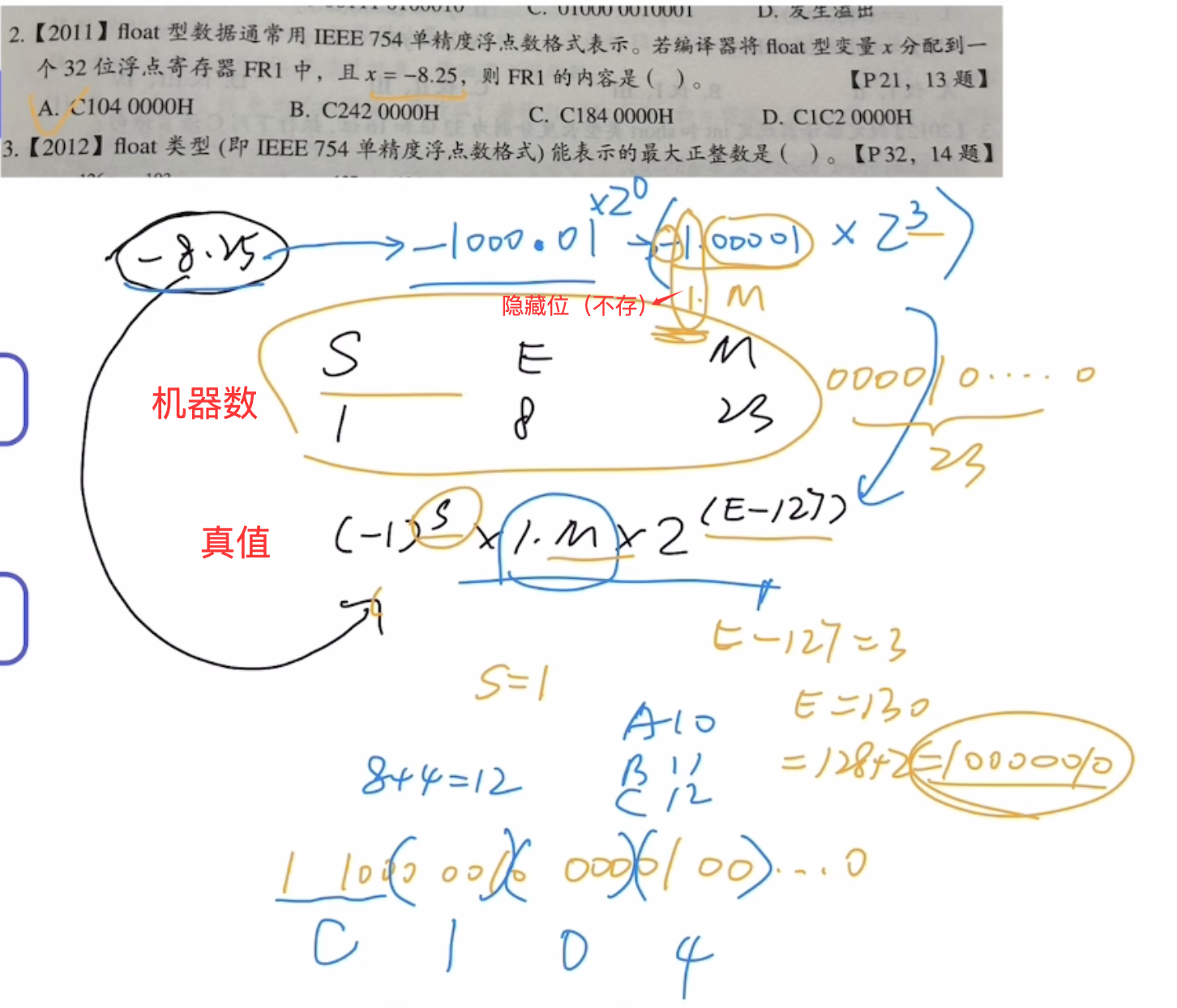
步骤:
1)转化为真值的类科学计数法
2)得到S E M,拼接得到机器数
3)要转换进制就再转换
数据的大小端和对齐存储
占用空间:
int 4B
short 2B
char 1B
书写格式:
0x...、...H:16进制
大小端存储
“边界对齐”方式存储
满足两个要求(见下图)
例

王道强化课
第3章 存储系统
存储器概述
概念看书本p81
主存储器
SRAM和DRAM
DRAM
书p86
行列地址引脚复用:用相同地址线传送行、列地址(分两次传送),地址引脚减半
比如图上传入行号和列号,用2根地址线
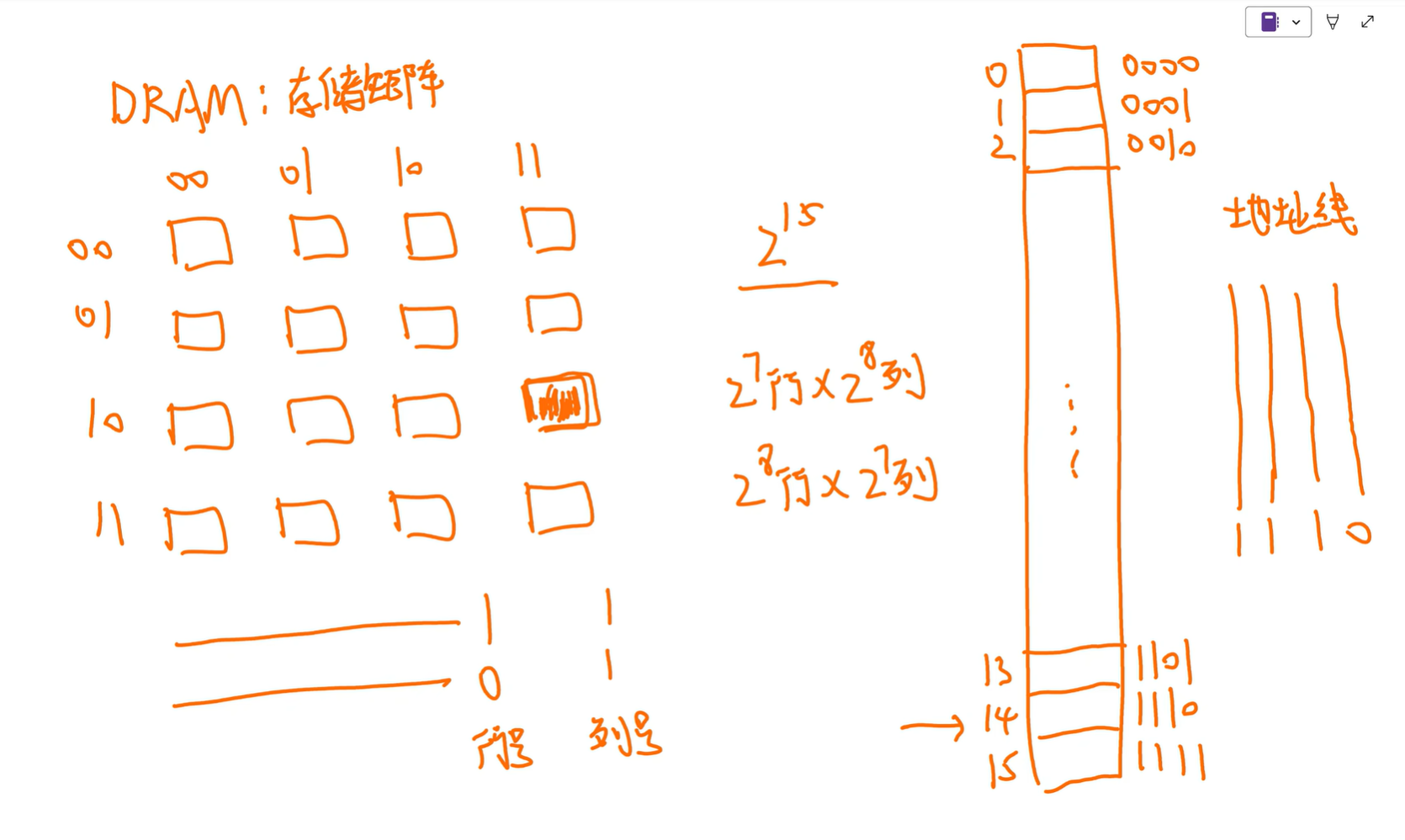
共 $2^{a+b}$ 个存储单元(比如这里是 16)
可以写成 $2^a$ 行 $2^b$ 列(比如这里是 $2^2$行 $2^2$列
地址线数量=max{a, b}
静态RAM(SRAM)和动态RAM(DRAM)区别
书p87
只读存储器ROM
特点、类型:书p88
多模块存储器
单体并行存储器
多体并行存储器
高位交叉编址(顺序方式)
高位是自己芯片(存储体)的编号,低位是自己内部的地址
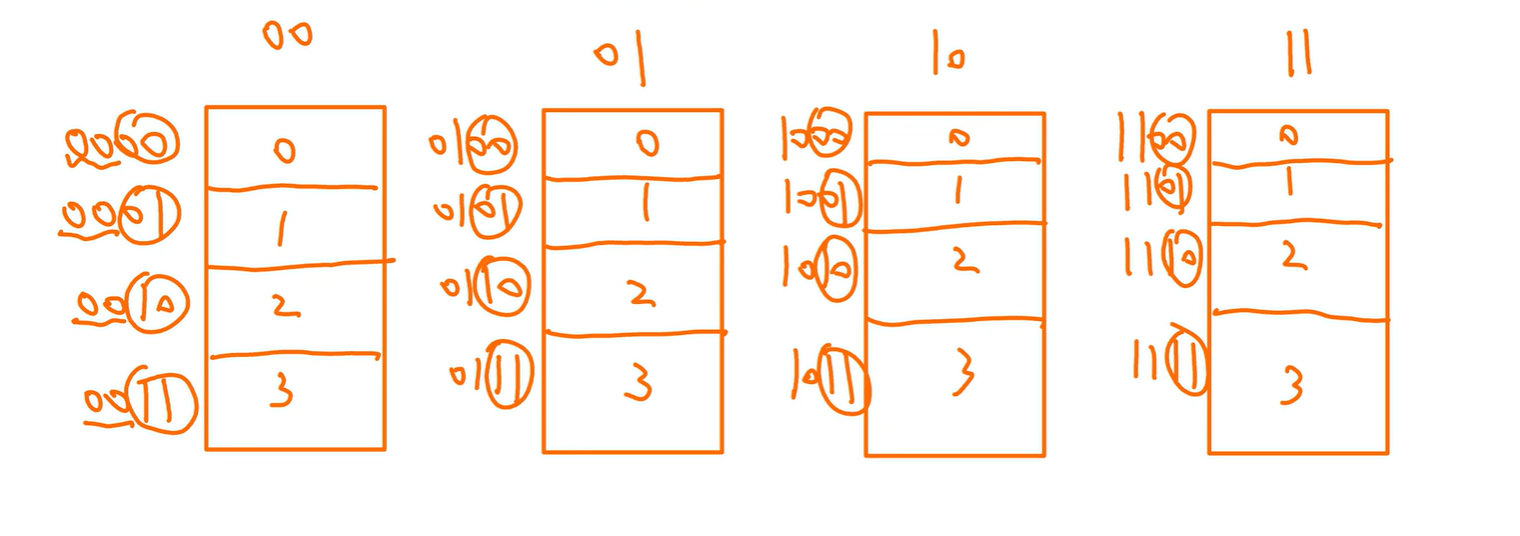
例:

每个存储体1M($2^{20}$),说明低20位表示内部的地址,高3位表示是哪一个存储体
低位交叉编址(交叉方式)(说“交叉编址”默认)
高位是自己内部的地址,低位是自己存储体的编号
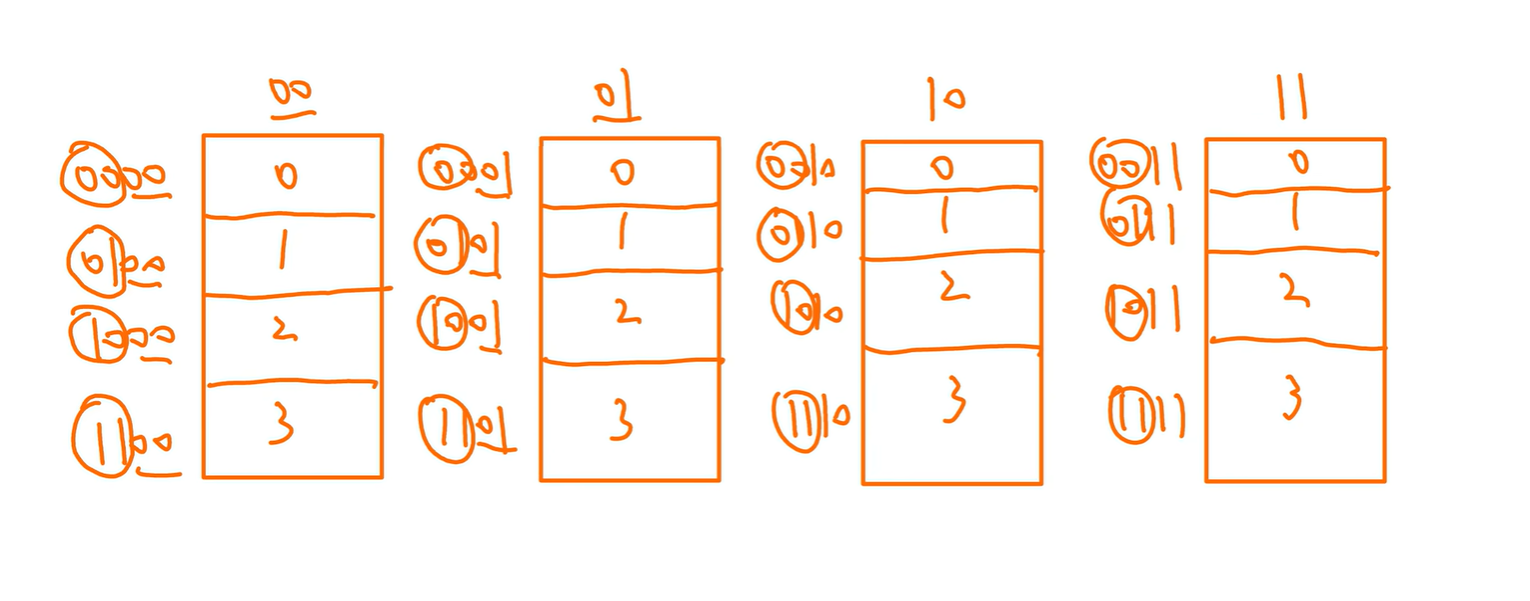
例:
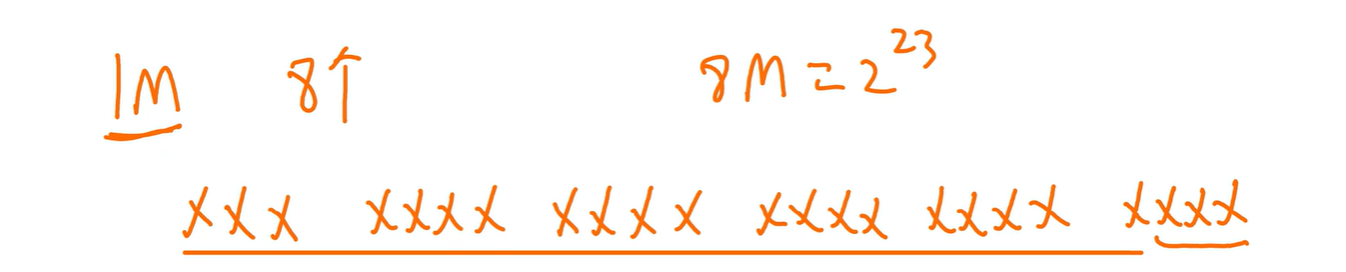
每个存储体1M($2^{20}$),说明高20位表示内部的地址,低3位表示是哪一个存储体
交叉存储器可采用轮流启动或同时启动两种方式
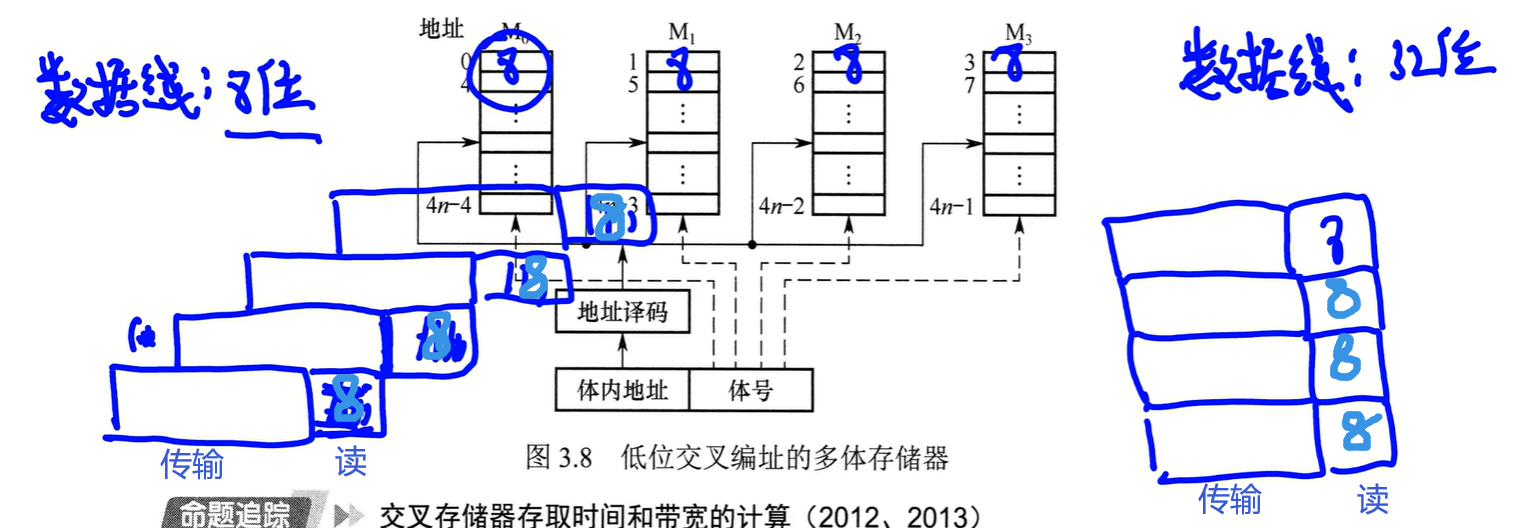
判断是哪种方式只需要看数据线是=单个模块数or汇总数
扩展了解
高位划掉,对于每个存储体只有4个地址,2位即可表示
拿到4位地址后,通过高两位锁定某个存储体后,只要看低两位就行
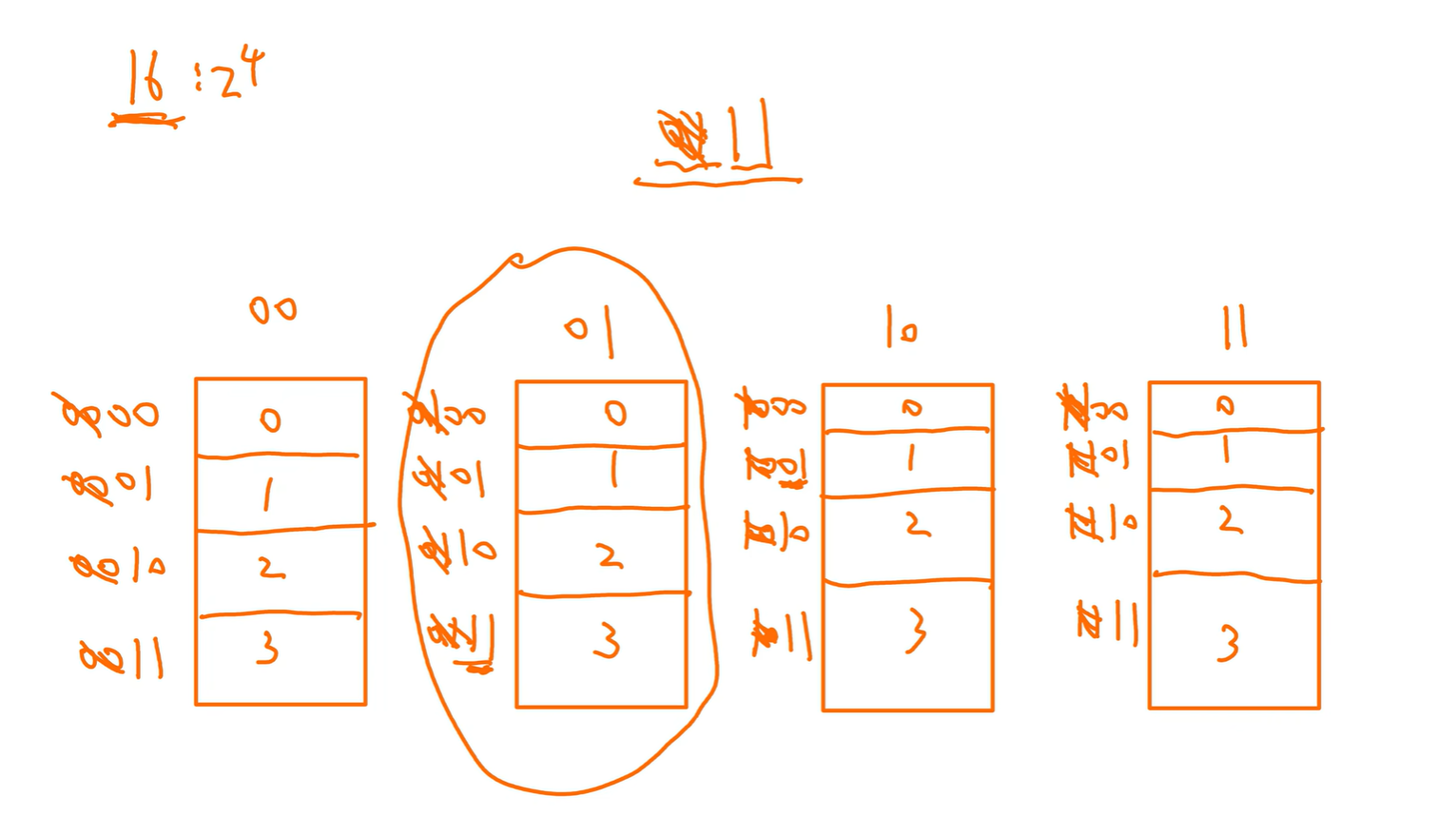
本节例题
30.

地址引脚:地址线(这里11)
数据引脚:数据线(这里8)
答:A.
33.
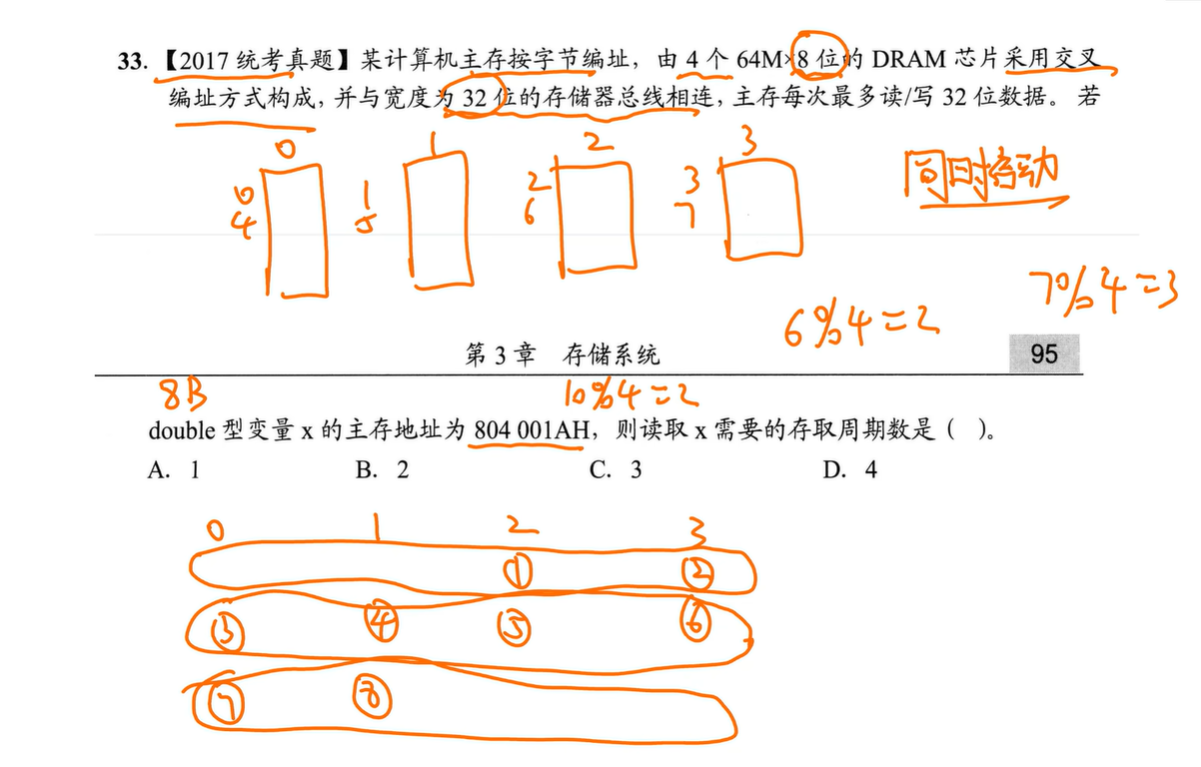
宽度为32位的存储器总线(也就是数据线)
4个64M×8位=>每个地址内容8位
=>4个加起来32位
=>同时启动
交叉编址:判断每个地址在哪个模块,用地址对模块总数(这里是4)取余即可
如图中的例子:6、7,分别在2、3模块
10%=4,x从2开始
double占8字节Byte(64位),每个模块8位bit
同时启动,一次能读所有模块相同的地址,拼到一起变成32位(4模块*8位(2bit4*4)*)
共占3行=>3个存储周期
答:C.
主存储器与CPU的连接
位扩展:地址不变,每个地址能放的位数变多了(变宽)
8个芯片取出的地址一样,数据汇总到一起
CPU数据线数>存储芯片数据位数
字扩展:总地址(即存储字长,每个单元叫一个存储字长)变多(变长)
CPU数据线位数=芯片数据线位数,CPU地址线位数>芯片地址线位数
字位同时扩展
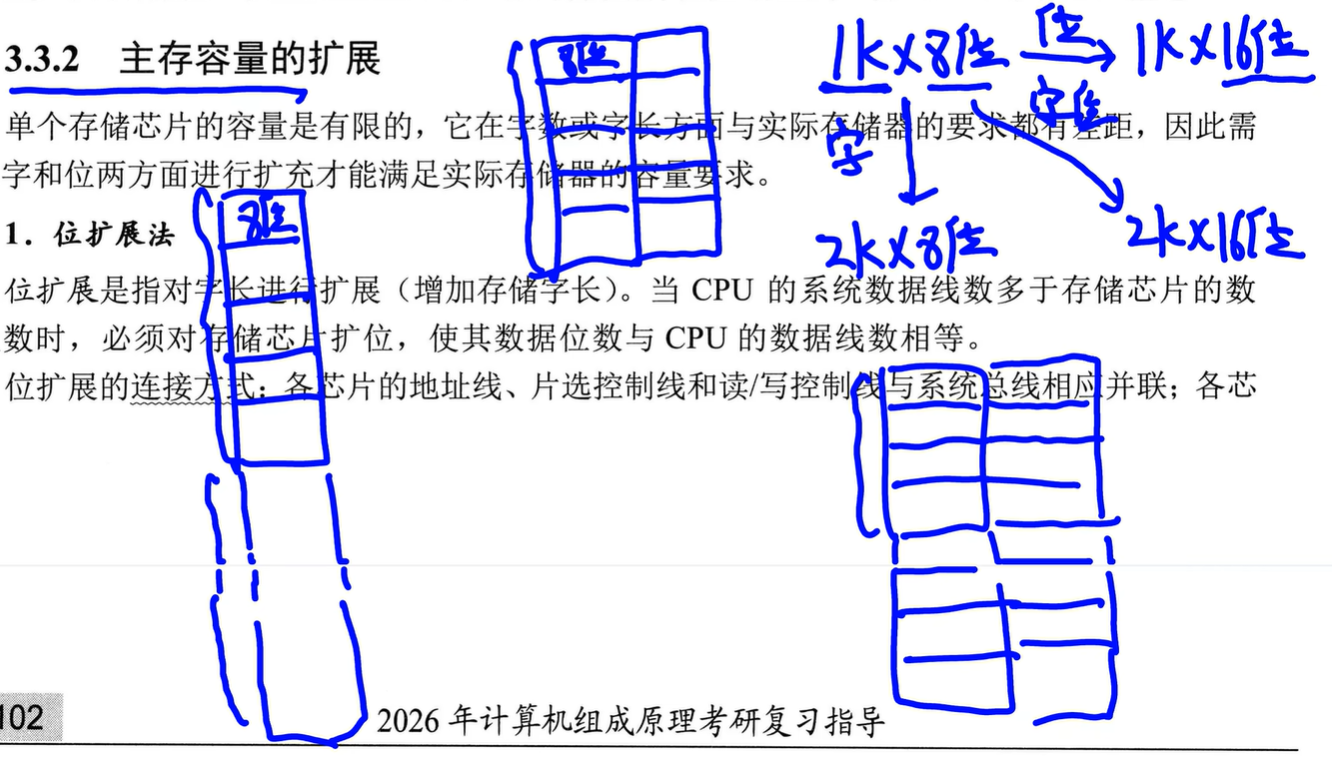
示意图
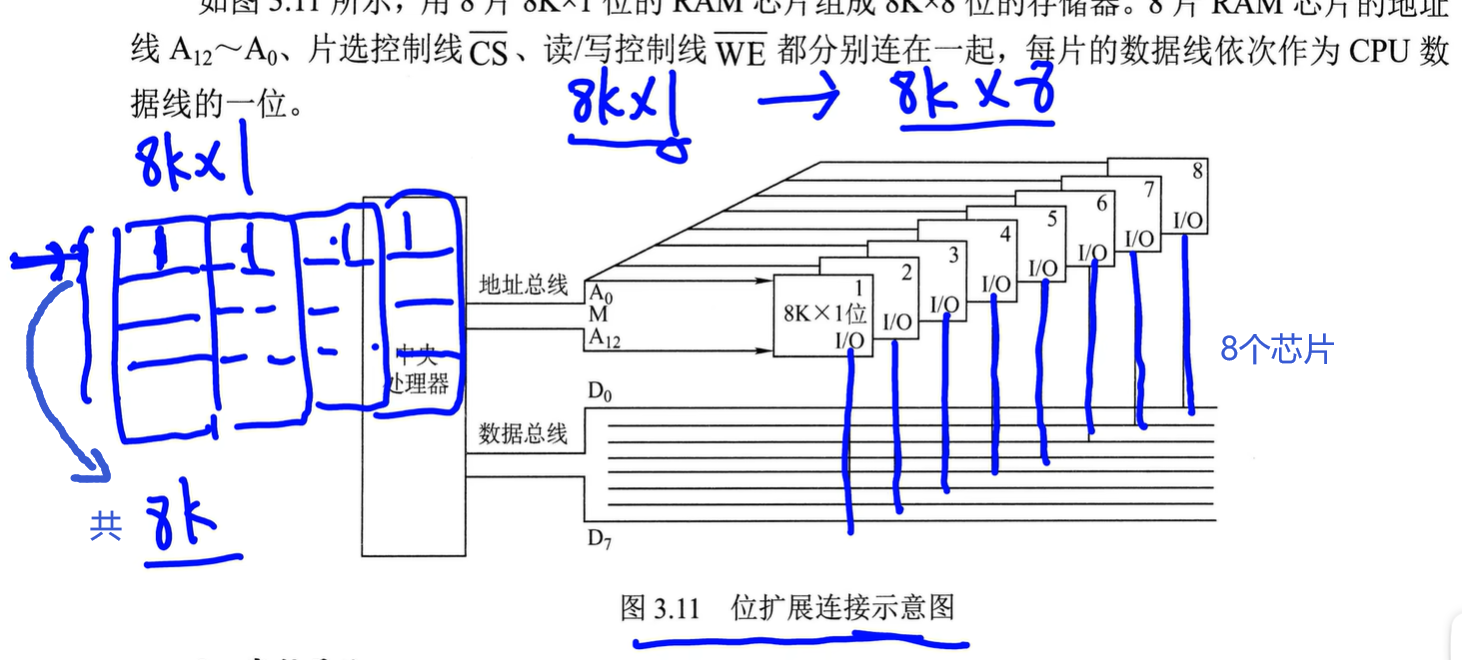
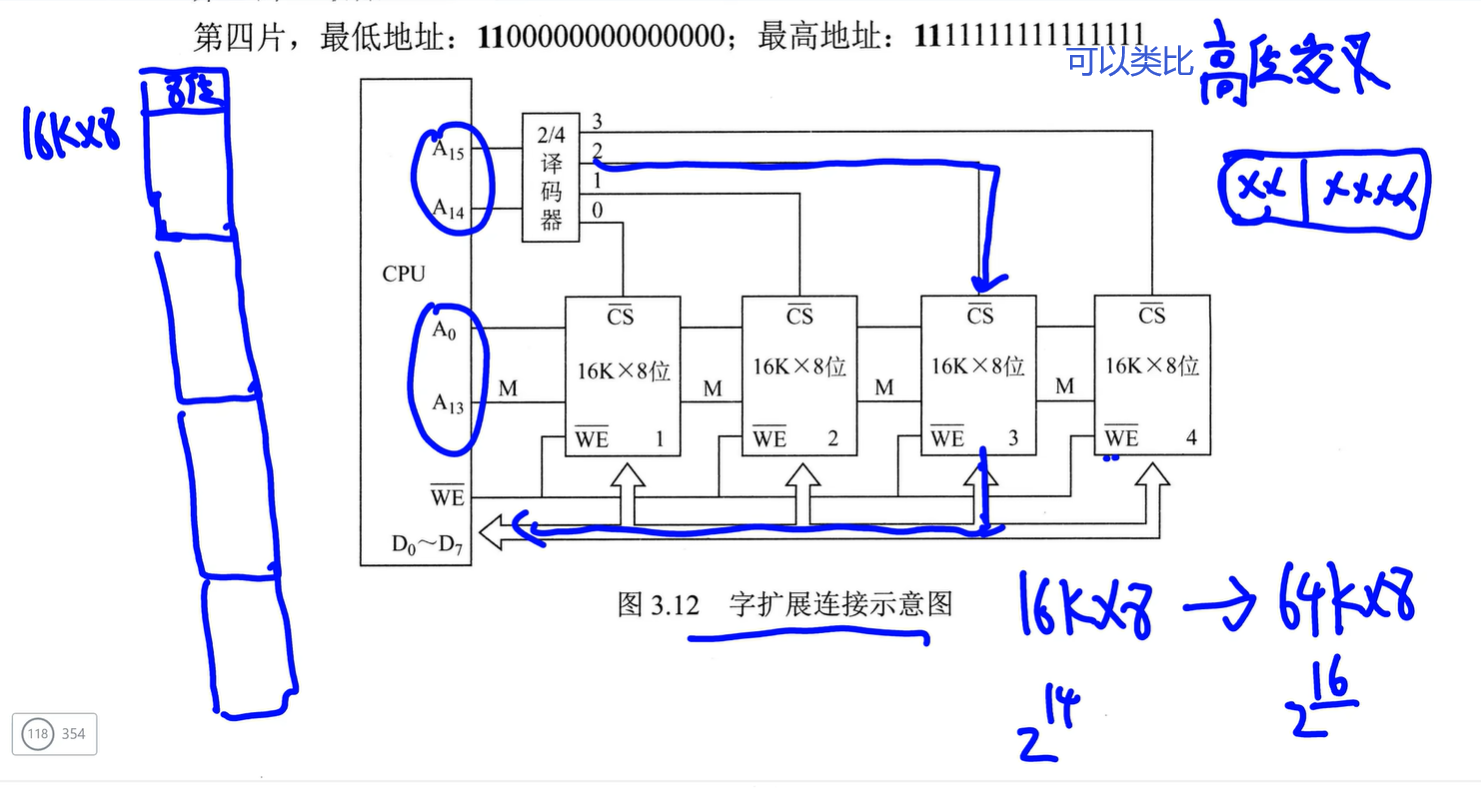
14根地址线,但CPU传16位地址,高2位是芯片编号,经过译码器翻译到对应的芯片(模块),芯片内具体位置只用低14找即可
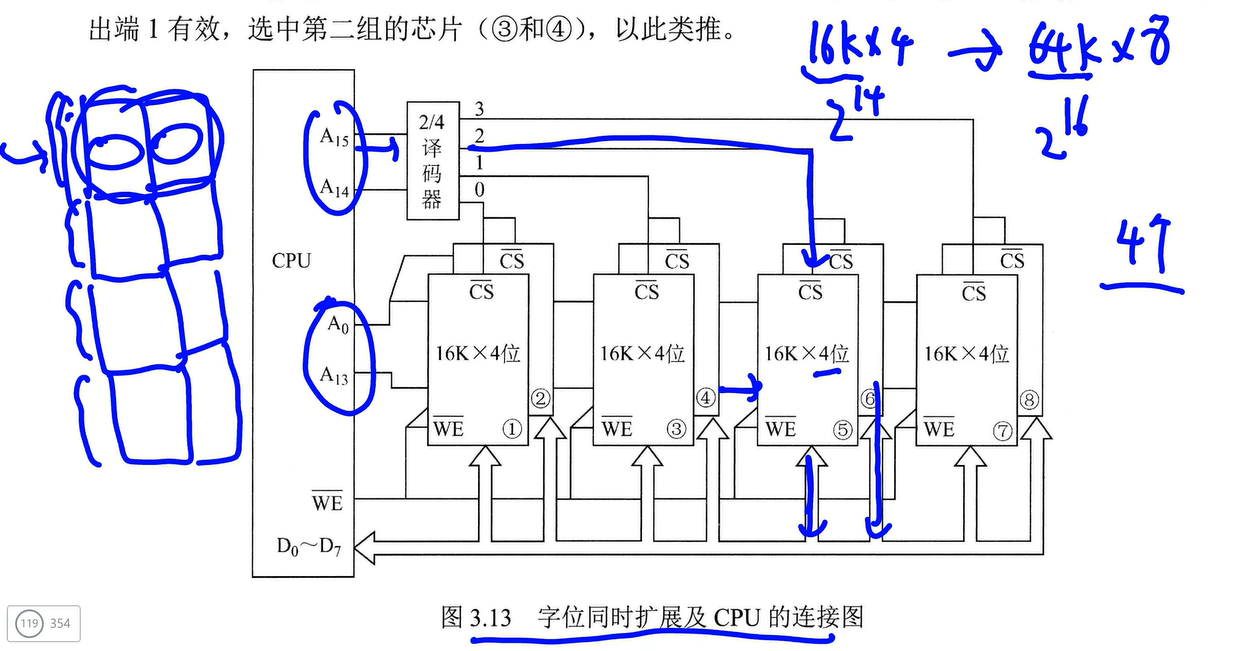
本节习题
15.

4000H~5FFFH 有2000H=$2×16^3$(8K)个地址
按字节编址=>1个地址1字节=>8K×8位
=>ROM 8KB
共64KB=>RAM 56KB=56K×8位
8K->56K:×7组
4位->8位:×2
=>14个芯片
外部存储器
高速缓冲存储器 Cache
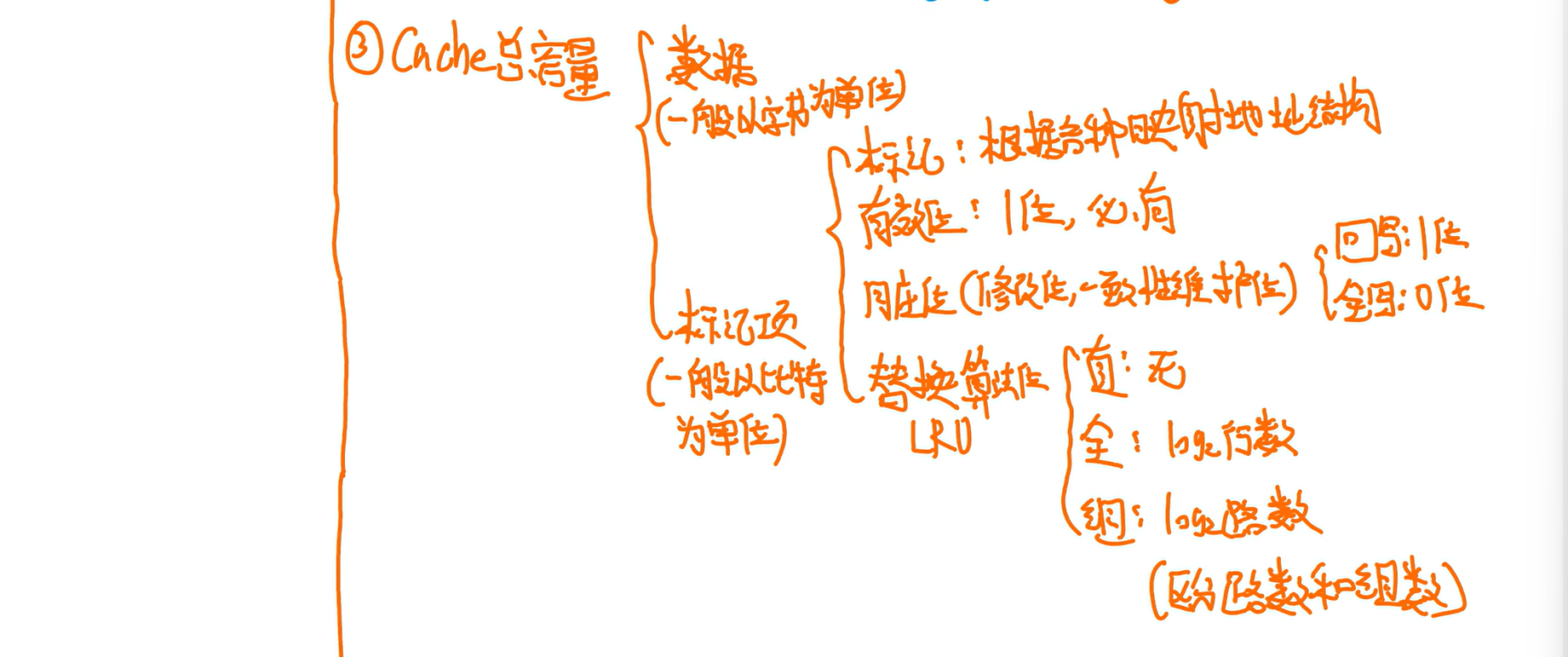
Cache总容量 = 行数×每行容量(内含数据和标记)
Cache 和主存的映射方式
时间局部性:访问过的数据可能再一次访问;空间局部性:访问过的数据的邻近空间可能被访问
直接映射
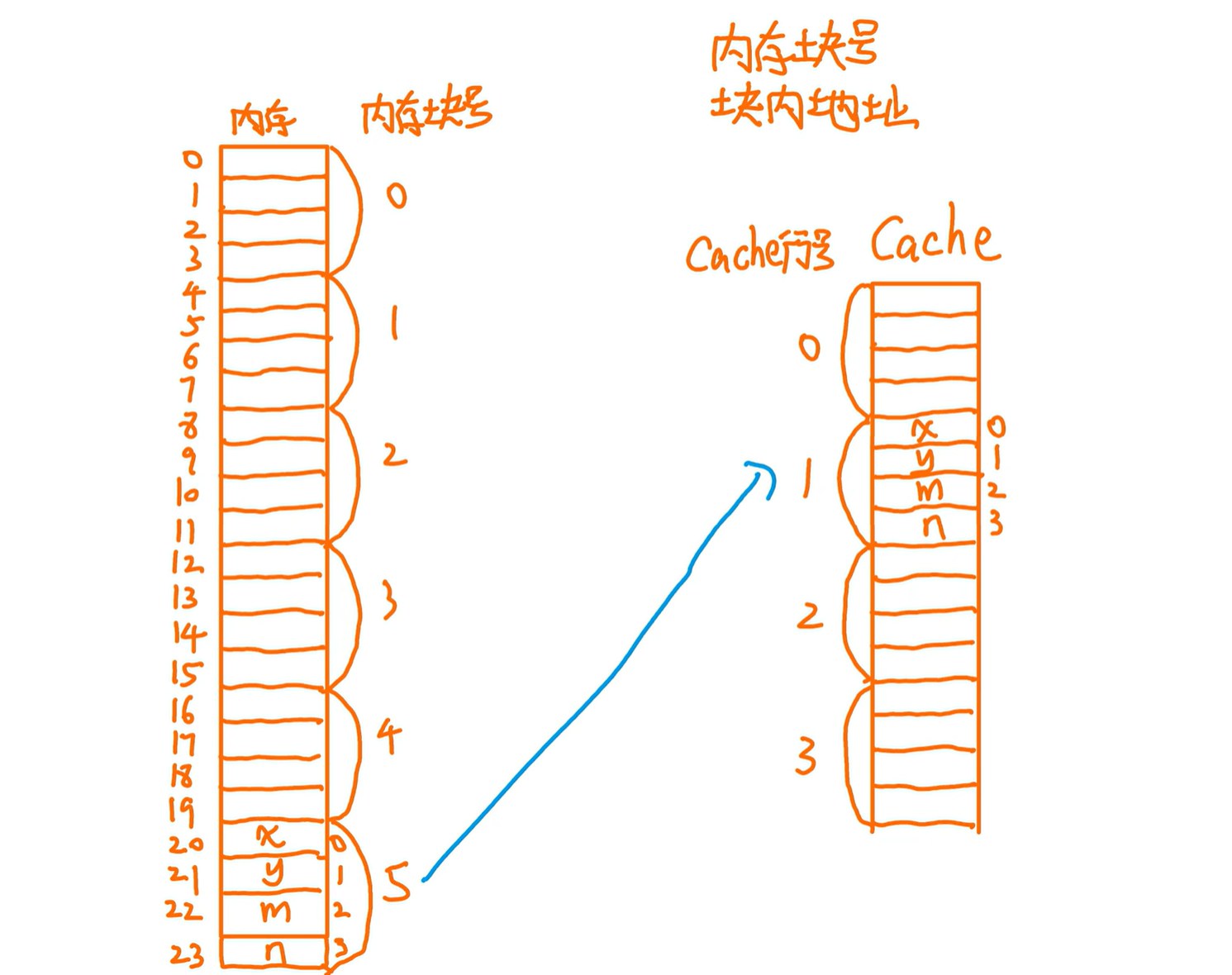
已知内存地址,计算块内地址(下下图上左边)
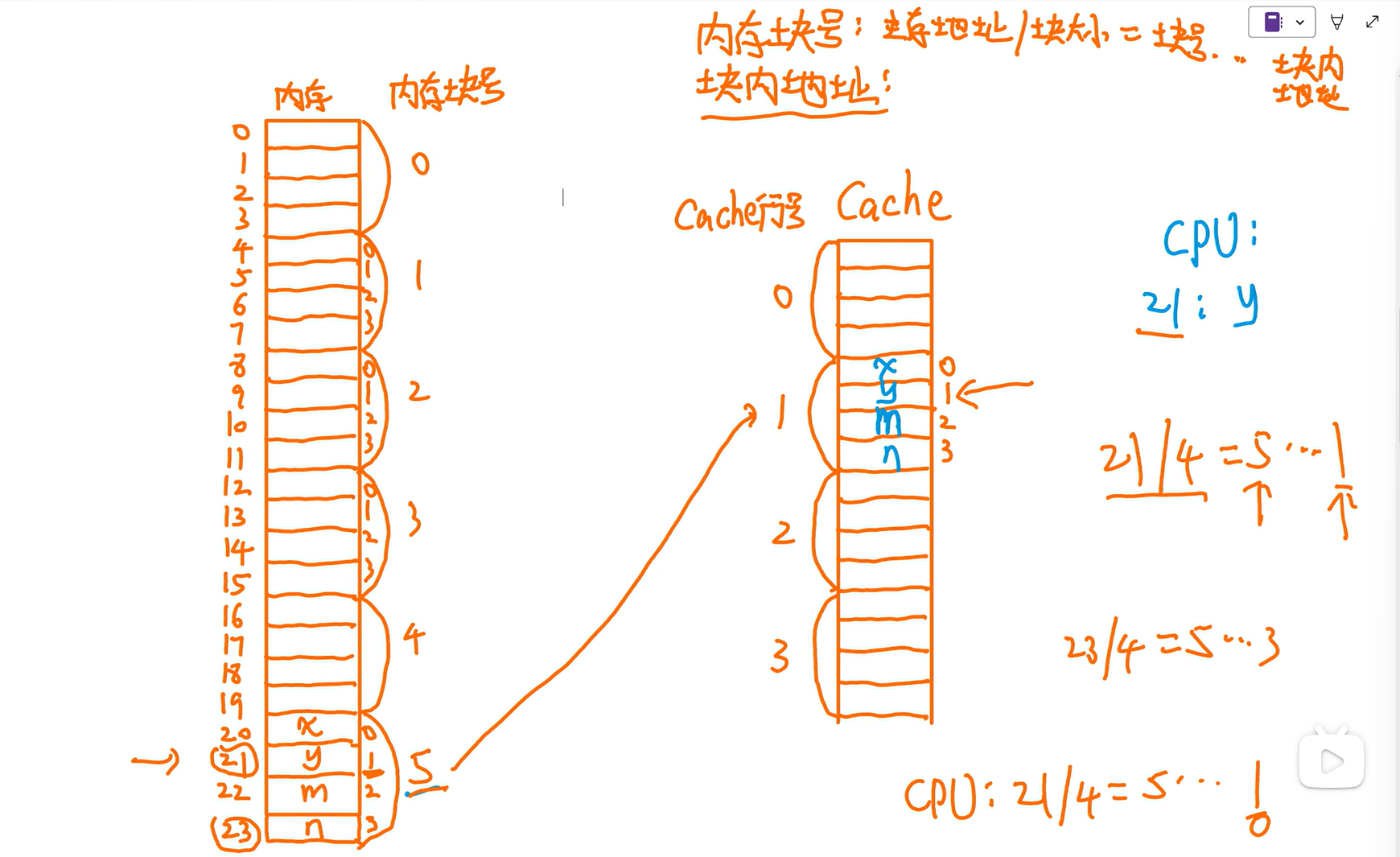
已知内存块号,计算Cache行号(也就是块号)(下图上右边和左边下方)
看标记判断放的是是哪个内存块的
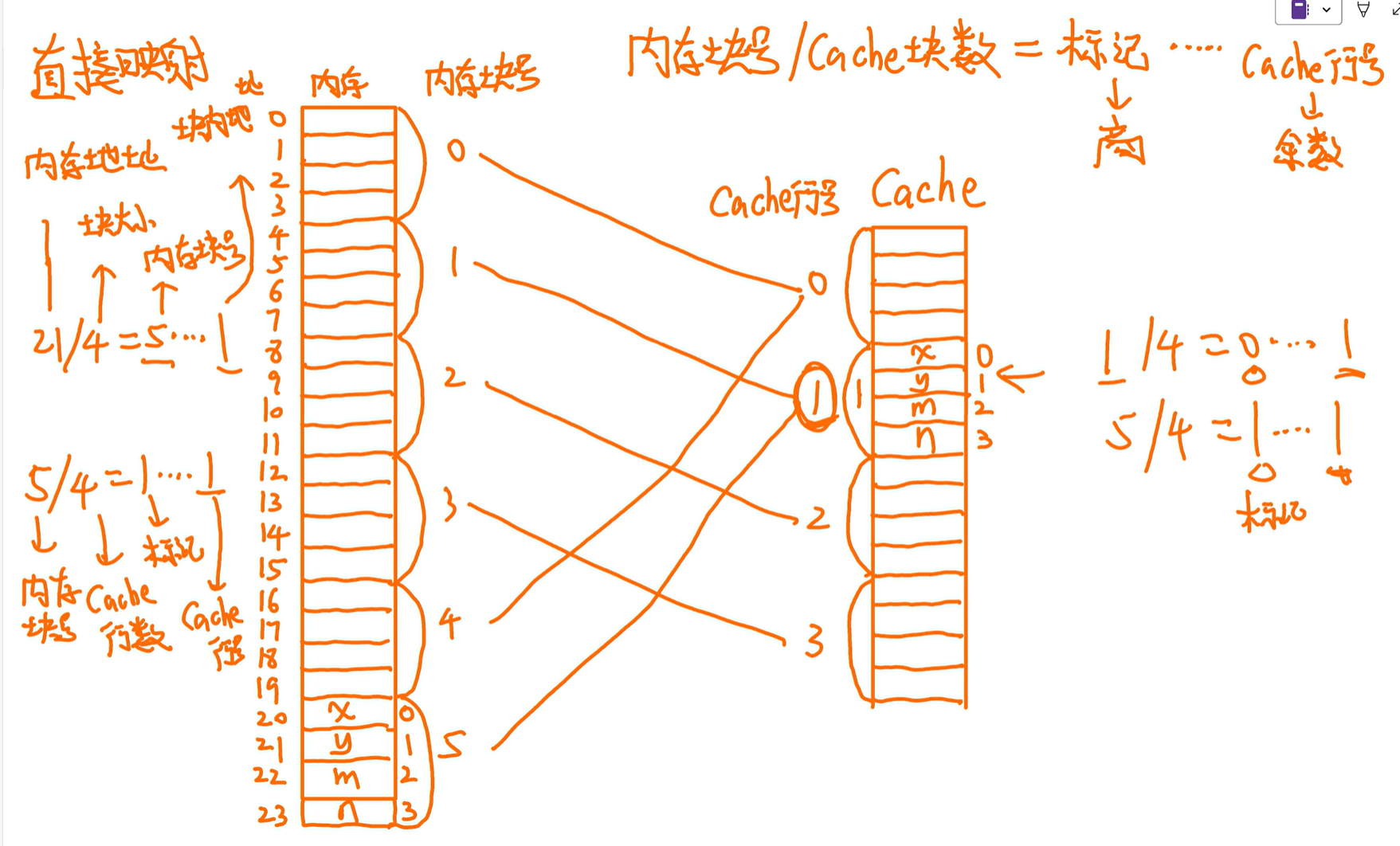
CPU找21:
内存:21
Cache:1行块内地址1
上面是十进制表示地址,二进制表示也一样
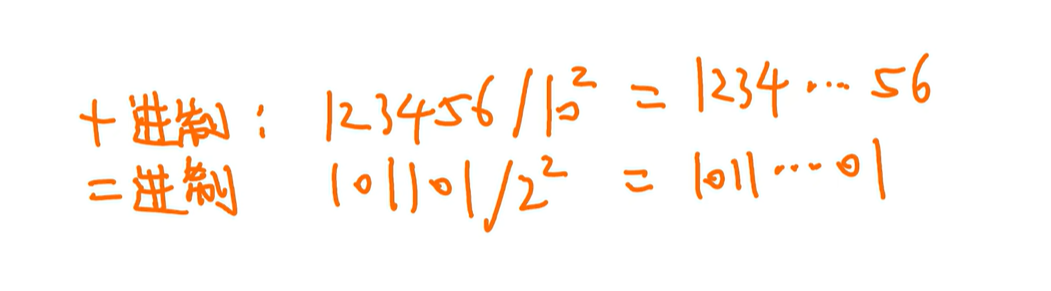
就图上这样取余
例:
CPU找21(0001 0101):直接拆分就行
(21/4) 0001 0101/$2^2$
=>低位 01 表示块内地址,高位 0001 01 表示块号
0001 01/$2^2$
=>低2位表示余数,是块内内地址,高位是标记
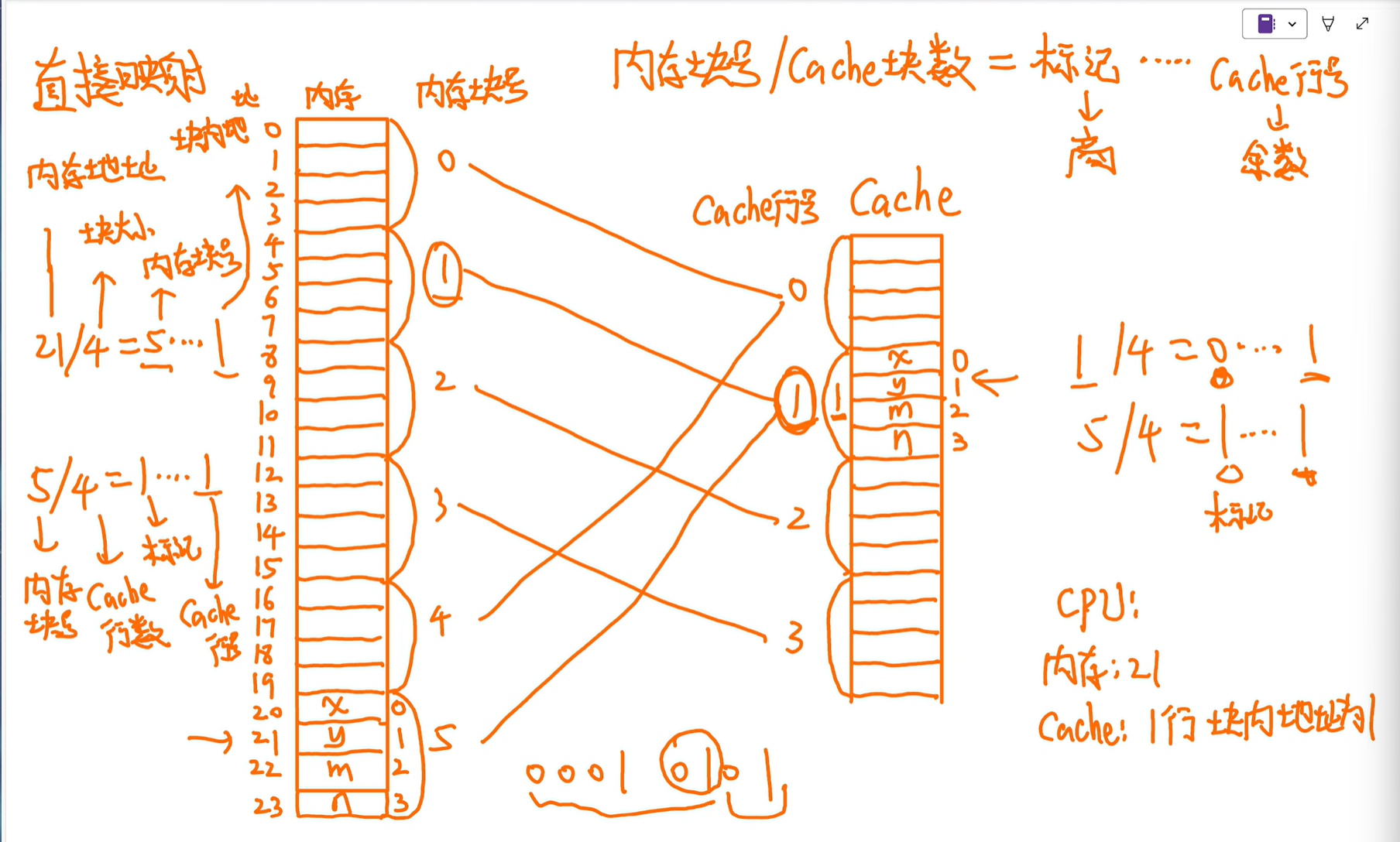
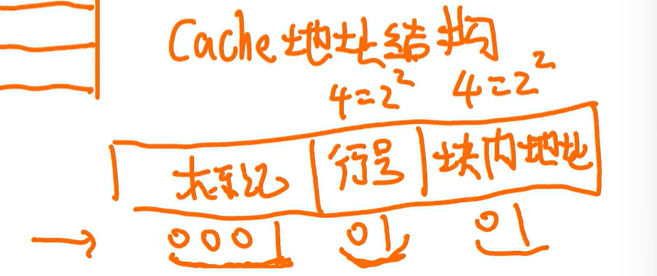
全相联映射
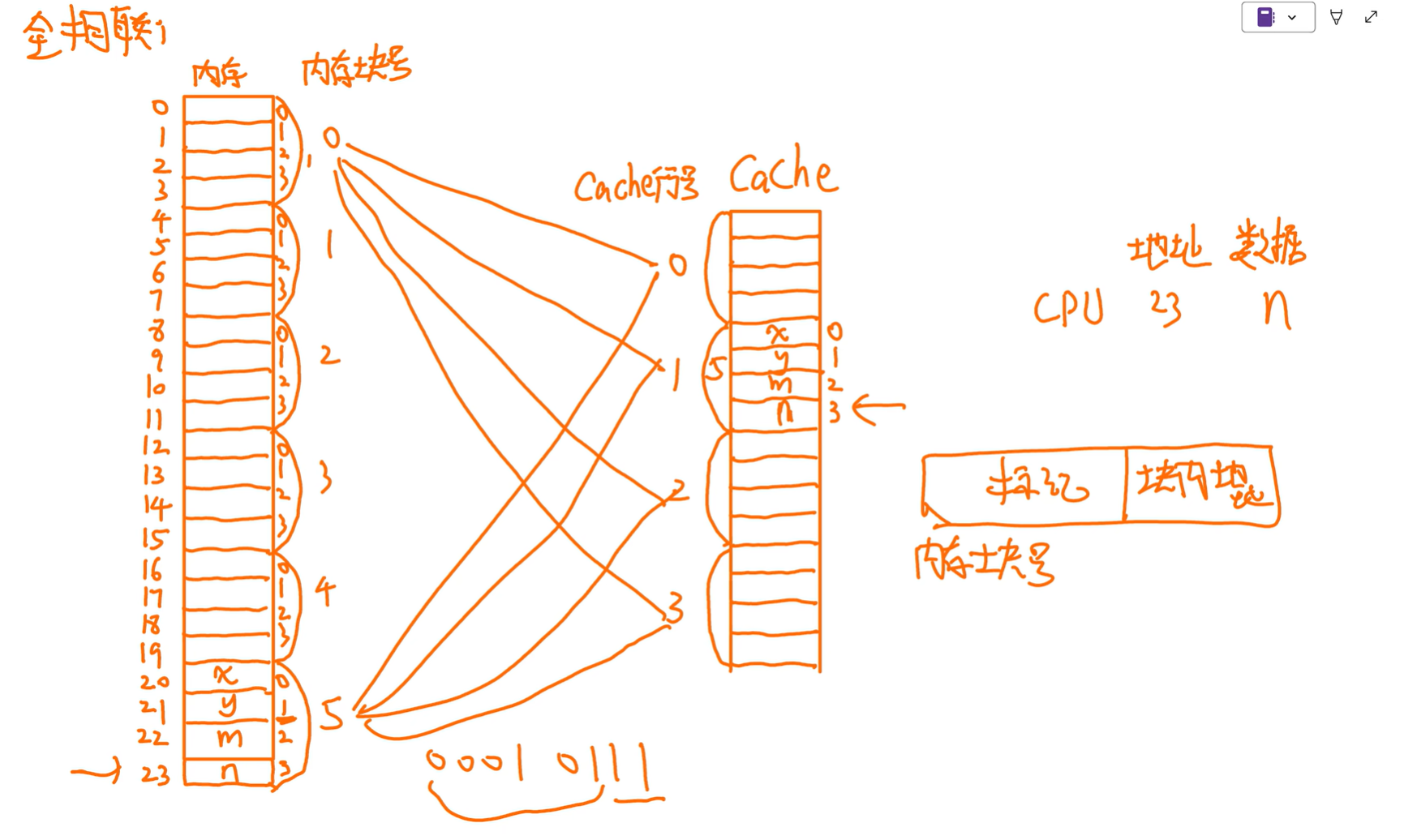
内存块号作为标记,记录放的是哪一块
组相连
cache分组
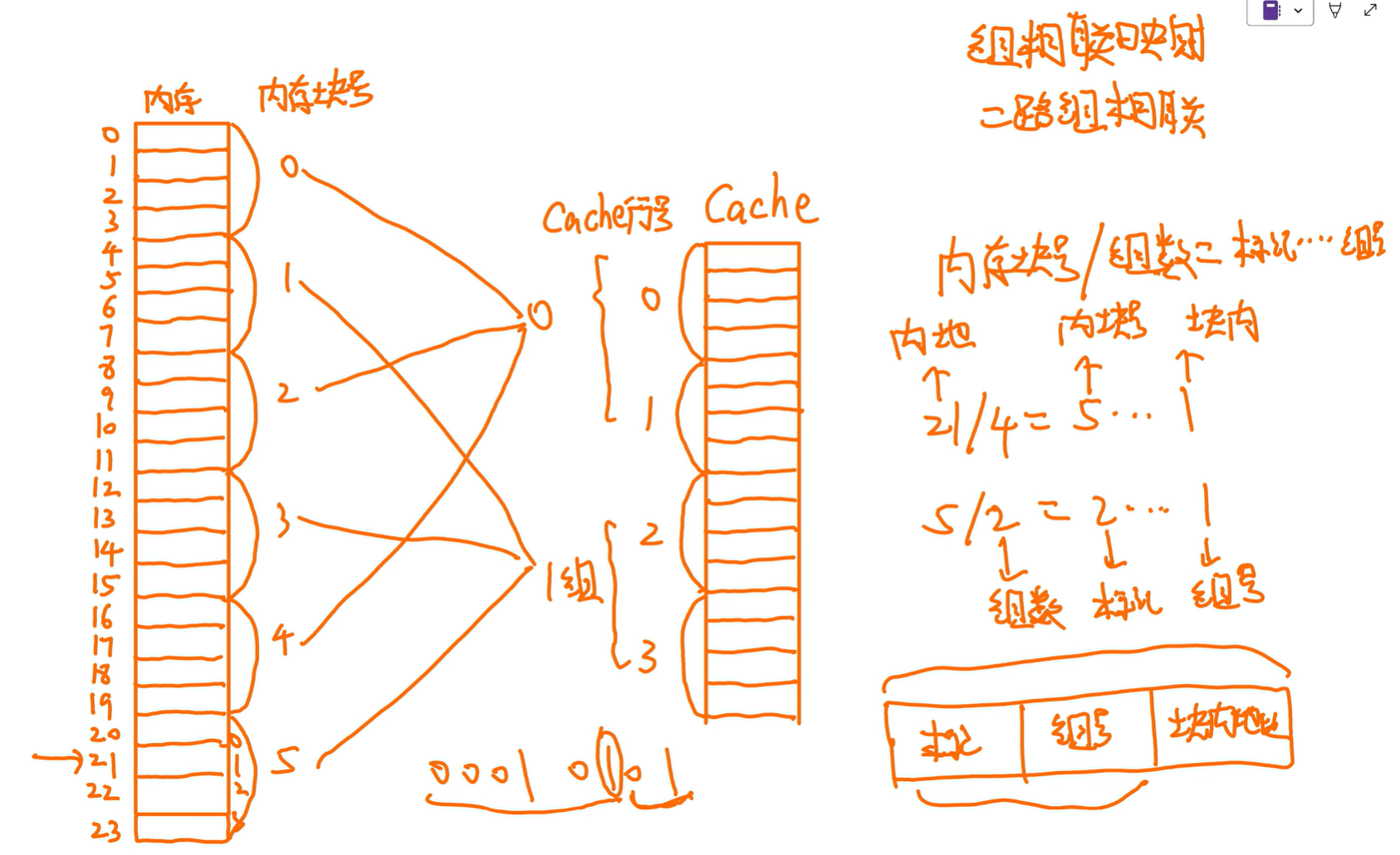
具体放到这组哪个位置随便放,组间直接映射,组内全相联
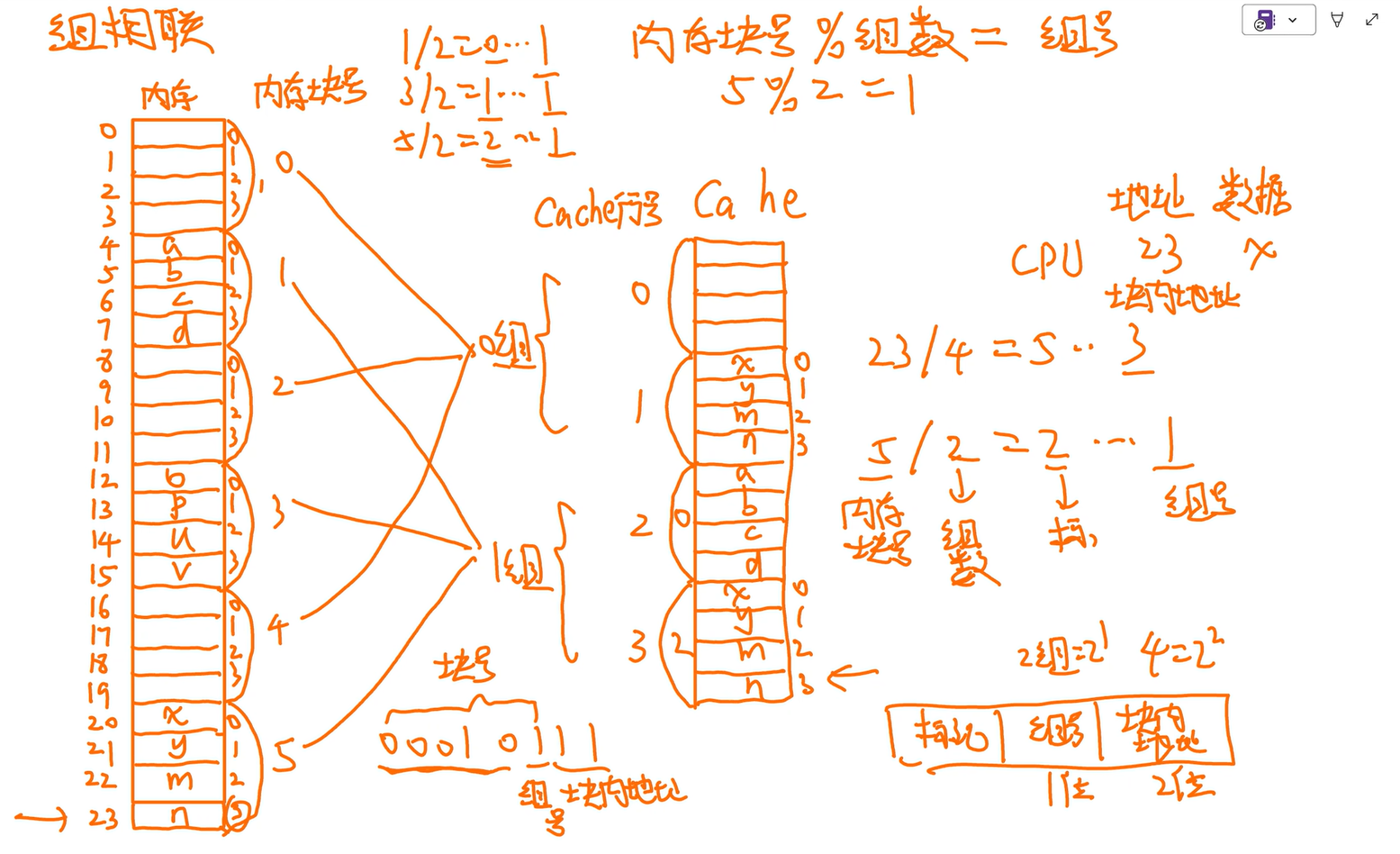
Cache 中主存块替换算法
LRU
最久未使用 LRU(Least Recently Used, 近期最少使用)算法(记忆:Longest Remaining Unused)
计数值的位数:$log_2路数$
Cache 的一致性问题
p123
总结
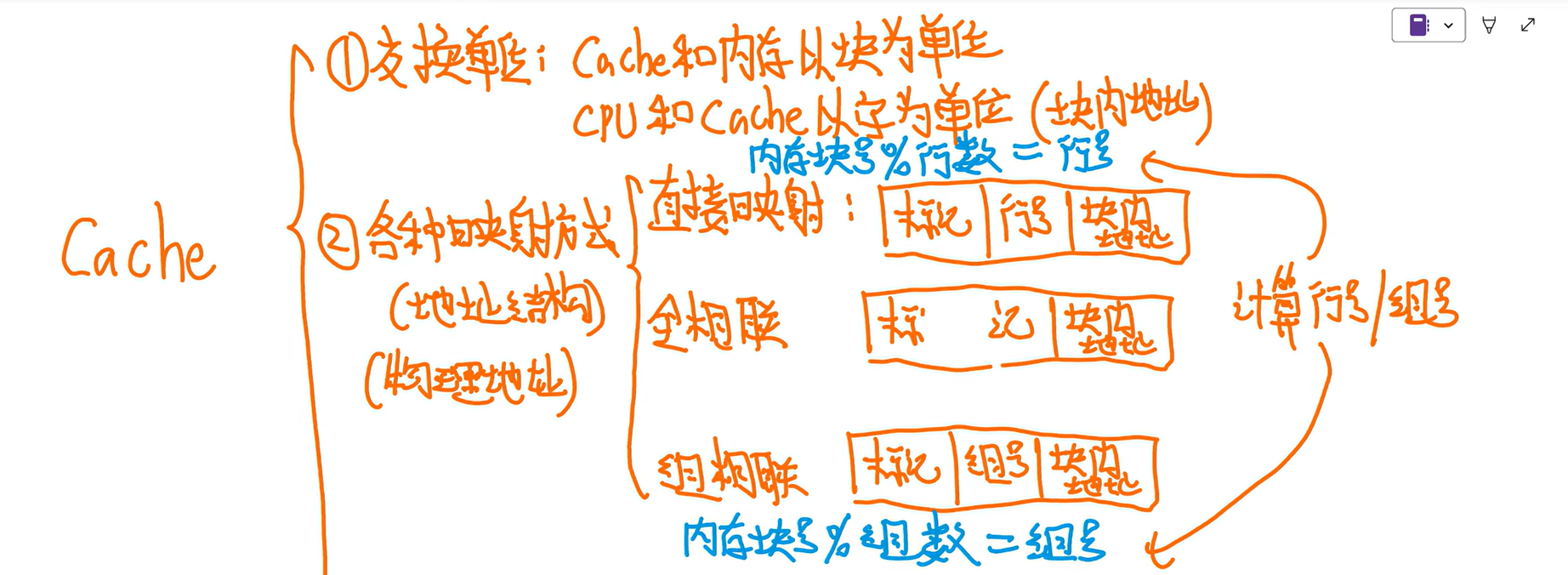
标记相等,且有效位为1(防止是旧数据,比如关机前的),才能说明cache是你想要的
Cache总容量=标记阵列=地址映射表:书p121
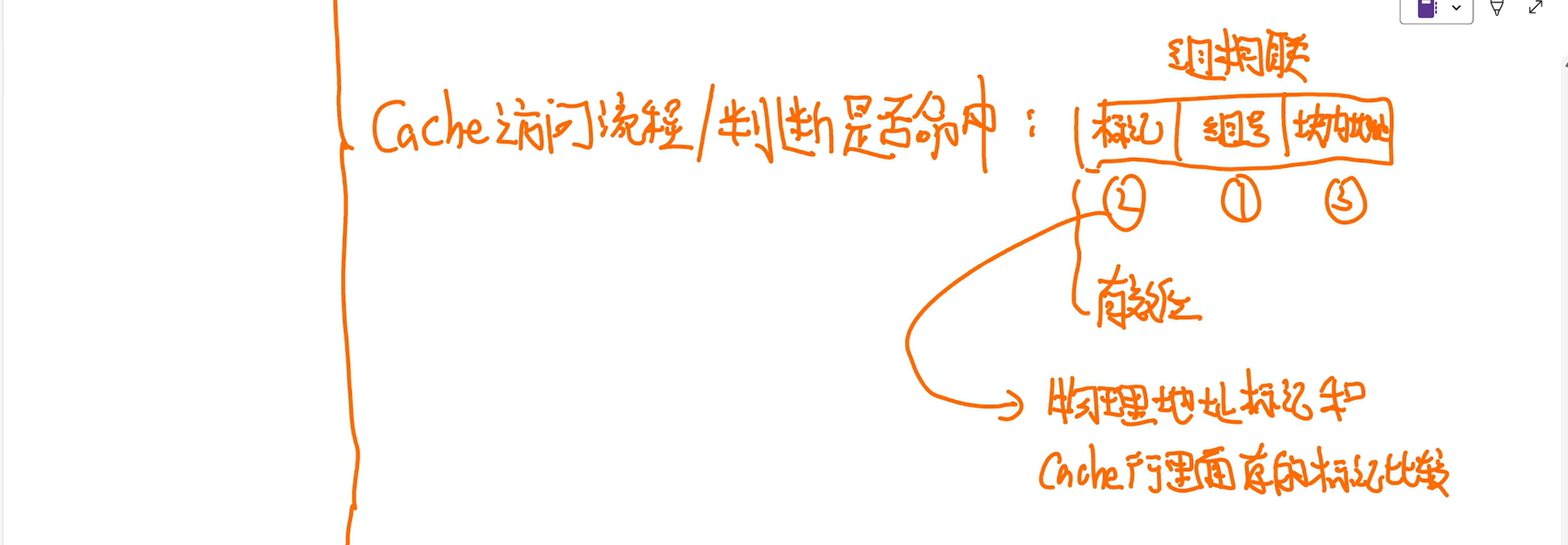
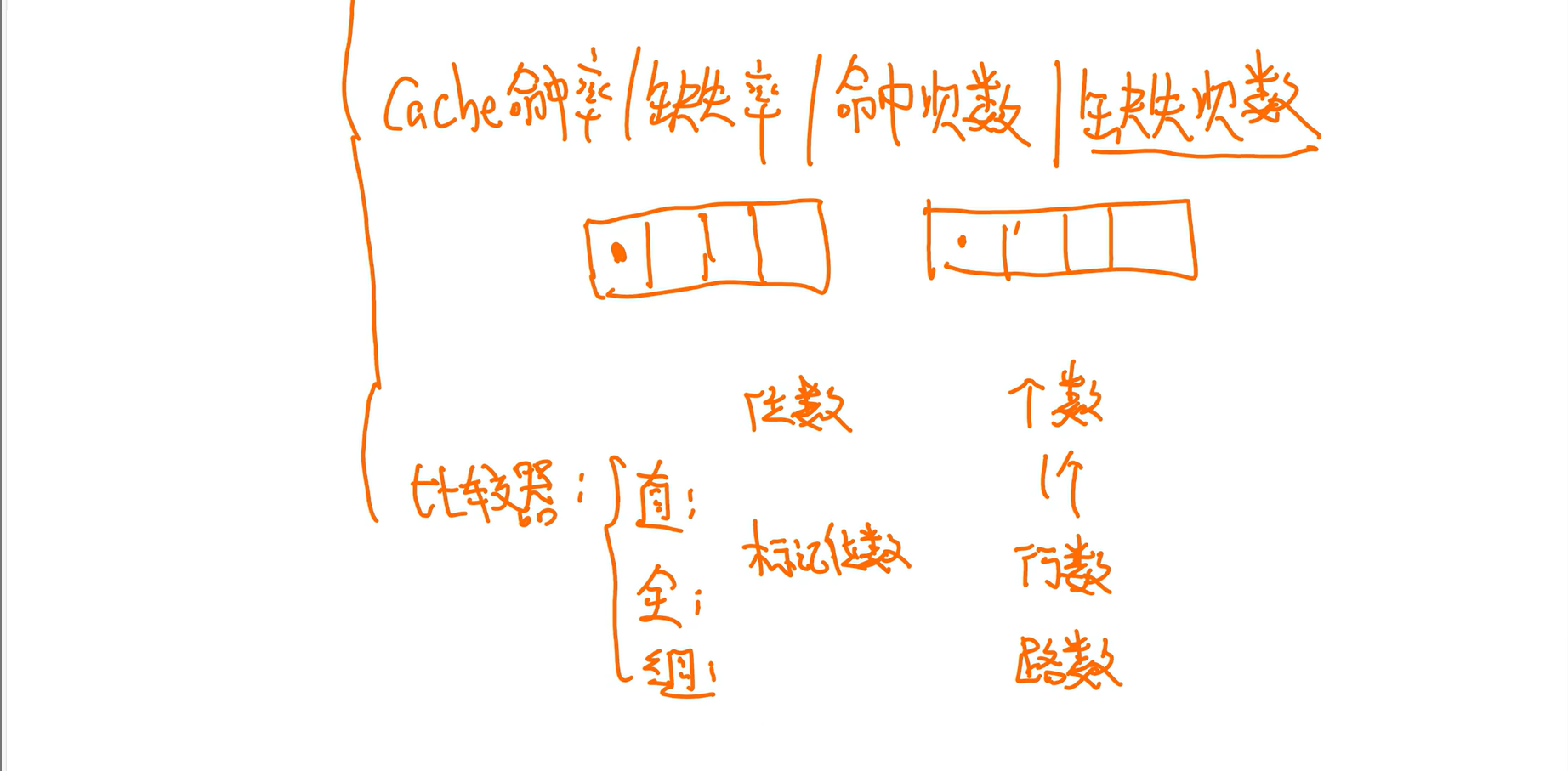
Cache访问流程和比较器在书本p119顶部
3.5课后习题
3.5.6
【例 3.3】
3)

p124
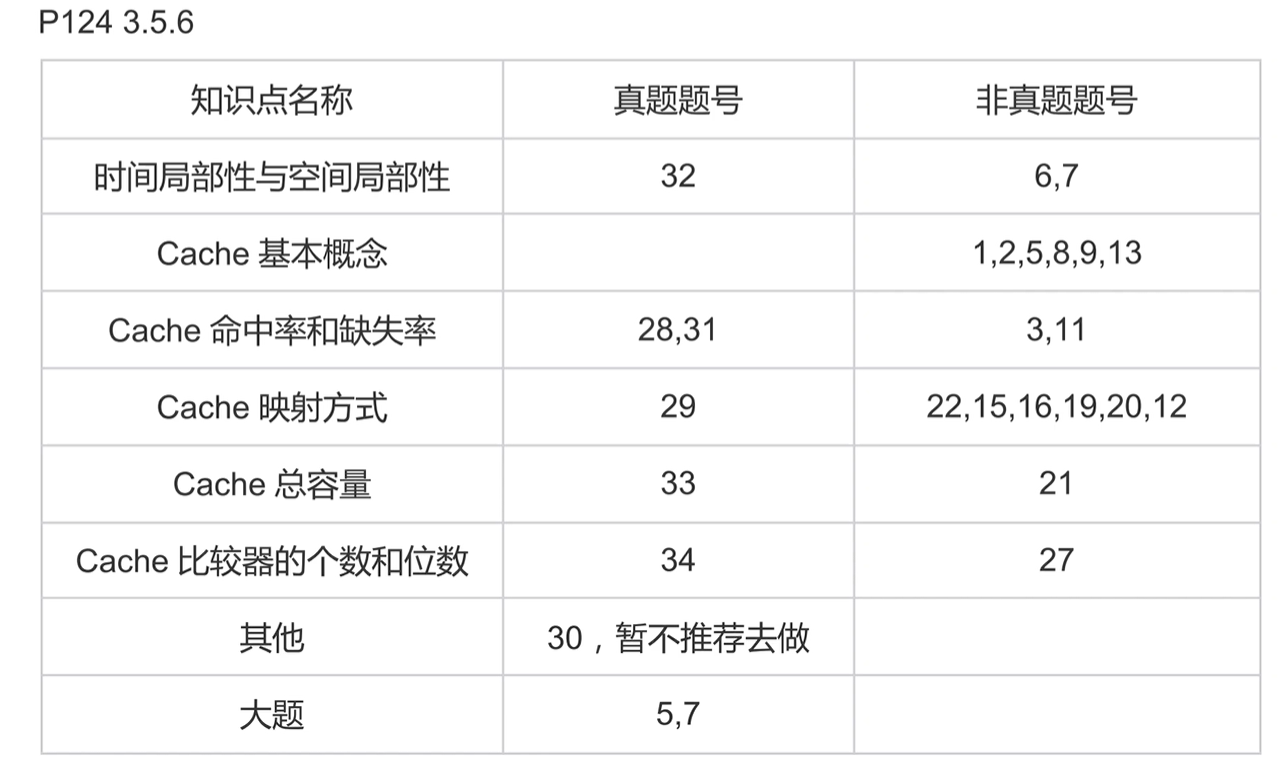
29.
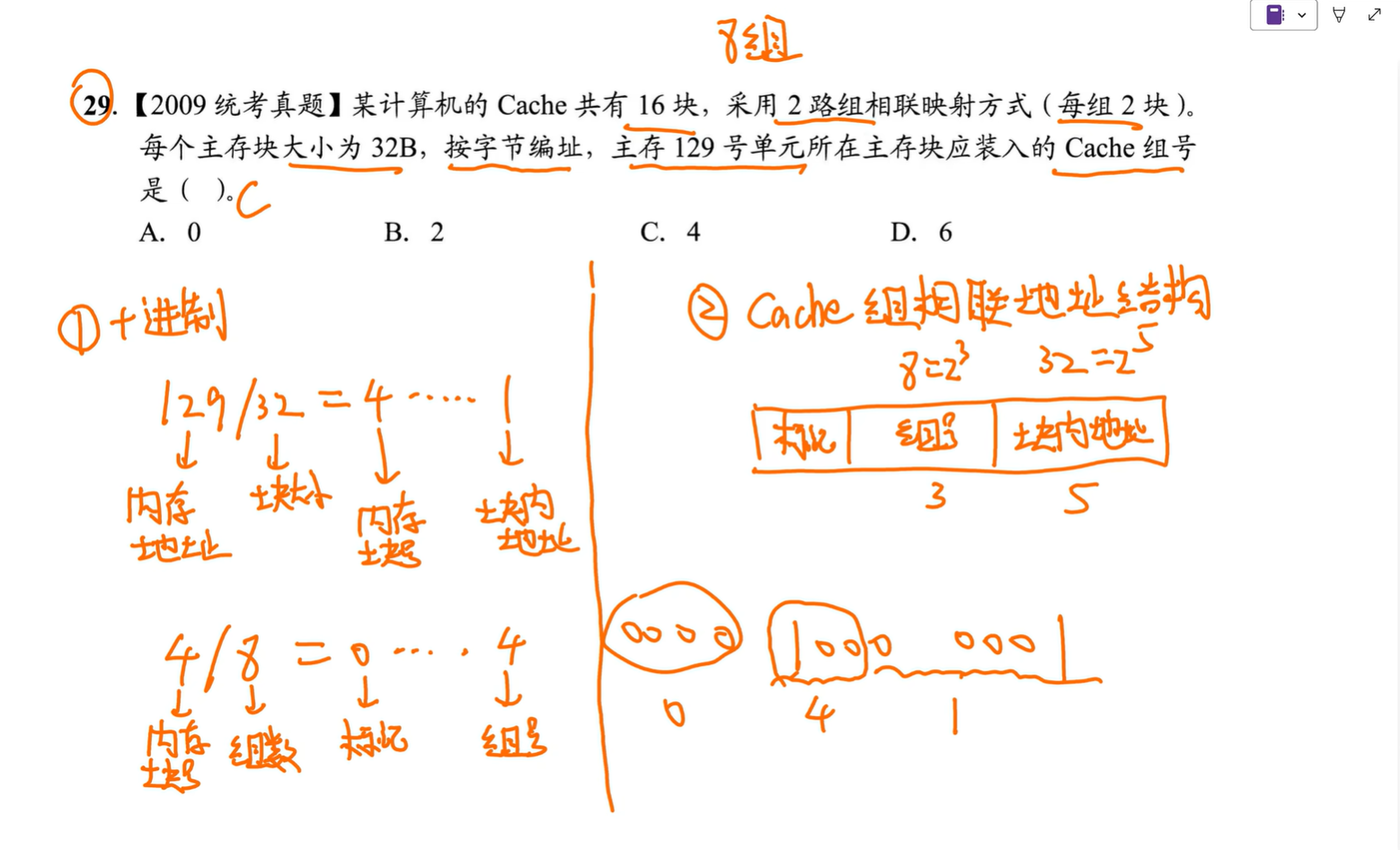
31.

代码从a[0]开始读,但是a[0]没有,所以缺失
cache以块为单位,一块4个数据(块大小16B/一个数据占4B),最开始cache为空,找不到第一个数据,就会把整个块16B导入
这里对每个cache块进行读+写,第一个元素读的时候缺失了,把整个cache块放进来,写的时候就不会缺失
这种题目的做法:看一个cache块能放几个数据,一般第一个缺失;再看读/写几次
如果问缺失次数:1000×2×1/8(总次数/缺失率)0
第4章 指令系统
指令系统
概念见书p156-160
定长操作码与扩展操作码

随着地址减少,操作码变多
指令的寻址方式
基址寻址
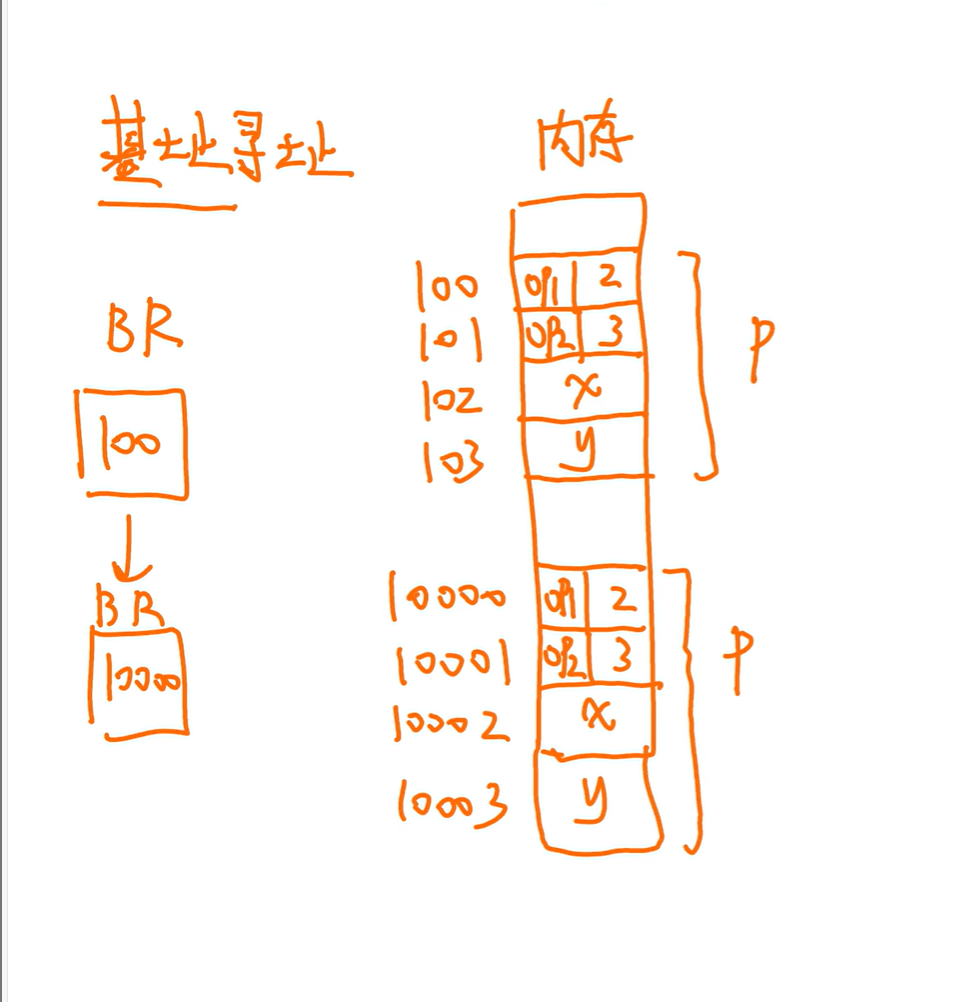
变址寻址
基址寻址 v.s. 变址寻址
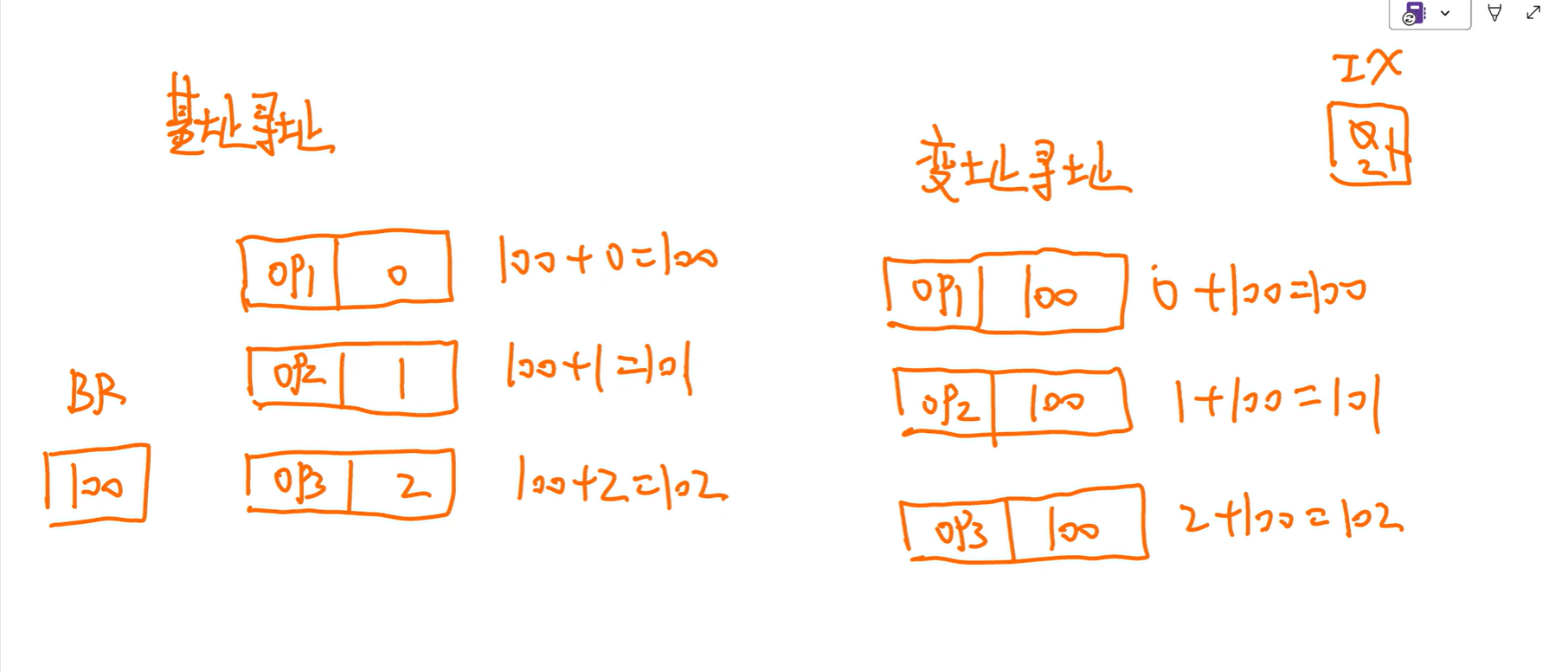
变址寻址处理数组问题
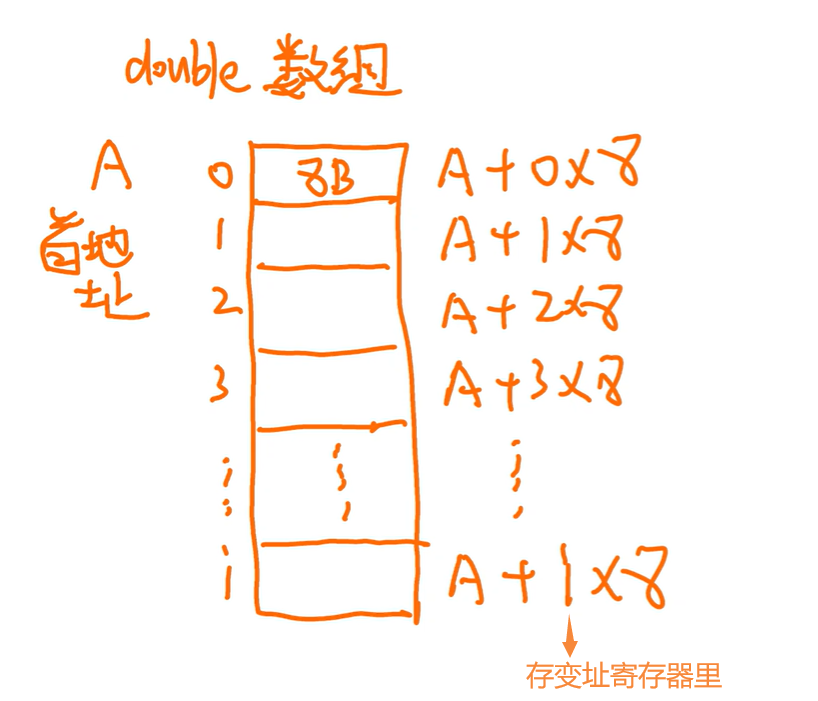
double 8字节 64位
例:书p172 32.

课后习题
27.

29.

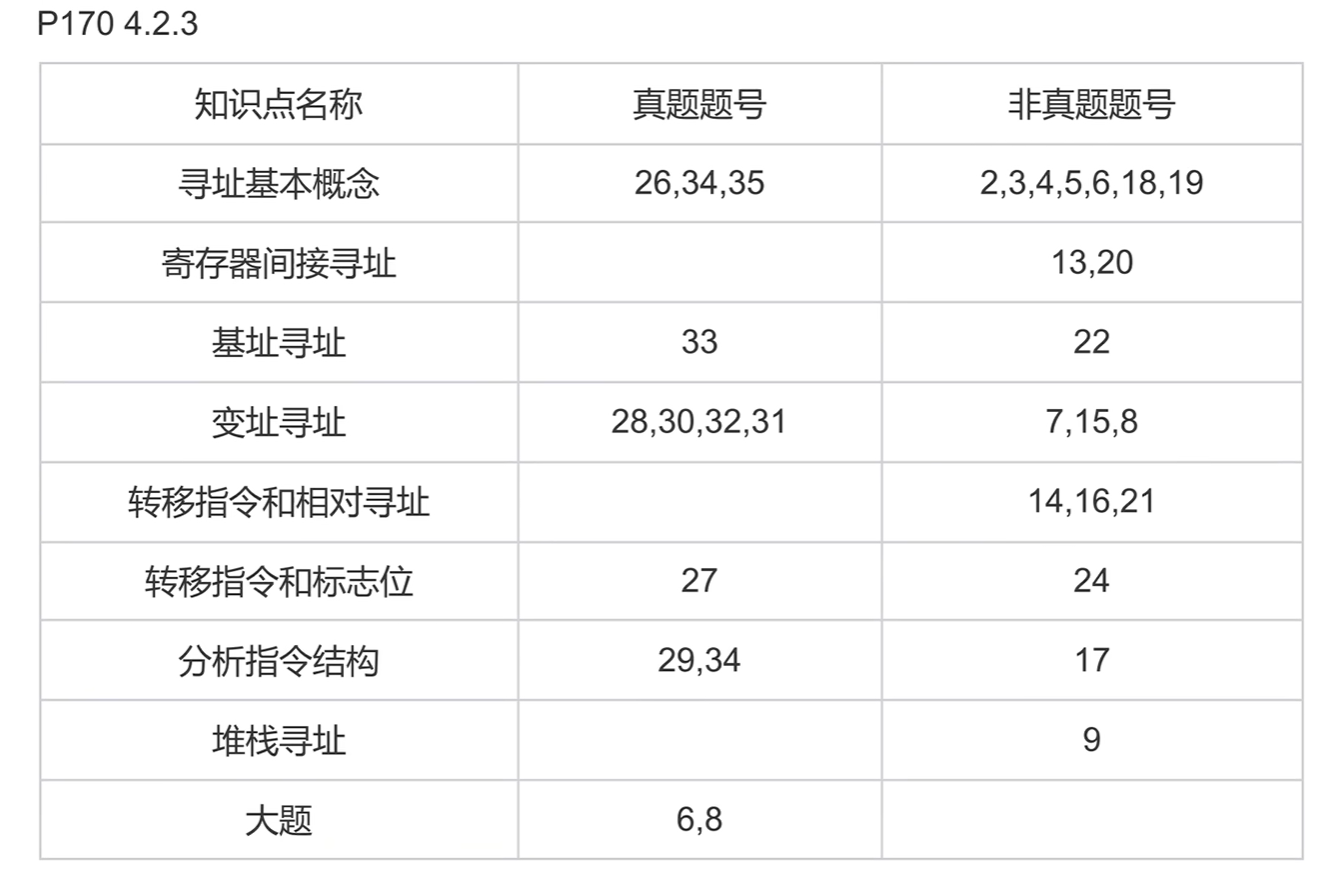
34.
如果改成间接寻址:
要看内存存储单元多大,假设是n位,寻址范围为0~$2^n-1$
如果改成相对寻址:(PC)+A,既要看A又要看PC
CISC 和 RISC 的基本概念
书p201-203
第5章 中央处理器:发哥版
CPU功能和基本架构
书p206-208
课后习题
26.
相关知识点——边界对齐:首地址是该类型大小的整数倍;整个大小是最大类型大小的整数倍
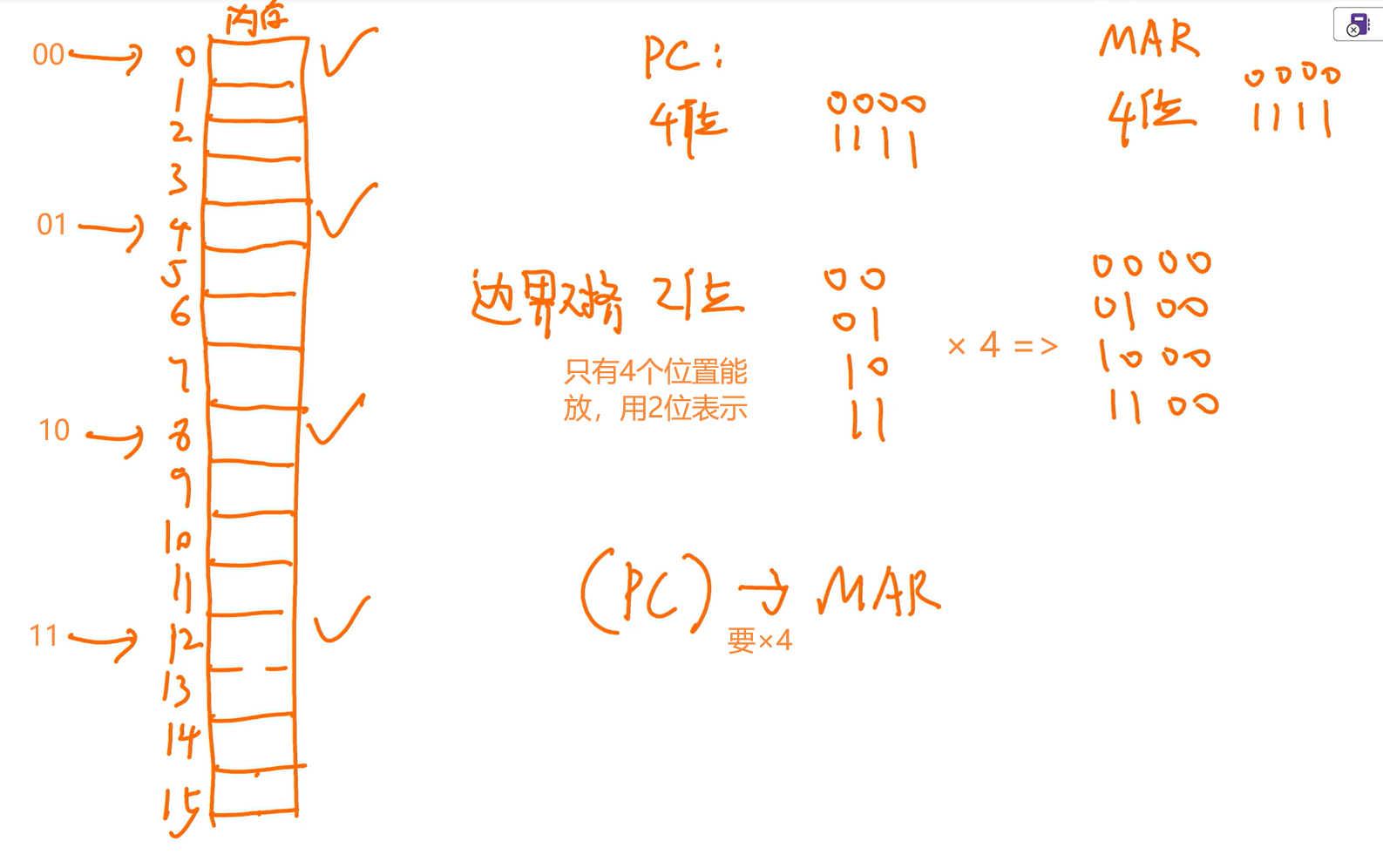
本题解答:
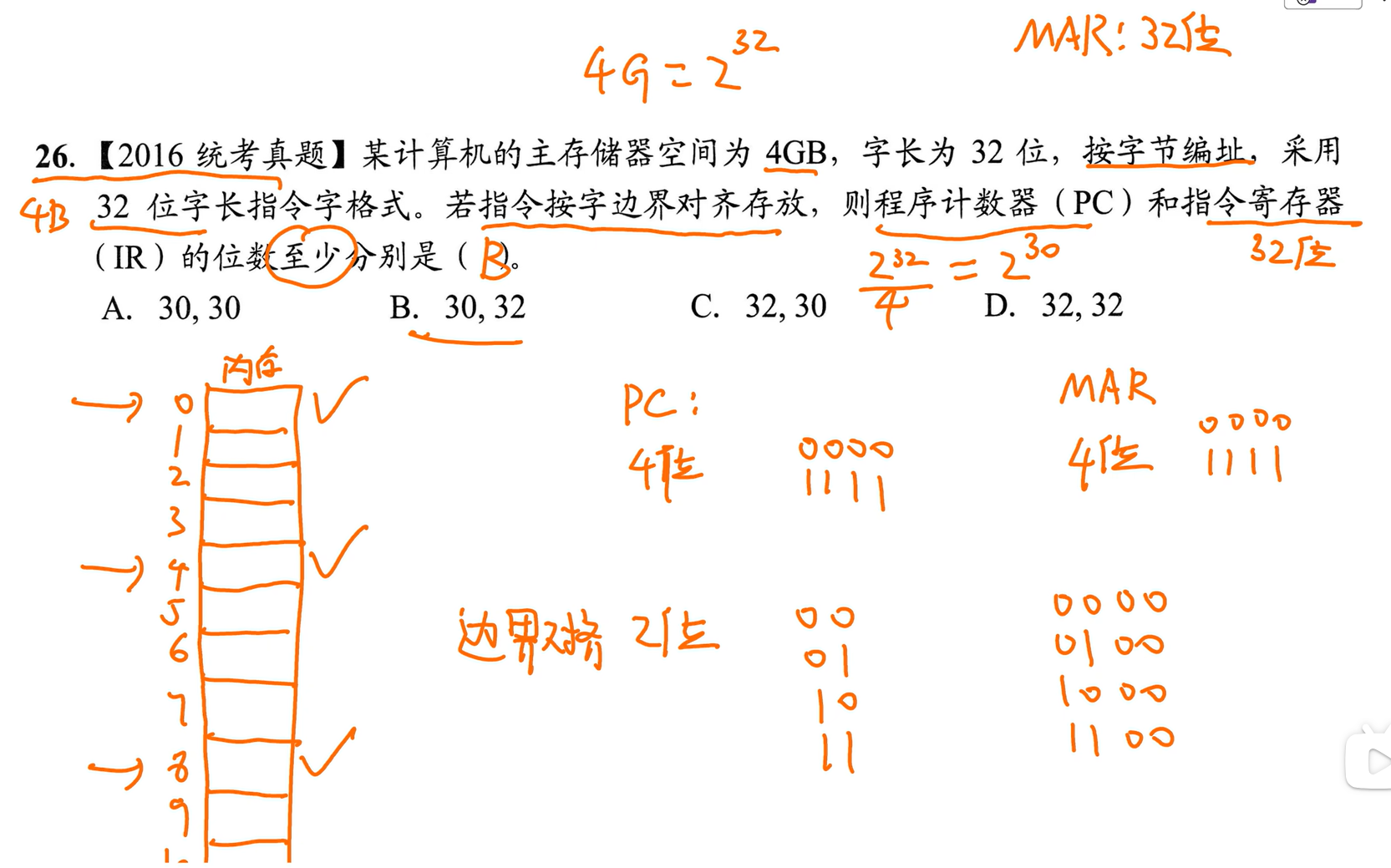
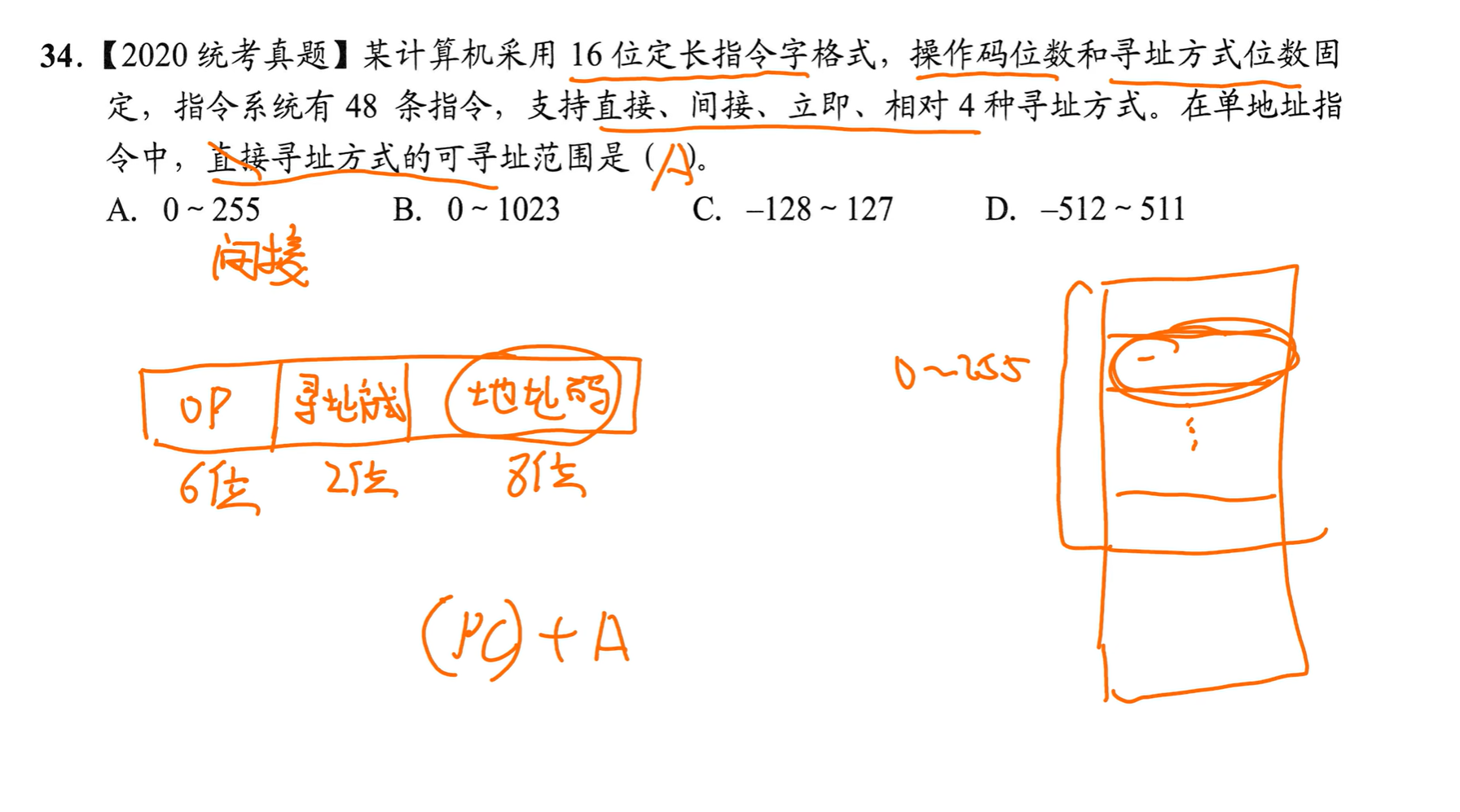
按边界对齐,PC也可以放4位,0000~1111,但很多用不到会浪费,好处是访问内存不需要变换
算PC位数:看指令能有多少个位置可以放,再取多少个2
PC位数=内存数量/一个指令占多少个地址(内存器容量/指令字长)
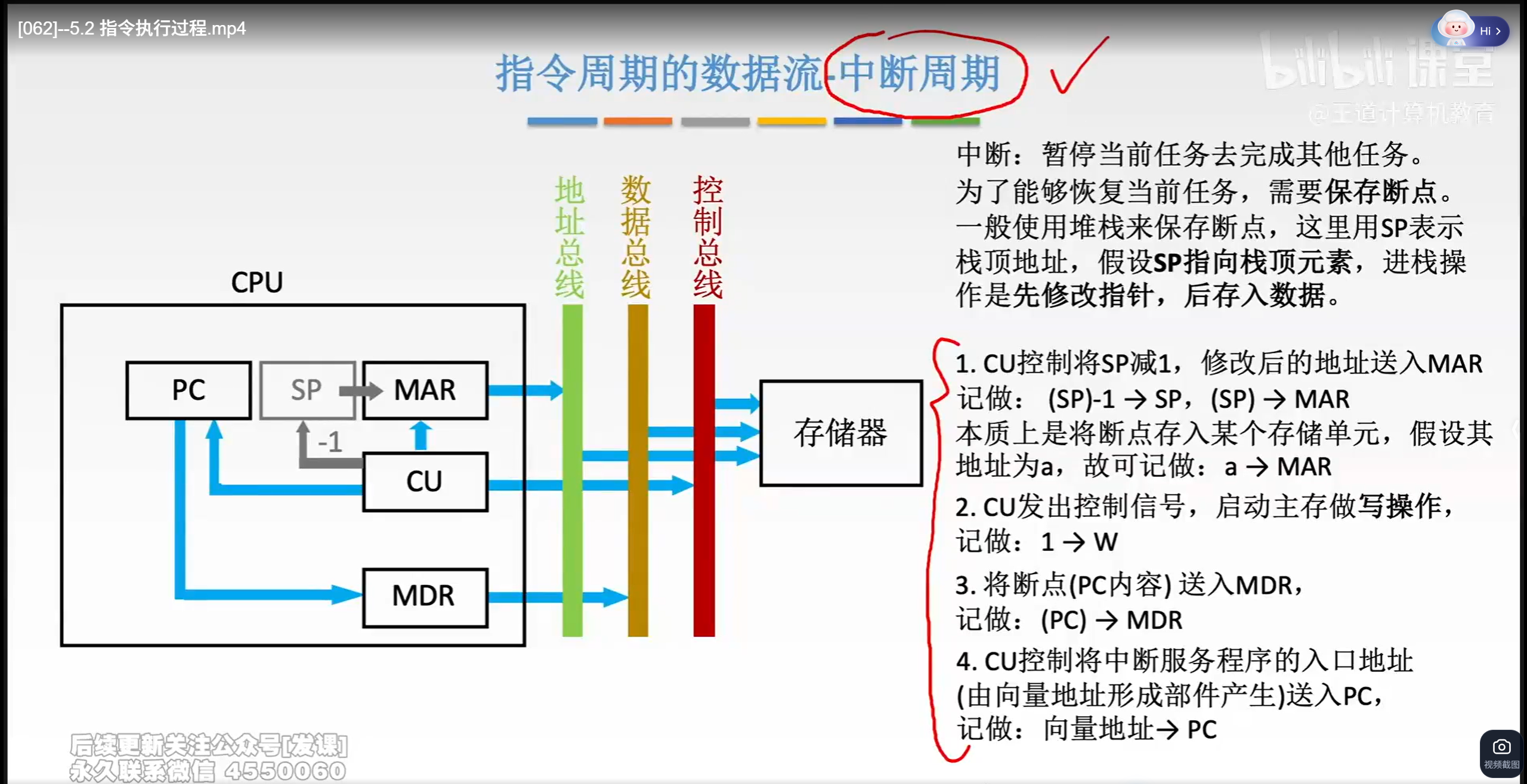
指令执行过程
p213-216
数据通路的功能和基本结构
p219-222
控制器的功能和工原理
异常和中断机制
指令流水线
概念
执行过程:p254
k级流水线执行n条指令的时间:$(k+(n-1))t$
两种理解方式,第一种:

第二种:
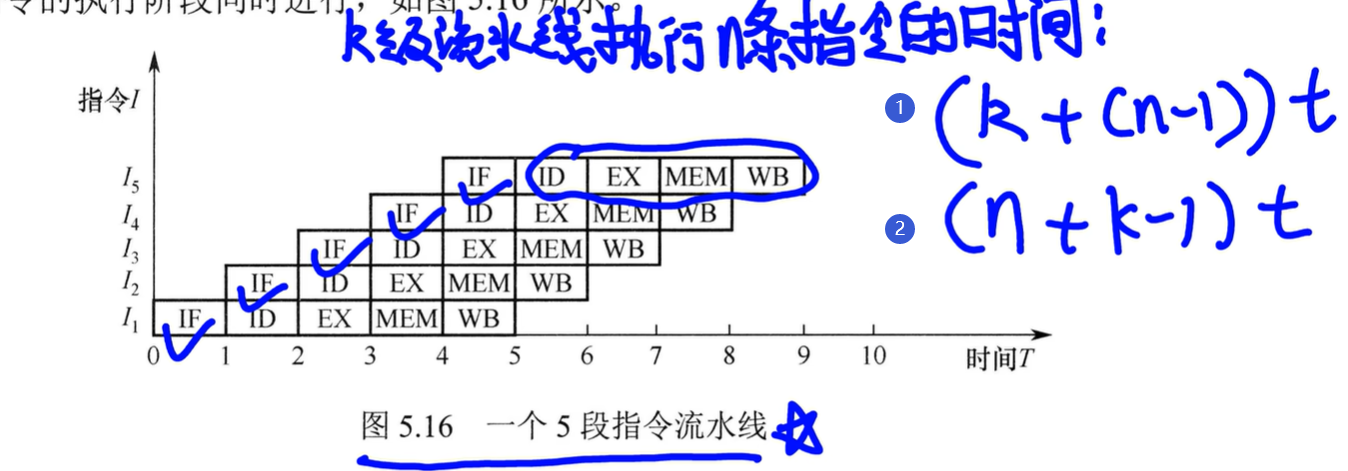
当指令足够多的时候,k->0
流水线对指令集的要求
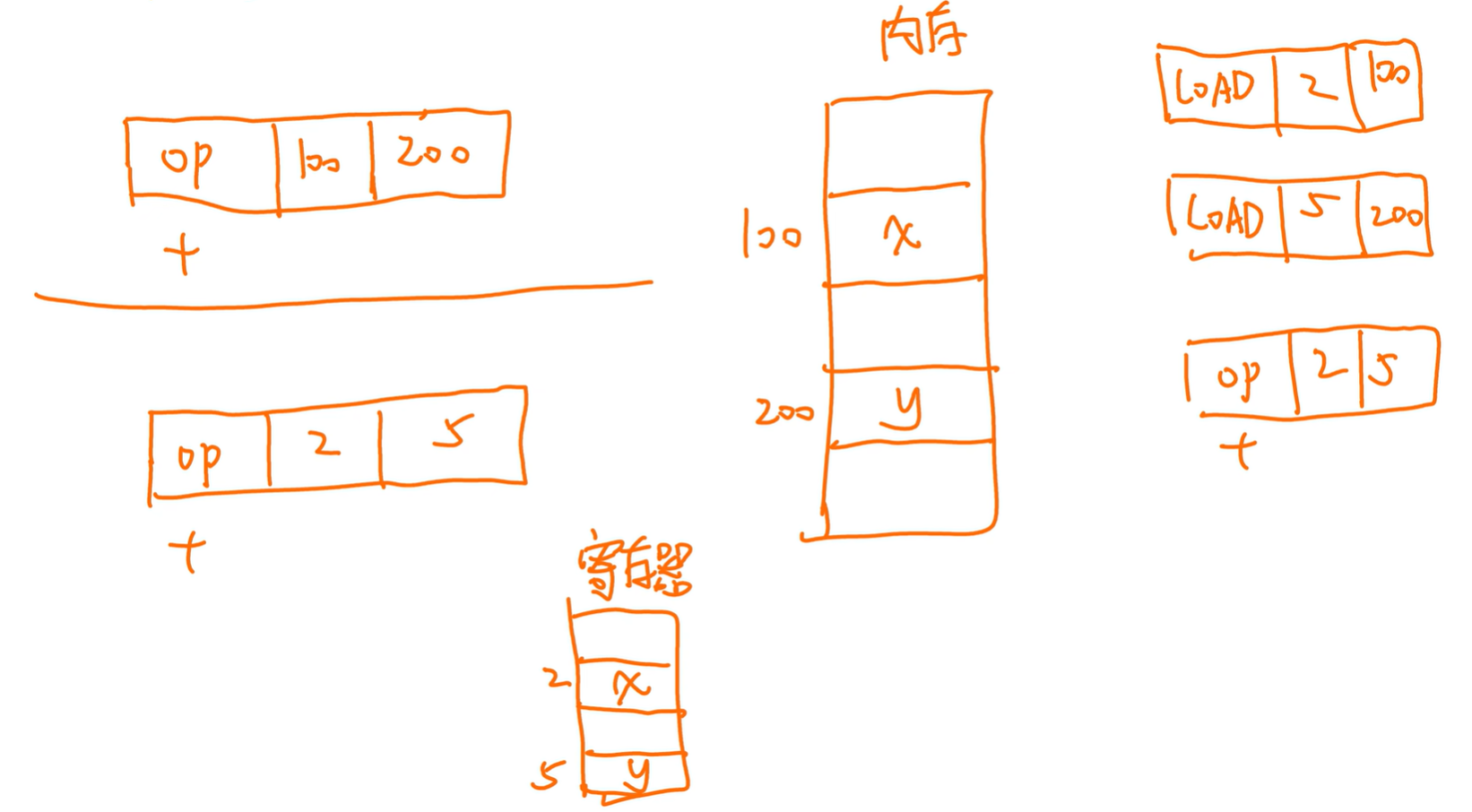
数据不用的时候先放在寄存器里
OP 100 200 拆分成三条指令:
① LOAD 2 100:100号地址的x取出来,放到2号寄存器
② LOAD 5 200:200号地址的y取出来,放到5号寄存器
③ OP 2 5:2号寄存器和5号寄存器内容相加
拆分指令可以使各条时间缩短,让各条指令时间相近
故设计时,一条指令要么访问内存,要么计算
流水线的冒险与处理
结构冒险
数据冒险
控制冒险
性能指标
吞吐量TP
加速比S
见书p259-260
习题
31.

load在MEM阶段拿到数据,下条指令的EXE应在load的MEM之后
转移指令下条的IF 要在转移指令的MEM之后
第5章 中央处理器:王道版
第6章 总线
总线概述
总线的分类

地址总线也可以作为数据通路的媒介
总线的性能指标

e.g.:

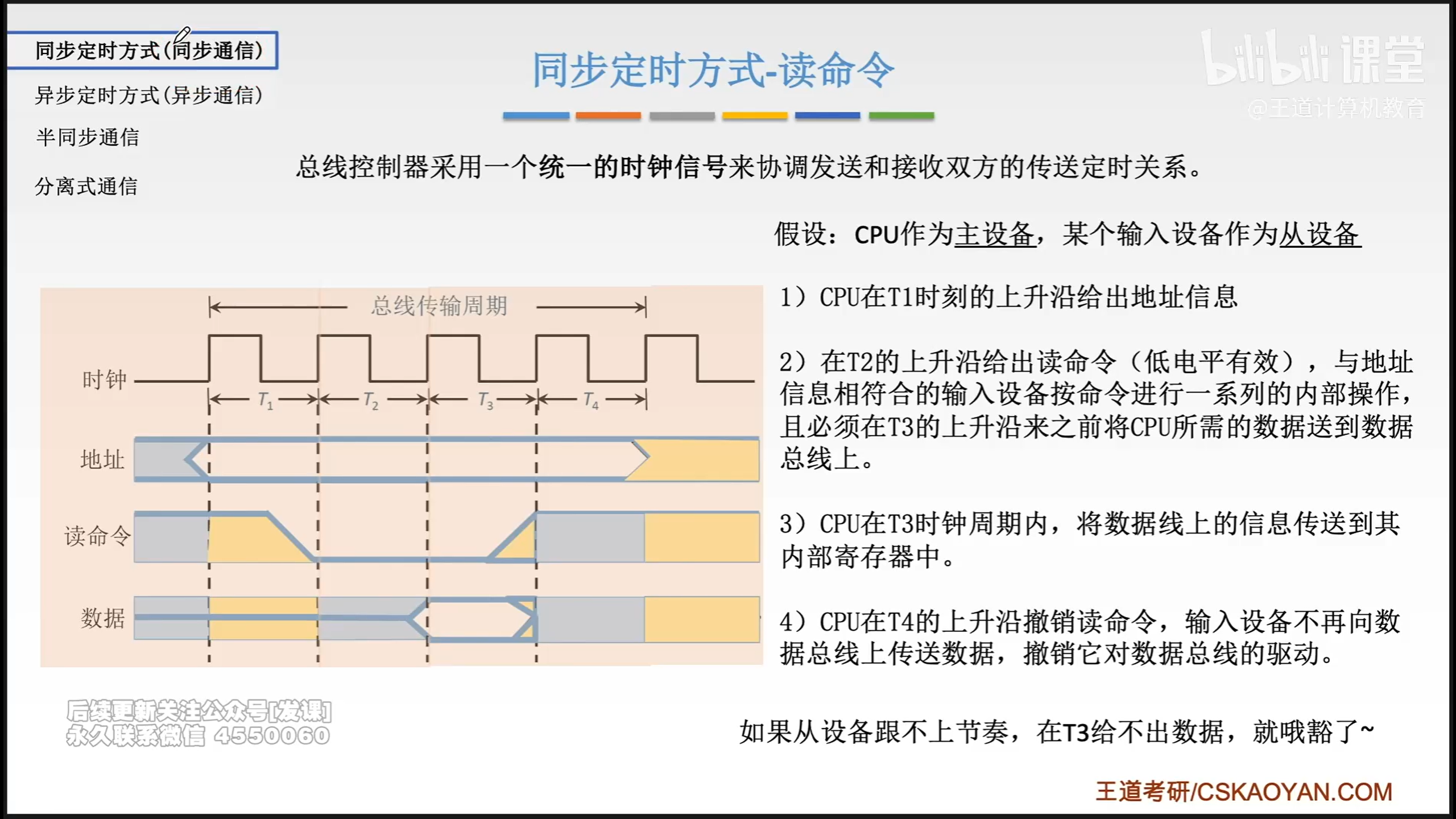
总线事务和定时
总线定时
第7章 输入/输出系统
I/O接口
I/O接口基本结构
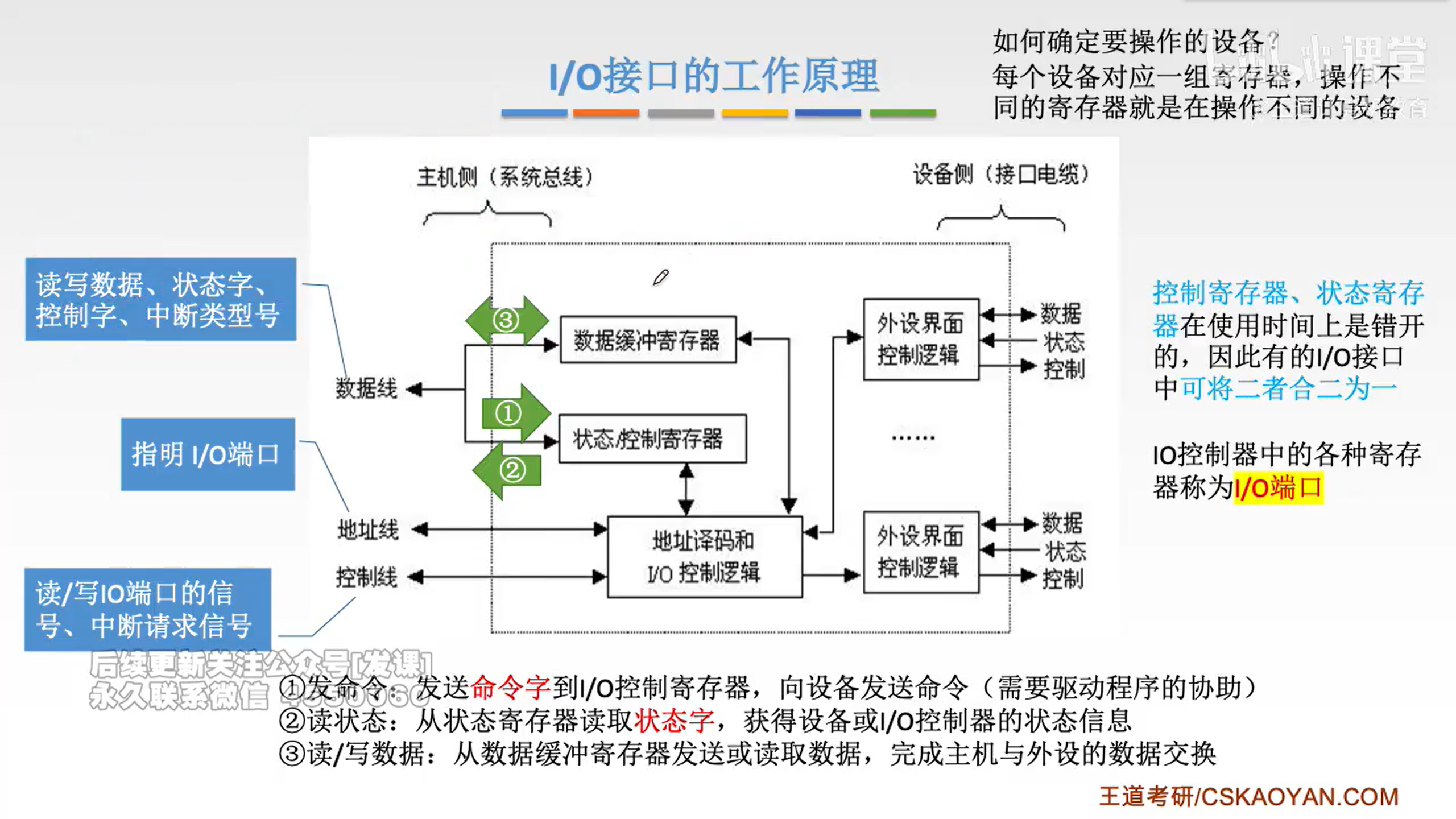
I/O端口及其编址
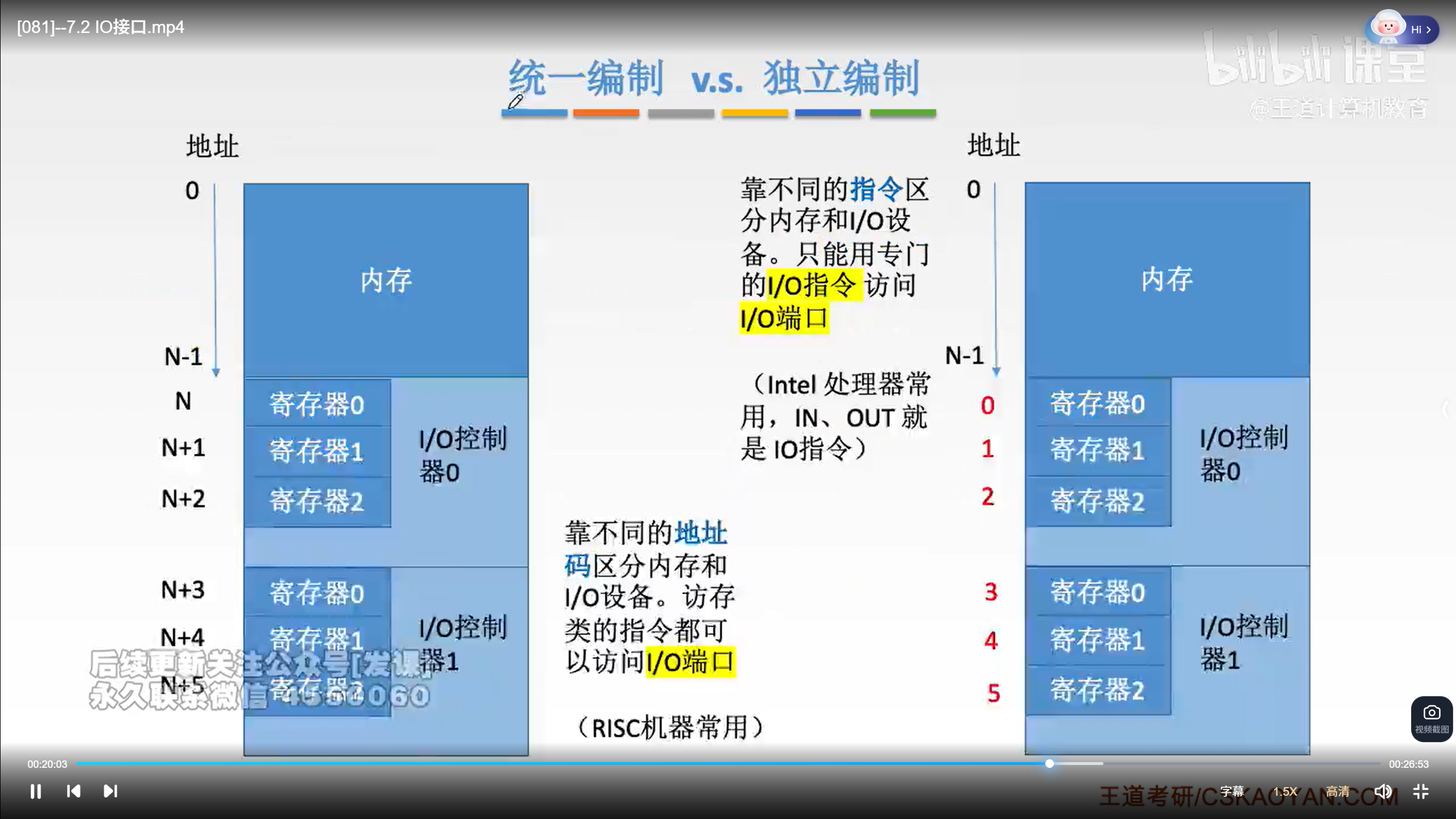
I/O方式
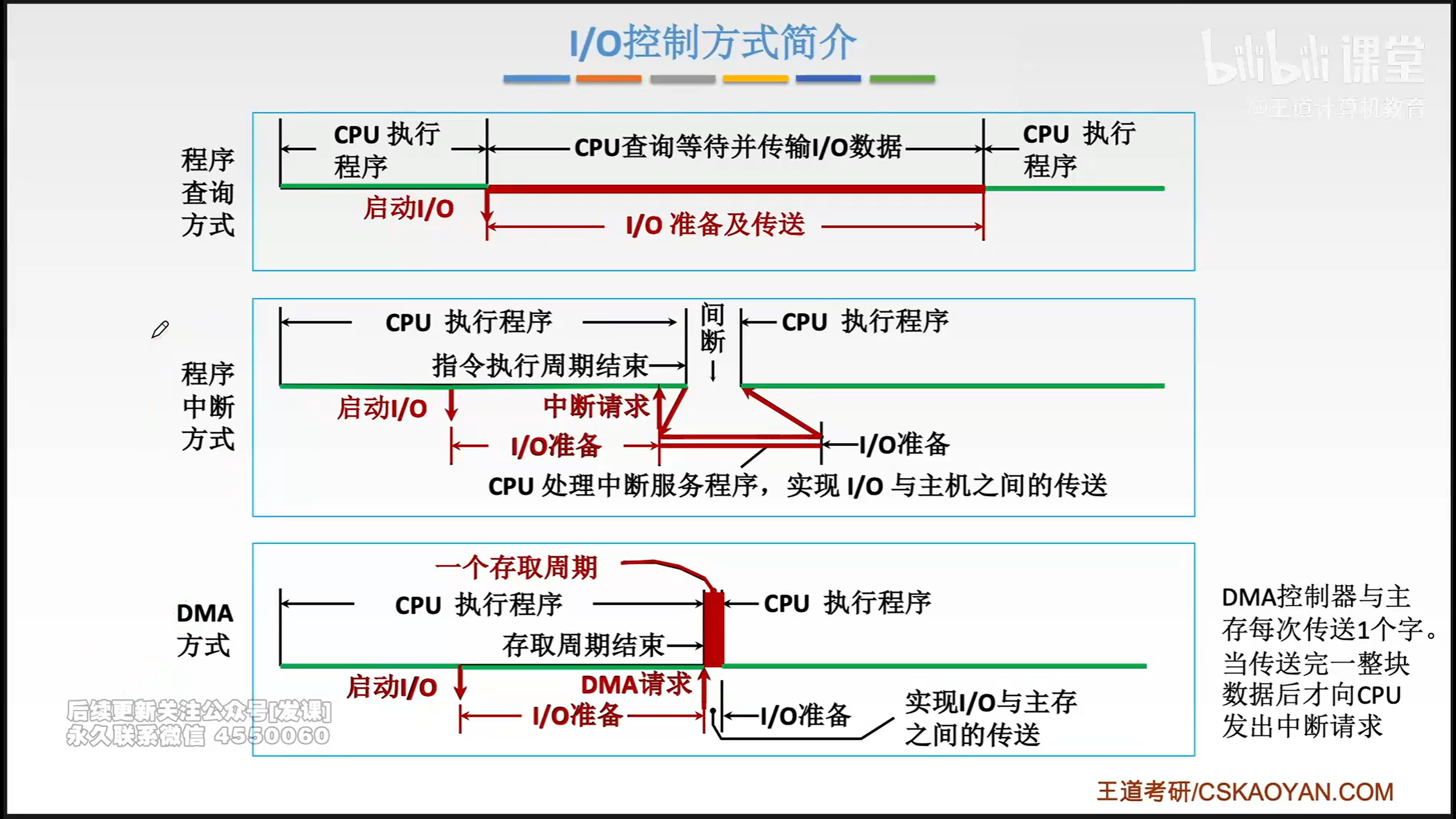
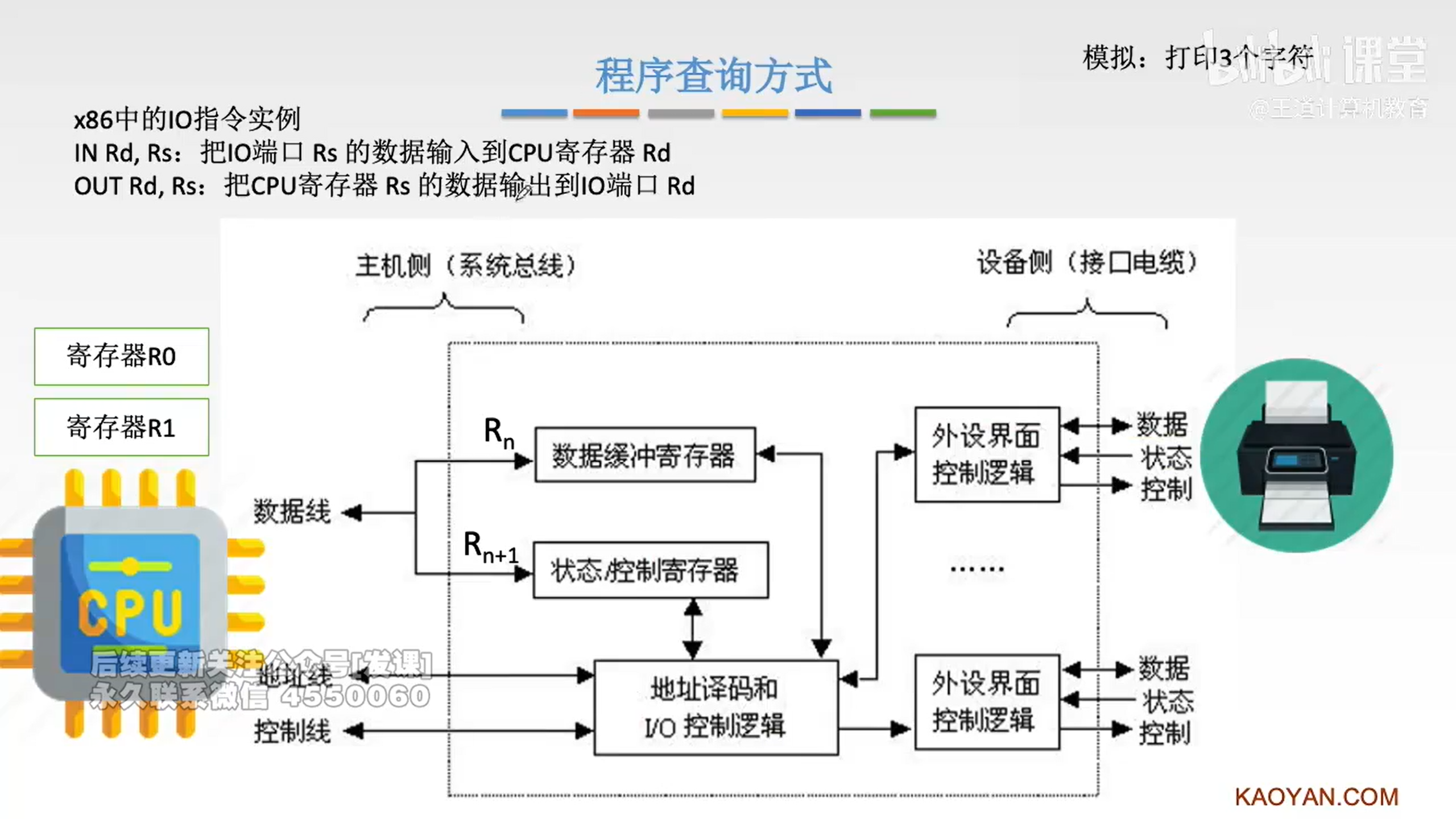
程序查询方式
查询方式示例:
例题:

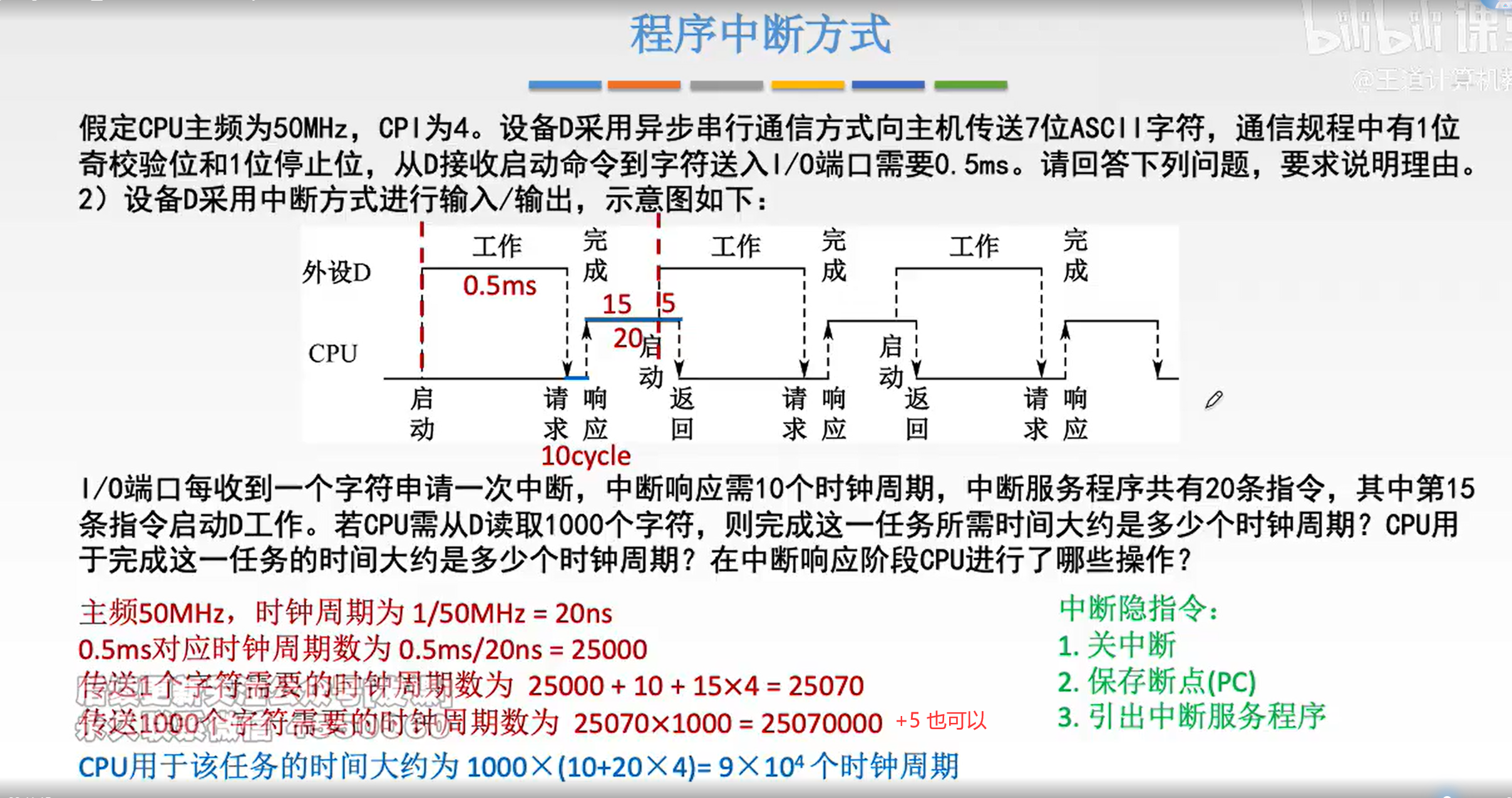
程序中断方式
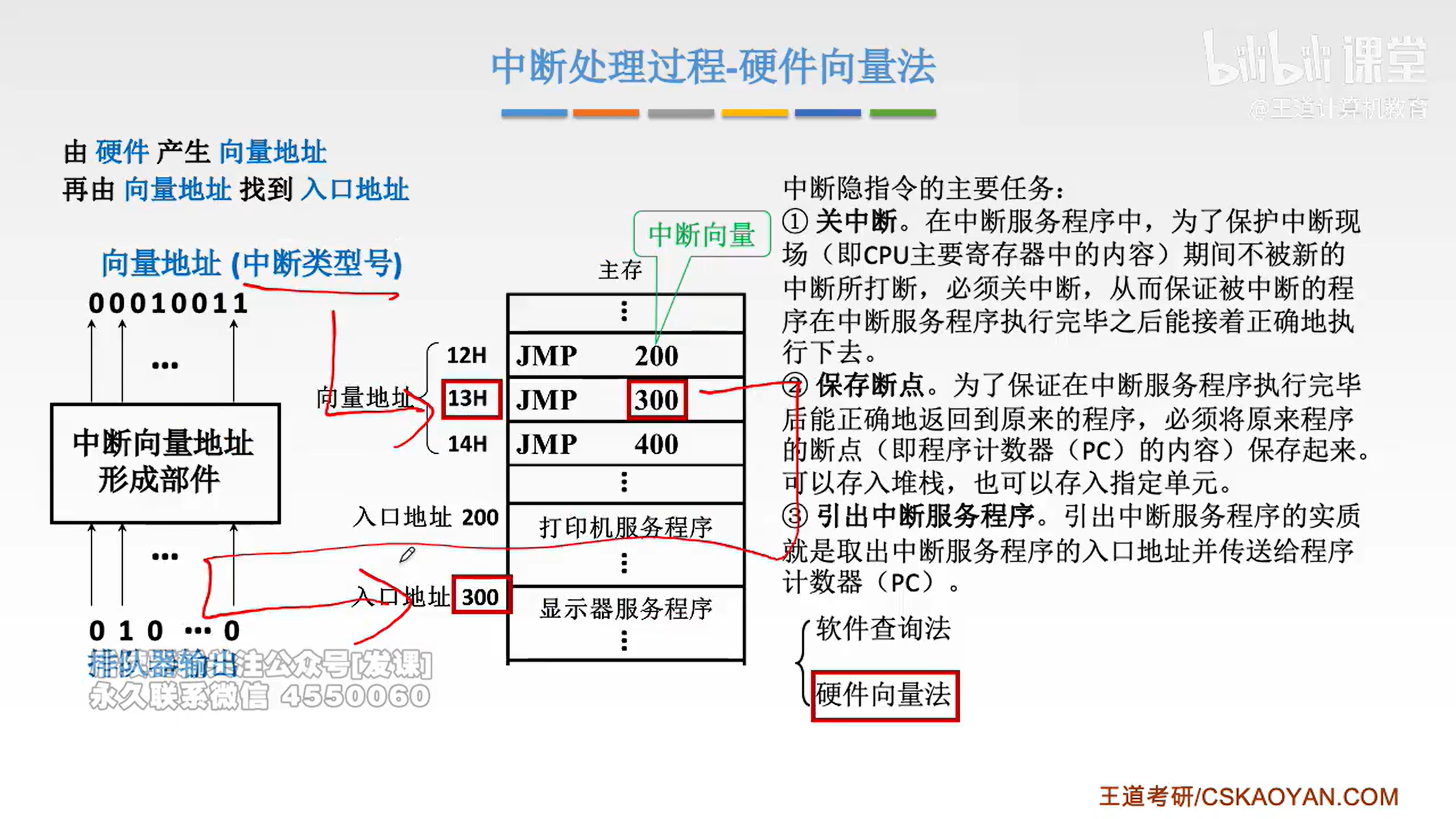
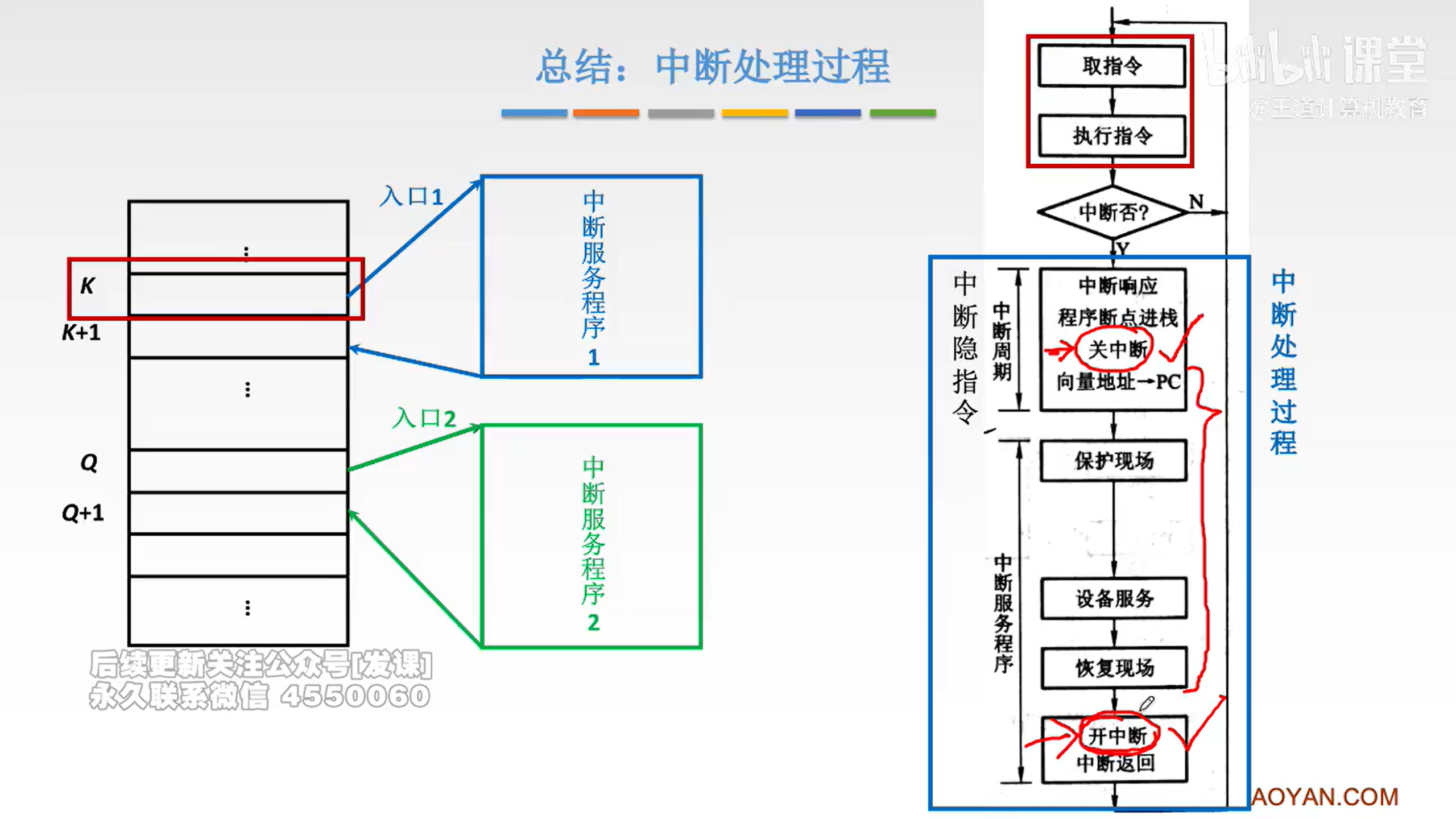
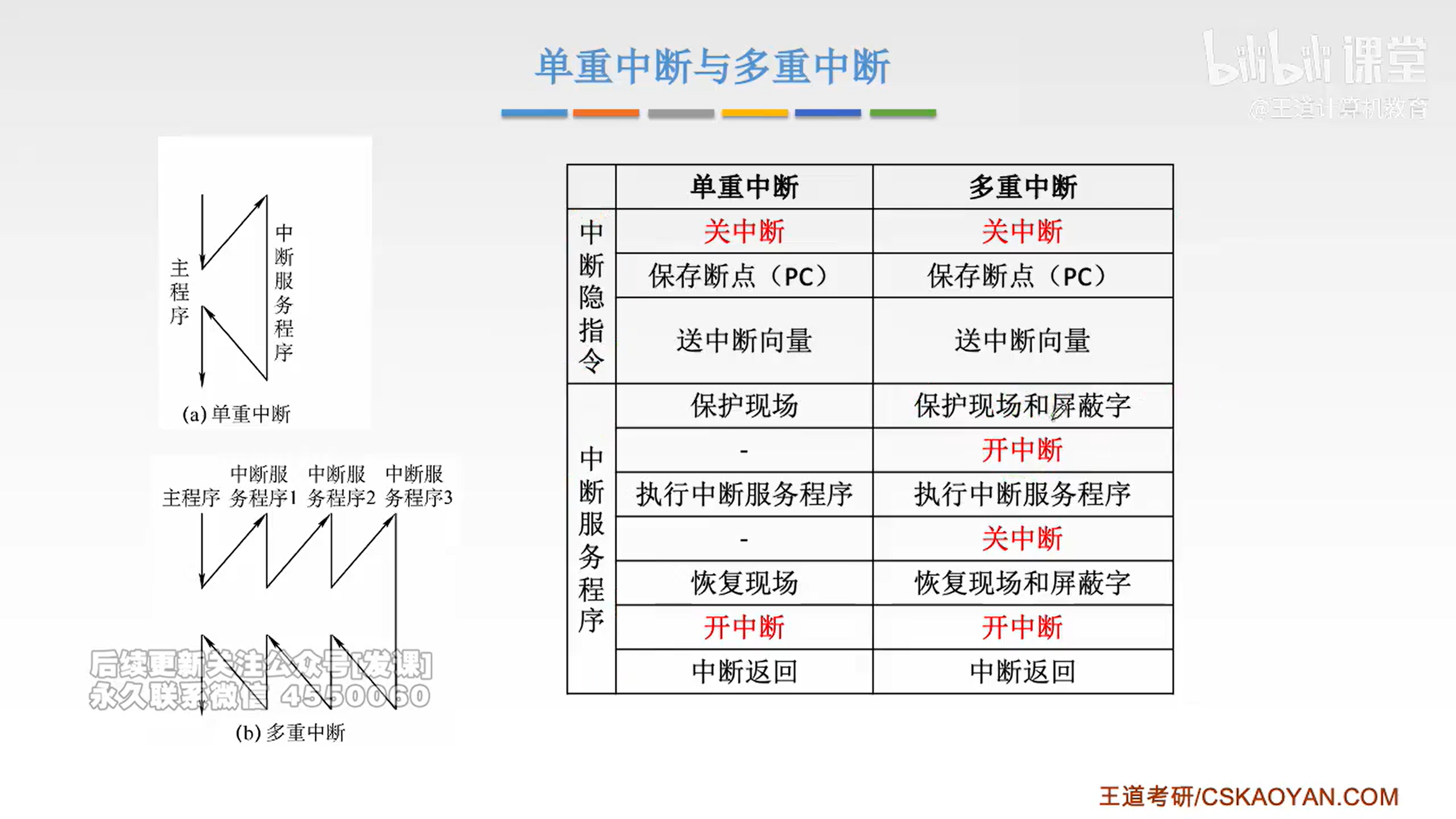
e.g.1:
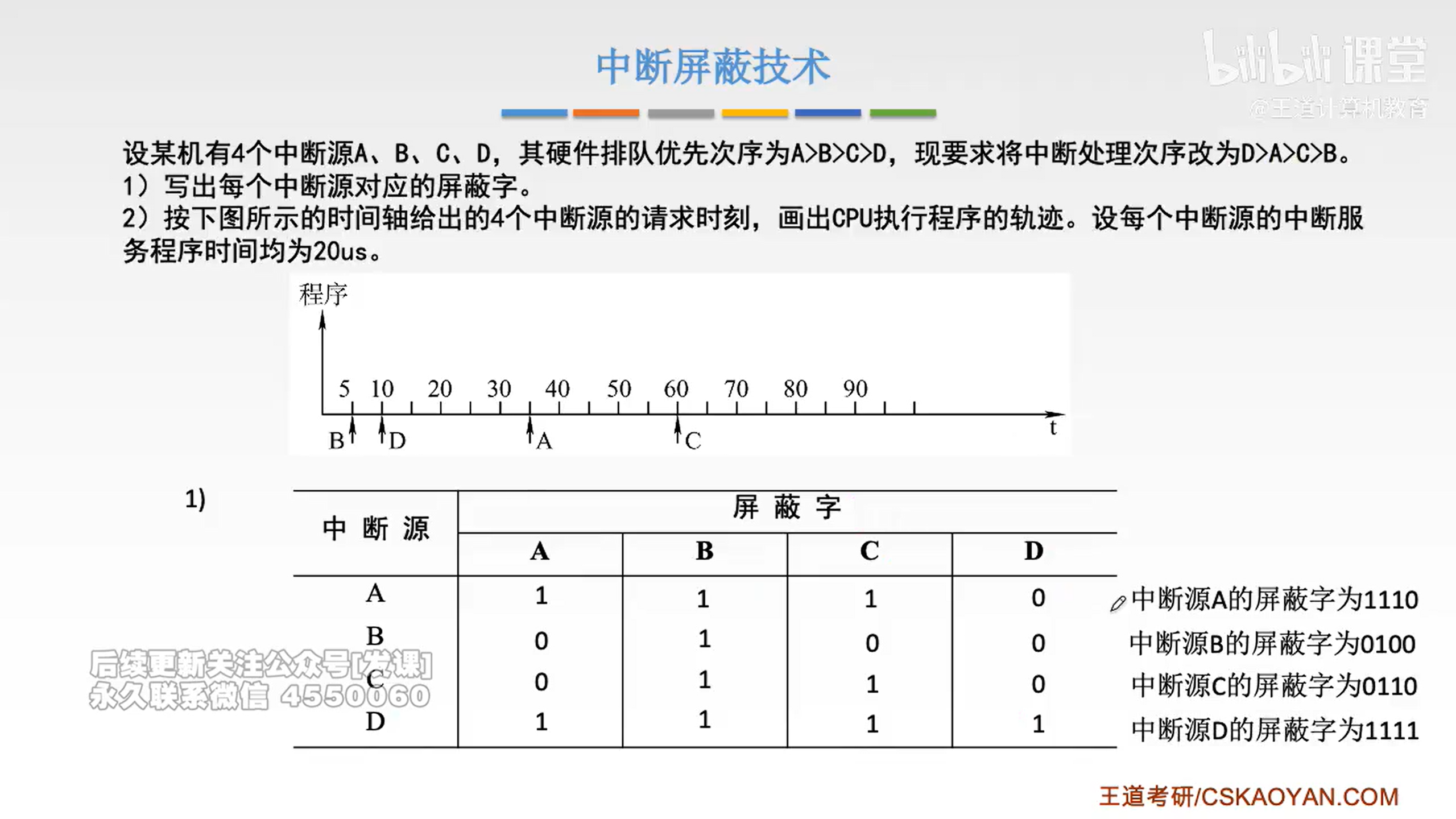
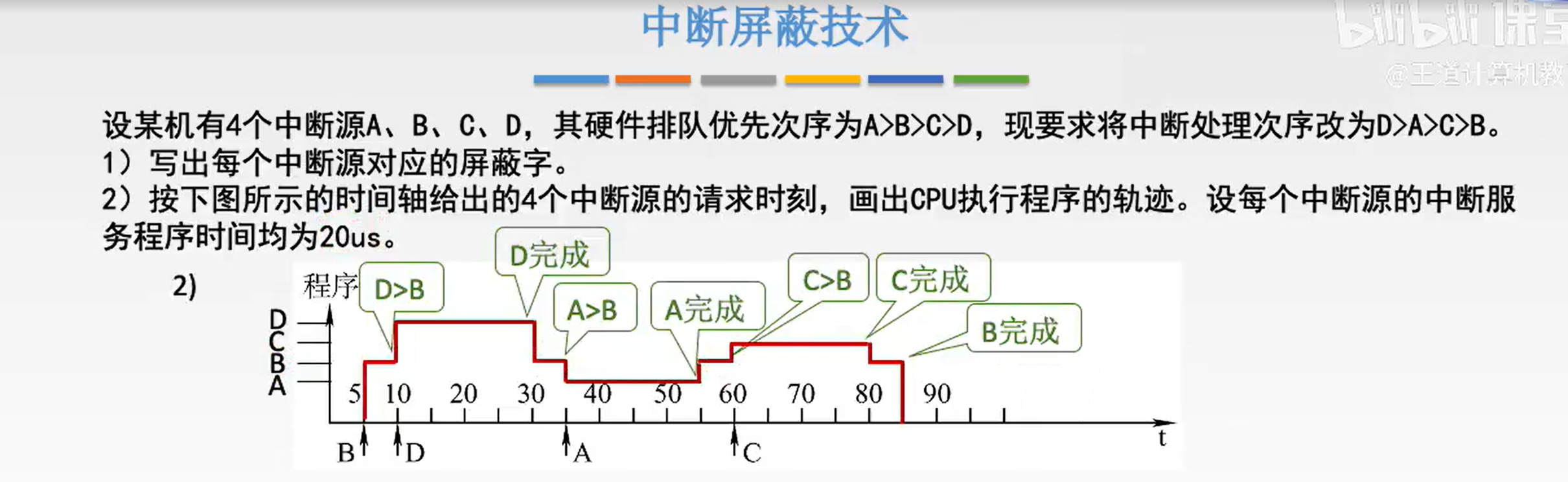
e.g.2:
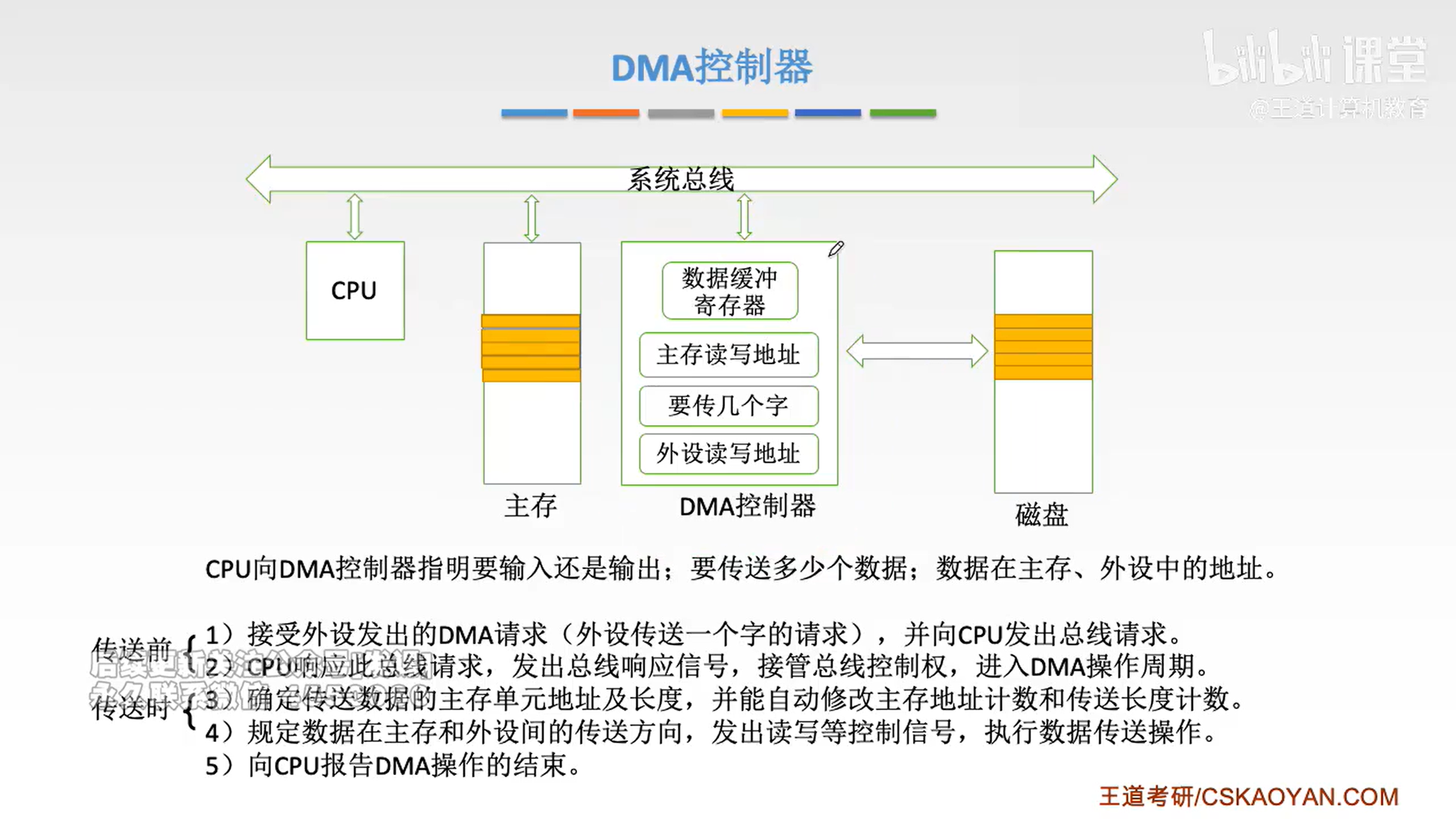
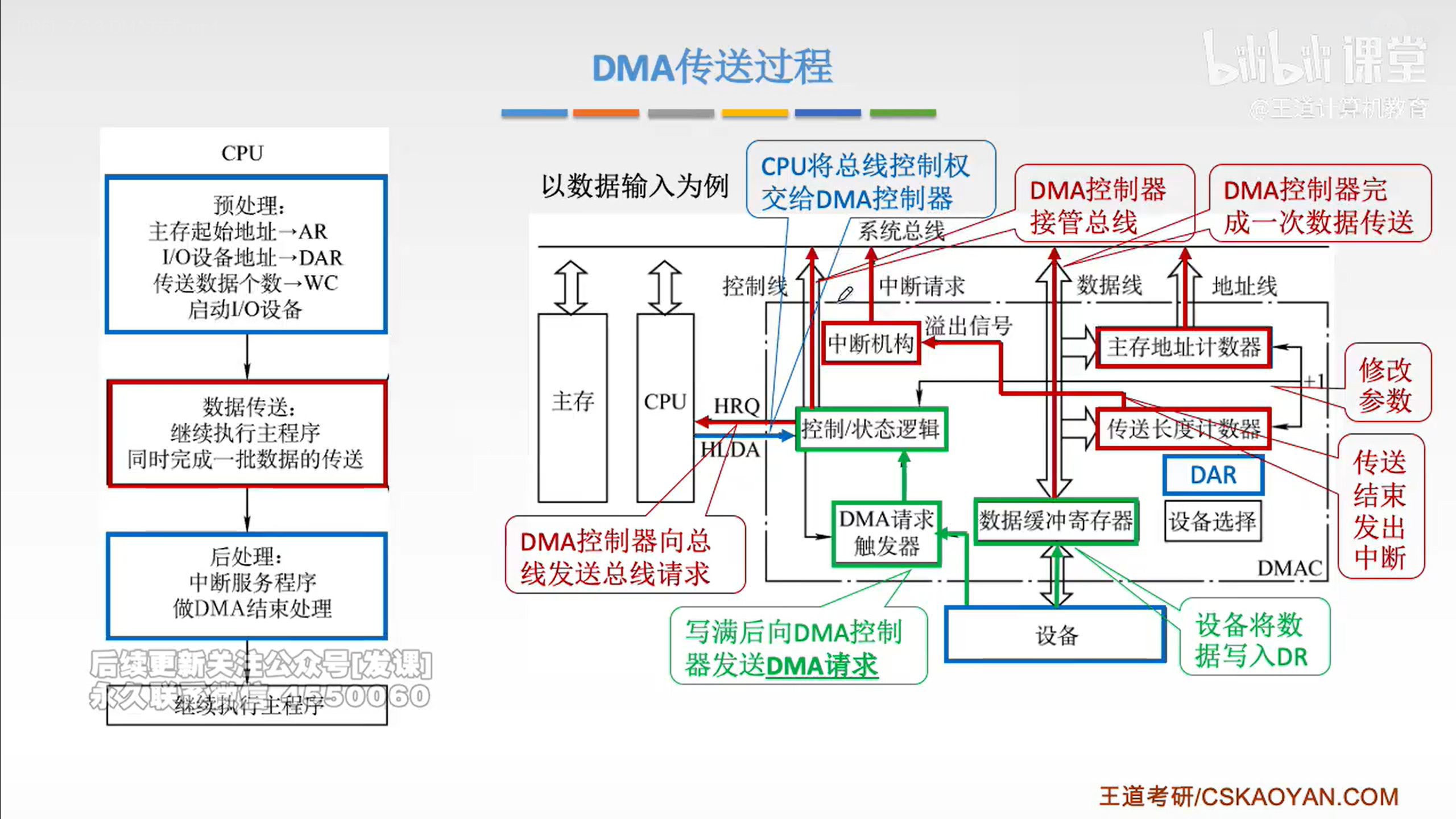
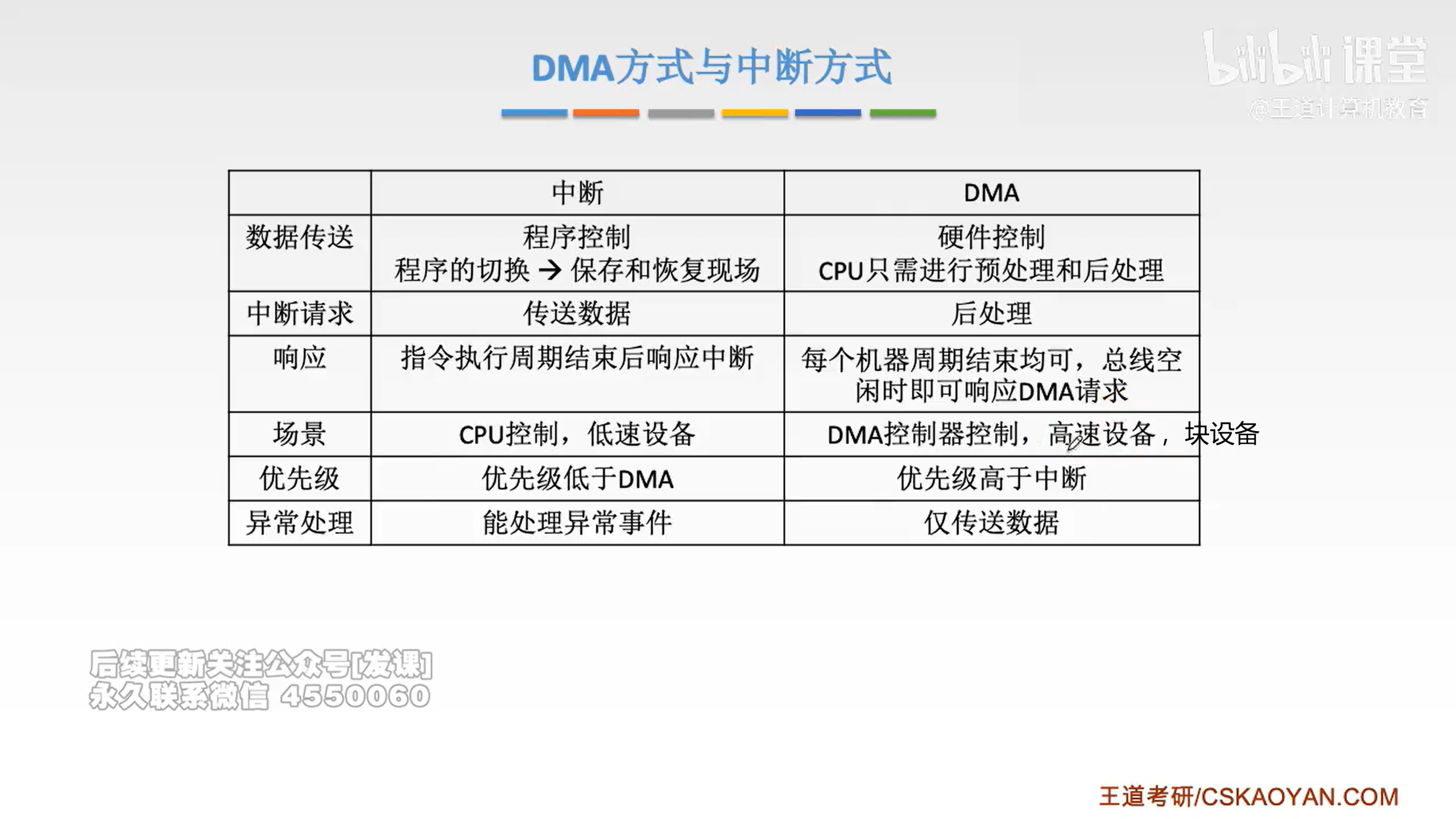
DMA方式